Data-Driven Learning of Two-Stage Beamformers in Passive IRS-Assisted Systems with Inexact Oracles

We develop an efficient data-driven and model-free unsupervised learning algorithm for achieving fully passive intelligent reflective surface (IRS)-assisted optimal short/long-term beamforming in wireless communication networks. The proposed algorithm is based on a zeroth-order stochastic gradient ascent methodology, suitable for tackling two-stage stochastic nonconvex optimization problems with continuous uncertainty and unknown (or "black-box") terms present in the objective function, via the utilization of inexact evaluation oracles. We showcase that the algorithm can operate under realistic and general assumptions, and establish its convergence rate close to some stationary point of the associated two-stage (i.e., short/long-term) problem, particularly in cases where the second-stage (i.e., short-term) beamforming problem (e.g., transmit precoding) is solved inexactly using an arbitrary (inexact) oracle. The proposed algorithm is applicable on a wide variety of IRS-assisted optimal beamforming settings, while also being able to operate without (cascaded) channel model assumptions or knowledge of channel statistics, and over arbitrary IRS physical configurations; thus, no active sensing capability at the IRS(s) is needed. Our algorithm is numerically demonstrated to be very effective in a range of experiments pertaining to a well-studied MISO downlink model, including scenarios demanding physical IRS tuning (e.g., directly through varactor capacitances), even in large-scale regimes.

Compatible Gradient Approximations for Actor-Critic Algorithms

Deterministic policy gradient algorithms are foundational for actor-critic methods in controlling continuous systems, yet they often encounter inaccuracies due to their dependence on the derivative of the critic's value estimates with respect to input actions. This reliance requires precise action-value gradient computations, a task that proves challenging under function approximation. We introduce an actor-critic algorithm that bypasses the need for such precision by employing a zeroth-order approximation of the action-value gradient through two-point stochastic gradient estimation within the action space. This approach provably and effectively addresses compatibility issues inherent in deterministic policy gradient schemes. Empirical results further demonstrate that our algorithm not only matches but frequently exceeds the performance of current state-of-the-art methods.

FEDSTR: Money-In AI-Out

The NOSTR is a communication protocol for the social web, based on the w3c websockets standard. Although it is still in its infancy, it is well known as a social media protocol, thousands of trusted users and multiple user interfaces, offering a unique experience and enormous capabilities. To name a few, the NOSTR applications include but are not limited to direct messaging, file sharing, audio/video streaming, collaborative writing, blogging and data processing through distributed AI directories. In this work, we propose an approach that builds upon the existing protocol structure with end goal a decentralized marketplace for federated learning and LLM training. In this proposed design there are two parties: on one side there are customers who provide a dataset that they want to use for training an AI model. On the other side, there are service providers, who receive (parts of) the dataset, train the AI model, and for a payment as an exchange, they return the optimized AI model. The decentralized and censorship resistant features of the NOSTR enable the possibility of designing a fair and open marketplace for training AI models and LLMs.

Strong Duality Relations in Nonconvex Risk-Constrained Learning

We establish strong duality relations for functional two-step compositional risk-constrained learning problems with multiple nonconvex loss functions and/or learning constraints, regardless of nonconvexity and under a minimal set of technical assumptions. Our results in particular imply zero duality gaps within the class of problems under study, both extending and improving on the state of the art in (risk-neutral) constrained learning. More specifically, we consider risk objectives/constraints which involve real-valued convex and positively homogeneous risk measures admitting dual representations with bounded risk envelopes, generalizing expectations and including popular examples, such as the conditional value-at-risk (CVaR), the mean-absolute deviation (MAD), and more generally all real-valued coherent risk measures on integrable losses as special cases. Our results are based on recent advances in risk-constrained nonconvex programming in infinite dimensions, which rely on a remarkable new application of J. J. Uhl's convexity theorem, which is an extension of A. A. Lyapunov's convexity theorem for general, infinite dimensional Banach spaces. By specializing to the risk-neutral setting, we demonstrate, for the first time, that constrained classification and regression can be treated under a unifying lens, while dispensing certain restrictive assumptions enforced in the current literature, yielding a new state-of-the-art strong duality framework for nonconvex constrained learning.

Federated Learning Under Restricted User Availability

Federated Learning (FL) is a decentralized machine learning framework that enables collaborative model training while respecting data privacy. In various applications, non-uniform availability or participation of users is unavoidable due to an adverse or stochastic environment, the latter often being uncontrollable during learning. Here, we posit a generic user selection mechanism implementing a possibly randomized, stationary selection policy, suggestively termed as a Random Access Model (RAM). We propose a new formulation of the FL problem which effectively captures and mitigates limited participation of data originating from infrequent, or restricted users, at the presence of a RAM. By employing the Conditional Value-at-Risk (CVaR) over the (unknown) RAM distribution, we extend the expected loss FL objective to a risk-aware objective, enabling the design of an efficient training algorithm that is completely oblivious to the RAM, and with essentially identical complexity as FedAvg. Our experiments on synthetic and benchmark datasets show that the proposed approach achieves significantly improved performance as compared with standard FL, under a variety of setups.

Repeated Random Sampling for Minimizing the Time-to-Accuracy of Learning

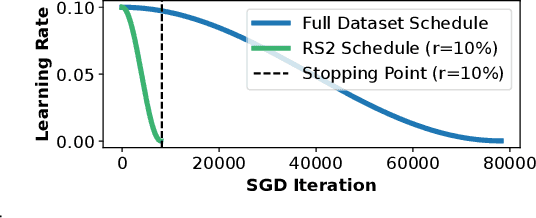
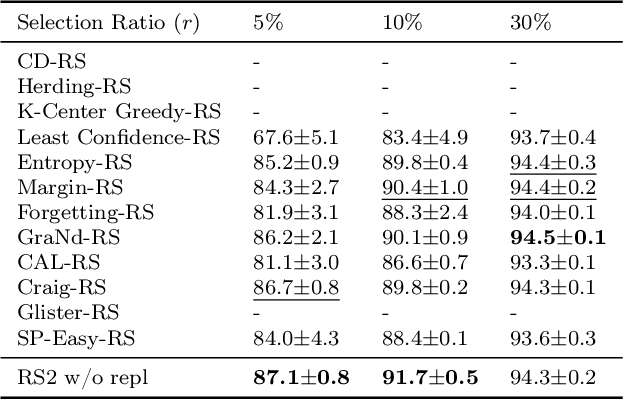
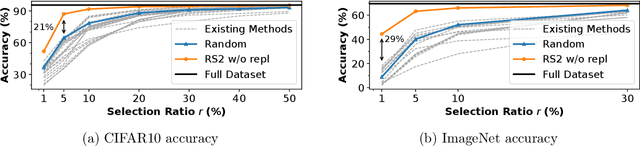
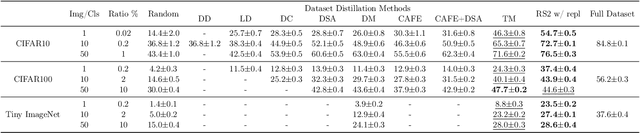
Methods for carefully selecting or generating a small set of training data to learn from, i.e., data pruning, coreset selection, and data distillation, have been shown to be effective in reducing the ever-increasing cost of training neural networks. Behind this success are rigorously designed strategies for identifying informative training examples out of large datasets. However, these strategies come with additional computational costs associated with subset selection or data distillation before training begins, and furthermore, many are shown to even under-perform random sampling in high data compression regimes. As such, many data pruning, coreset selection, or distillation methods may not reduce 'time-to-accuracy', which has become a critical efficiency measure of training deep neural networks over large datasets. In this work, we revisit a powerful yet overlooked random sampling strategy to address these challenges and introduce an approach called Repeated Sampling of Random Subsets (RSRS or RS2), where we randomly sample the subset of training data for each epoch of model training. We test RS2 against thirty state-of-the-art data pruning and data distillation methods across four datasets including ImageNet. Our results demonstrate that RS2 significantly reduces time-to-accuracy compared to existing techniques. For example, when training on ImageNet in the high-compression regime (using less than 10% of the dataset each epoch), RS2 yields accuracy improvements up to 29% compared to competing pruning methods while offering a runtime reduction of 7x. Beyond the above meta-study, we provide a convergence analysis for RS2 and discuss its generalization capability. The primary goal of our work is to establish RS2 as a competitive baseline for future data selection or distillation techniques aimed at efficient training.

Select without Fear: Almost All Mini-Batch Schedules Generalize Optimally

We establish matching upper and lower generalization error bounds for mini-batch Gradient Descent (GD) training with either deterministic or stochastic, data-independent, but otherwise arbitrary batch selection rules. We consider smooth Lipschitz-convex/nonconvex/strongly-convex loss functions, and show that classical upper bounds for Stochastic GD (SGD) also hold verbatim for such arbitrary nonadaptive batch schedules, including all deterministic ones. Further, for convex and strongly-convex losses we prove matching lower bounds directly on the generalization error uniform over the aforementioned class of batch schedules, showing that all such batch schedules generalize optimally. Lastly, for smooth (non-Lipschitz) nonconvex losses, we show that full-batch (deterministic) GD is essentially optimal, among all possible batch schedules within the considered class, including all stochastic ones.