Data-Driven Learning of Two-Stage Beamformers in Passive IRS-Assisted Systems with Inexact Oracles

We develop an efficient data-driven and model-free unsupervised learning algorithm for achieving fully passive intelligent reflective surface (IRS)-assisted optimal short/long-term beamforming in wireless communication networks. The proposed algorithm is based on a zeroth-order stochastic gradient ascent methodology, suitable for tackling two-stage stochastic nonconvex optimization problems with continuous uncertainty and unknown (or "black-box") terms present in the objective function, via the utilization of inexact evaluation oracles. We showcase that the algorithm can operate under realistic and general assumptions, and establish its convergence rate close to some stationary point of the associated two-stage (i.e., short/long-term) problem, particularly in cases where the second-stage (i.e., short-term) beamforming problem (e.g., transmit precoding) is solved inexactly using an arbitrary (inexact) oracle. The proposed algorithm is applicable on a wide variety of IRS-assisted optimal beamforming settings, while also being able to operate without (cascaded) channel model assumptions or knowledge of channel statistics, and over arbitrary IRS physical configurations; thus, no active sensing capability at the IRS(s) is needed. Our algorithm is numerically demonstrated to be very effective in a range of experiments pertaining to a well-studied MISO downlink model, including scenarios demanding physical IRS tuning (e.g., directly through varactor capacitances), even in large-scale regimes.

Strong Duality Relations in Nonconvex Risk-Constrained Learning

We establish strong duality relations for functional two-step compositional risk-constrained learning problems with multiple nonconvex loss functions and/or learning constraints, regardless of nonconvexity and under a minimal set of technical assumptions. Our results in particular imply zero duality gaps within the class of problems under study, both extending and improving on the state of the art in (risk-neutral) constrained learning. More specifically, we consider risk objectives/constraints which involve real-valued convex and positively homogeneous risk measures admitting dual representations with bounded risk envelopes, generalizing expectations and including popular examples, such as the conditional value-at-risk (CVaR), the mean-absolute deviation (MAD), and more generally all real-valued coherent risk measures on integrable losses as special cases. Our results are based on recent advances in risk-constrained nonconvex programming in infinite dimensions, which rely on a remarkable new application of J. J. Uhl's convexity theorem, which is an extension of A. A. Lyapunov's convexity theorem for general, infinite dimensional Banach spaces. By specializing to the risk-neutral setting, we demonstrate, for the first time, that constrained classification and regression can be treated under a unifying lens, while dispensing certain restrictive assumptions enforced in the current literature, yielding a new state-of-the-art strong duality framework for nonconvex constrained learning.

Efficient KLMS and KRLS Algorithms: A Random Fourier Feature Perspective

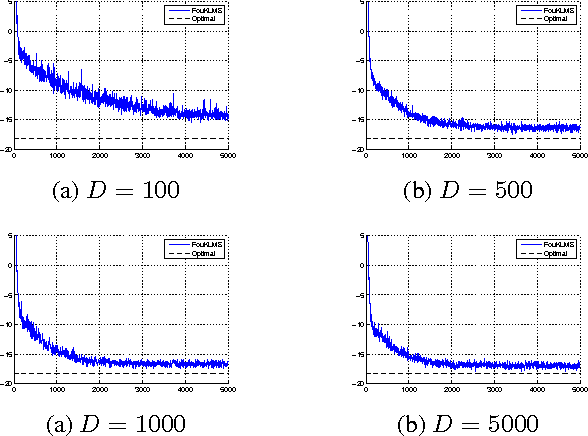
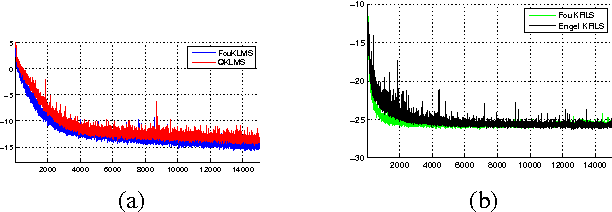
We present a new framework for online Least Squares algorithms for nonlinear modeling in RKH spaces (RKHS). Instead of implicitly mapping the data to a RKHS (e.g., kernel trick), we map the data to a finite dimensional Euclidean space, using random features of the kernel's Fourier transform. The advantage is that, the inner product of the mapped data approximates the kernel function. The resulting "linear" algorithm does not require any form of sparsification, since, in contrast to all existing algorithms, the solution's size remains fixed and does not increase with the iteration steps. As a result, the obtained algorithms are computationally significantly more efficient compared to previously derived variants, while, at the same time, they converge at similar speeds and to similar error floors.