STANLEY: Stochastic Gradient Anisotropic Langevin Dynamics for Learning Energy-Based Models

We propose in this paper, STANLEY, a STochastic gradient ANisotropic LangEvin dYnamics, for sampling high dimensional data. With the growing efficacy and potential of Energy-Based modeling, also known as non-normalized probabilistic modeling, for modeling a generative process of different natures of high dimensional data observations, we present an end-to-end learning algorithm for Energy-Based models (EBM) with the purpose of improving the quality of the resulting sampled data points. While the unknown normalizing constant of EBMs makes the training procedure intractable, resorting to Markov Chain Monte Carlo (MCMC) is in general a viable option. Realizing what MCMC entails for the EBM training, we propose in this paper, a novel high dimensional sampling method, based on an anisotropic stepsize and a gradient-informed covariance matrix, embedded into a discretized Langevin diffusion. We motivate the necessity for an anisotropic update of the negative samples in the Markov Chain by the nonlinearity of the backbone of the EBM, here a Convolutional Neural Network. Our resulting method, namely STANLEY, is an optimization algorithm for training Energy-Based models via our newly introduced MCMC method. We provide a theoretical understanding of our sampling scheme by proving that the sampler leads to a geometrically uniformly ergodic Markov Chain. Several image generation experiments are provided in our paper to show the effectiveness of our method.

Variational Flow Graphical Model

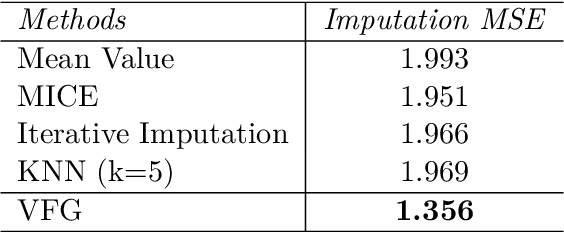
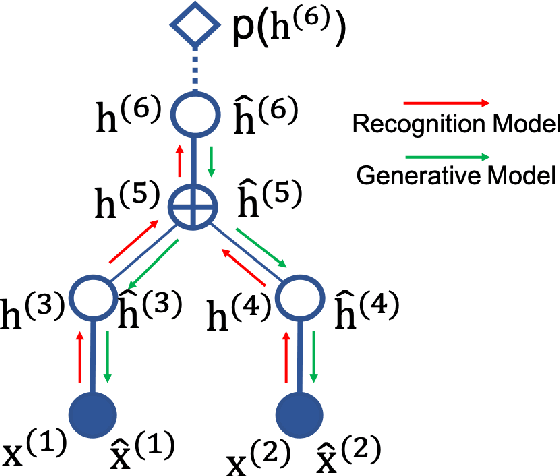
This paper introduces a novel approach to embed flow-based models with hierarchical structures. The proposed framework is named Variational Flow Graphical (VFG) Model. VFGs learn the representation of high dimensional data via a message-passing scheme by integrating flow-based functions through variational inference. By leveraging the expressive power of neural networks, VFGs produce a representation of the data using a lower dimension, thus overcoming the drawbacks of many flow-based models, usually requiring a high dimensional latent space involving many trivial variables. Aggregation nodes are introduced in the VFG models to integrate forward-backward hierarchical information via a message passing scheme. Maximizing the evidence lower bound (ELBO) of data likelihood aligns the forward and backward messages in each aggregation node achieving a consistency node state. Algorithms have been developed to learn model parameters through gradient updating regarding the ELBO objective. The consistency of aggregation nodes enable VFGs to be applicable in tractable inference on graphical structures. Besides representation learning and numerical inference, VFGs provide a new approach for distribution modeling on datasets with graphical latent structures. Additionally, theoretical study shows that VFGs are universal approximators by leveraging the implicitly invertible flow-based structures. With flexible graphical structures and superior excessive power, VFGs could potentially be used to improve probabilistic inference. In the experiments, VFGs achieves improved evidence lower bound (ELBO) and likelihood values on multiple datasets.

On Distributed Adaptive Optimization with Gradient Compression

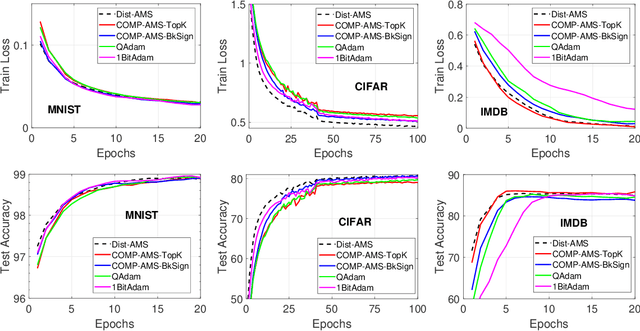
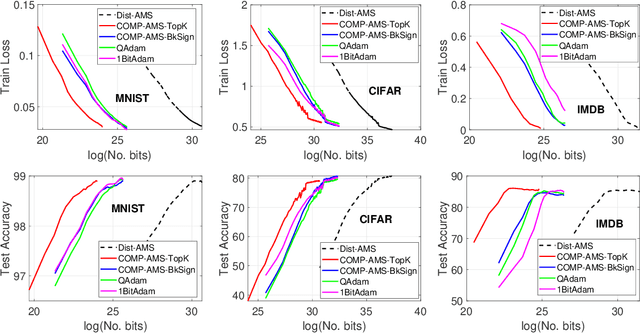
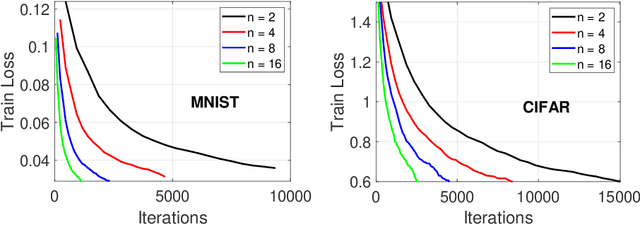
We study COMP-AMS, a distributed optimization framework based on gradient averaging and adaptive AMSGrad algorithm. Gradient compression with error feedback is applied to reduce the communication cost in the gradient transmission process. Our convergence analysis of COMP-AMS shows that such compressed gradient averaging strategy yields same convergence rate as standard AMSGrad, and also exhibits the linear speedup effect w.r.t. the number of local workers. Compared with recently proposed protocols on distributed adaptive methods, COMP-AMS is simple and convenient. Numerical experiments are conducted to justify the theoretical findings, and demonstrate that the proposed method can achieve same test accuracy as the full-gradient AMSGrad with substantial communication savings. With its simplicity and efficiency, COMP-AMS can serve as a useful distributed training framework for adaptive gradient methods.

Joint learning of object graph and relation graph for visual question answering

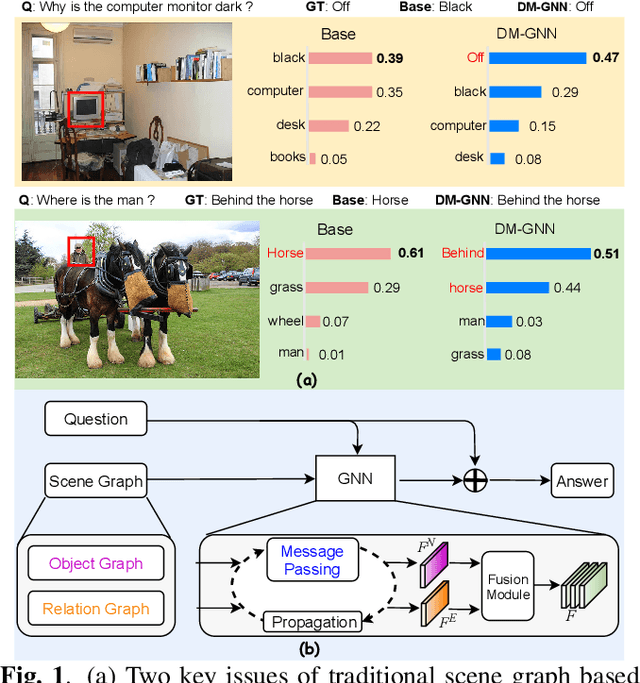
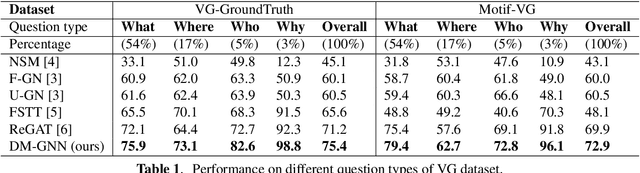
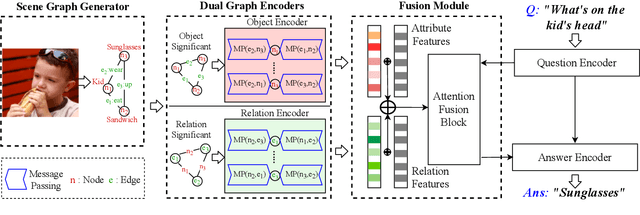
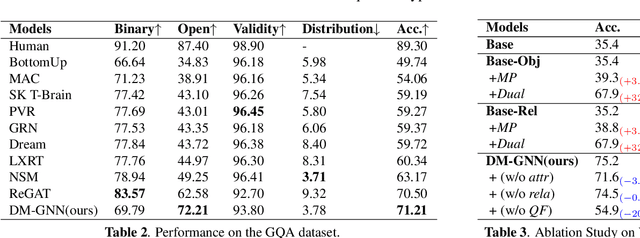
Modeling visual question answering(VQA) through scene graphs can significantly improve the reasoning accuracy and interpretability. However, existing models answer poorly for complex reasoning questions with attributes or relations, which causes false attribute selection or missing relation in Figure 1(a). It is because these models cannot balance all kinds of information in scene graphs, neglecting relation and attribute information. In this paper, we introduce a novel Dual Message-passing enhanced Graph Neural Network (DM-GNN), which can obtain a balanced representation by properly encoding multi-scale scene graph information. Specifically, we (i)transform the scene graph into two graphs with diversified focuses on objects and relations; Then we design a dual structure to encode them, which increases the weights from relations (ii)fuse the encoder output with attribute features, which increases the weights from attributes; (iii)propose a message-passing mechanism to enhance the information transfer between objects, relations and attributes. We conduct extensive experiments on datasets including GQA, VG, motif-VG and achieve new state of the art.

A Class of Two-Timescale Stochastic EM Algorithms for Nonconvex Latent Variable Models

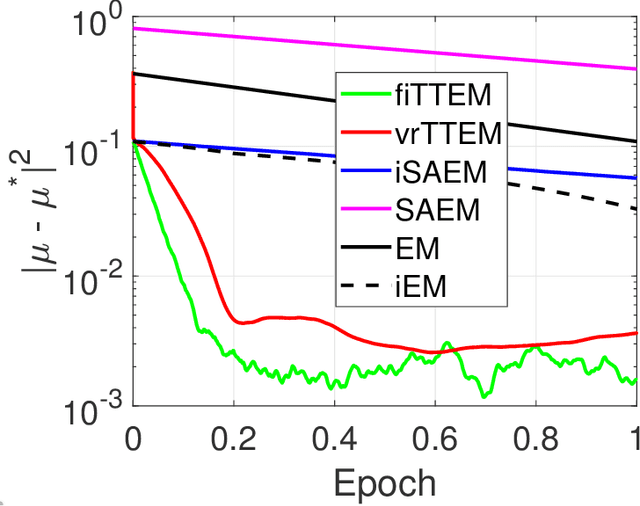
The Expectation-Maximization (EM) algorithm is a popular choice for learning latent variable models. Variants of the EM have been initially introduced, using incremental updates to scale to large datasets, and using Monte Carlo (MC) approximations to bypass the intractable conditional expectation of the latent data for most nonconvex models. In this paper, we propose a general class of methods called Two-Timescale EM Methods based on a two-stage approach of stochastic updates to tackle an essential nonconvex optimization task for latent variable models. We motivate the choice of a double dynamic by invoking the variance reduction virtue of each stage of the method on both sources of noise: the index sampling for the incremental update and the MC approximation. We establish finite-time and global convergence bounds for nonconvex objective functions. Numerical applications on various models such as deformable template for image analysis or nonlinear models for pharmacokinetics are also presented to illustrate our findings.

Fed-LAMB: Layerwise and Dimensionwise Locally Adaptive Optimization Algorithm

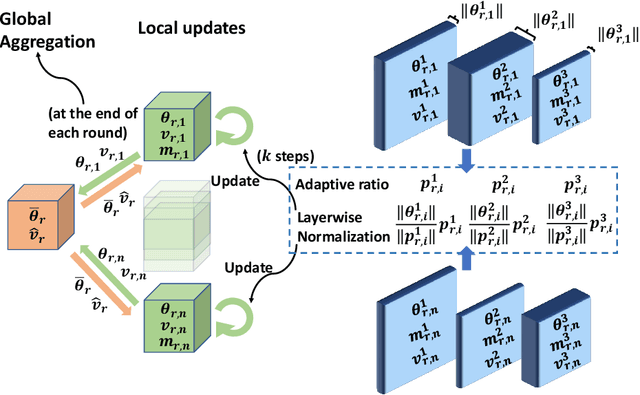
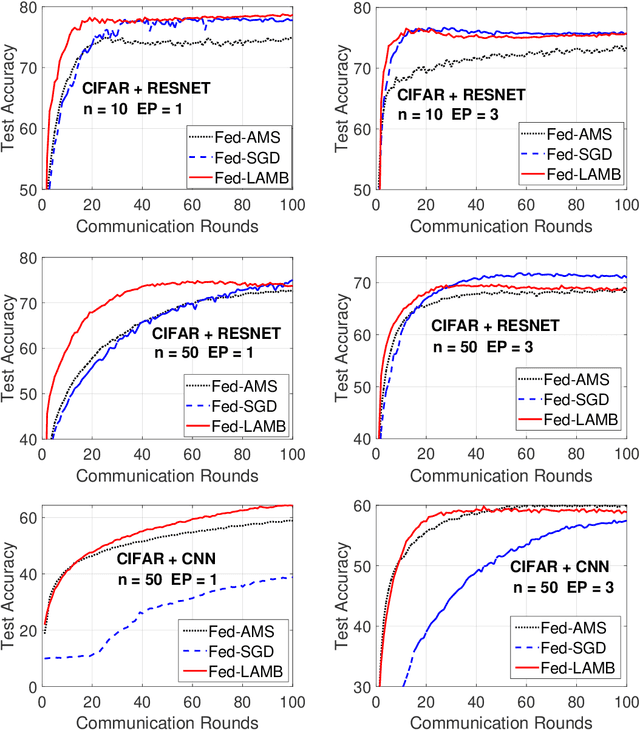
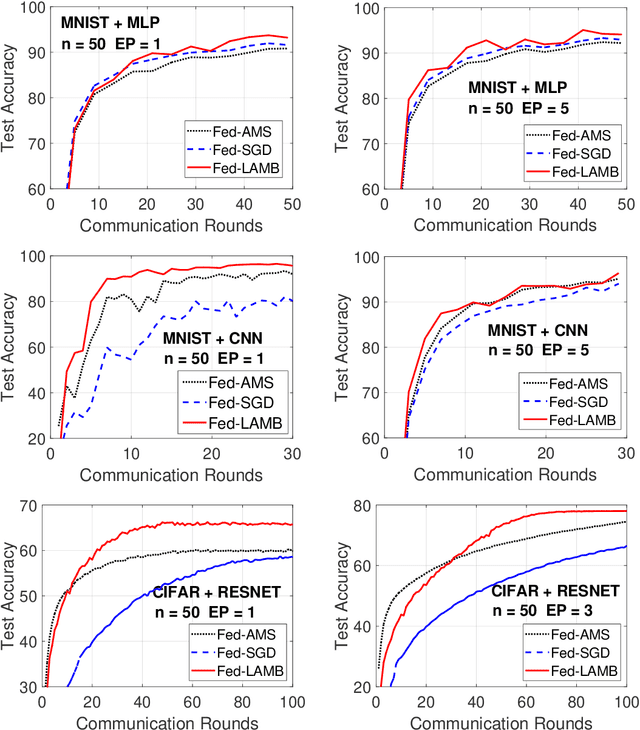
In the emerging paradigm of federated learning (FL), large amount of clients, such as mobile devices, are used to train possibly high-dimensional models on their respective data. Due to the low bandwidth of mobile devices, decentralized optimization methods need to shift the computation burden from those clients to the computation server while preserving privacy and reasonable communication cost. In this paper, we focus on the training of deep, as in multilayered, neural networks, under the FL settings. We present Fed-LAMB, a novel federated learning method based on a layerwise and dimensionwise updates of the local models, alleviating the nonconvexity and the multilayered nature of the optimization task at hand. We provide a thorough finite-time convergence analysis for Fed-LAMB characterizing how fast its gradient decreases. We provide experimental results under iid and non-iid settings to corroborate not only our theory, but also exhibit the faster convergence of our method, compared to the state-of-the-art.

On the Convergence of Decentralized Adaptive Gradient Methods

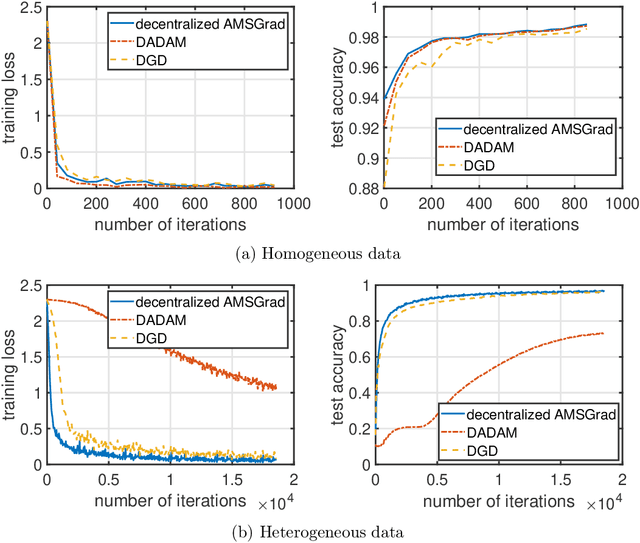
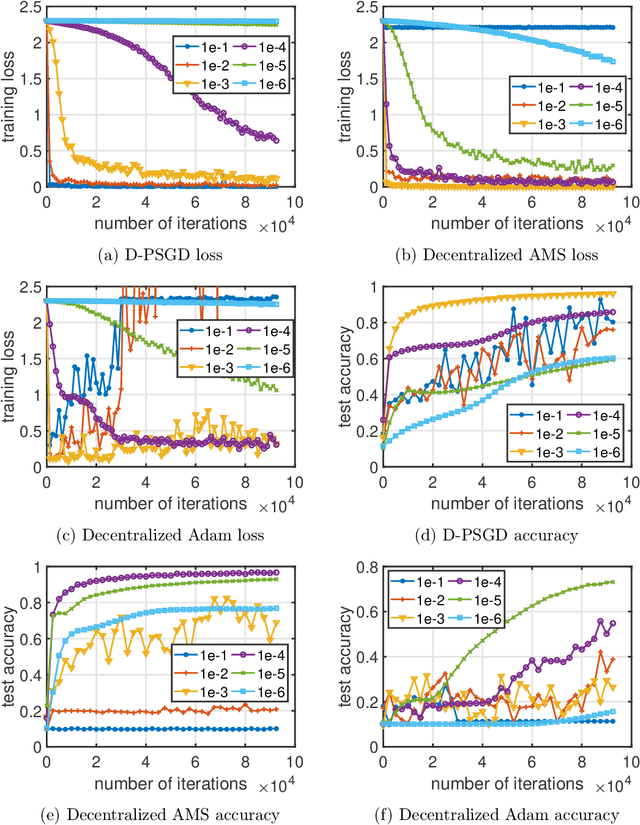
Adaptive gradient methods including Adam, AdaGrad, and their variants have been very successful for training deep learning models, such as neural networks. Meanwhile, given the need for distributed computing, distributed optimization algorithms are rapidly becoming a focal point. With the growth of computing power and the need for using machine learning models on mobile devices, the communication cost of distributed training algorithms needs careful consideration. In this paper, we introduce novel convergent decentralized adaptive gradient methods and rigorously incorporate adaptive gradient methods into decentralized training procedures. Specifically, we propose a general algorithmic framework that can convert existing adaptive gradient methods to their decentralized counterparts. In addition, we thoroughly analyze the convergence behavior of the proposed algorithmic framework and show that if a given adaptive gradient method converges, under some specific conditions, then its decentralized counterpart is also convergent. We illustrate the benefit of our generic decentralized framework on a prototype method, i.e., AMSGrad, both theoretically and numerically.

FedSKETCH: Communication-Efficient and Private Federated Learning via Sketching

Communication complexity and privacy are the two key challenges in Federated Learning where the goal is to perform a distributed learning through a large volume of devices. In this work, we introduce FedSKETCH and FedSKETCHGATE algorithms to address both challenges in Federated learning jointly, where these algorithms are intended to be used for homogeneous and heterogeneous data distribution settings respectively. The key idea is to compress the accumulation of local gradients using count sketch, therefore, the server does not have access to the gradients themselves which provides privacy. Furthermore, due to the lower dimension of sketching used, our method exhibits communication-efficiency property as well. We provide, for the aforementioned schemes, sharp convergence guarantees. Finally, we back up our theory with various set of experiments.

On the Global Convergence of (Fast) Incremental Expectation Maximization Methods

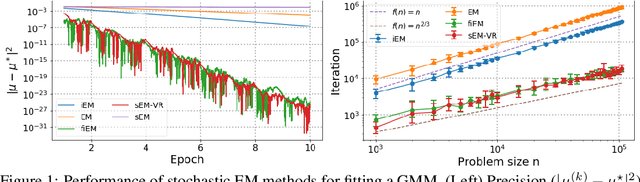
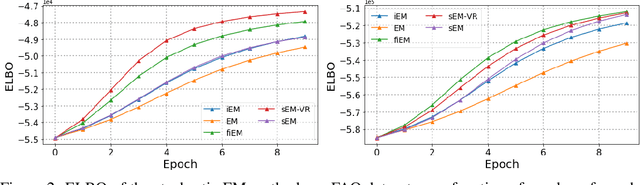
The EM algorithm is one of the most popular algorithm for inference in latent data models. The original formulation of the EM algorithm does not scale to large data set, because the whole data set is required at each iteration of the algorithm. To alleviate this problem, Neal and Hinton have proposed an incremental version of the EM (iEM) in which at each iteration the conditional expectation of the latent data (E-step) is updated only for a mini-batch of observations. Another approach has been proposed by Capp\'e and Moulines in which the E-step is replaced by a stochastic approximation step, closely related to stochastic gradient. In this paper, we analyze incremental and stochastic version of the EM algorithm as well as the variance reduced-version of Chen et. al. in a common unifying framework. We also introduce a new version incremental version, inspired by the SAGA algorithm by Defazio et. al. We establish non-asymptotic convergence bounds for global convergence. Numerical applications are presented in this article to illustrate our findings.

Non-asymptotic Analysis of Biased Stochastic Approximation Scheme

Stochastic approximation (SA) is a key method used in statistical learning. Recently, its non-asymptotic convergence analysis has been considered in many papers. However, most of the prior analyses are made under restrictive assumptions such as unbiased gradient estimates and convex objective function, which significantly limit their applications to sophisticated tasks such as online and reinforcement learning. These restrictions are all essentially relaxed in this work. In particular, we analyze a general SA scheme to minimize a non-convex, smooth objective function. We consider update procedure whose drift term depends on a state-dependent Markov chain and the mean field is not necessarily of gradient type, covering approximate second-order method and allowing asymptotic bias for the one-step updates. We illustrate these settings with the online EM algorithm and the policy-gradient method for average reward maximization in reinforcement learning.