Learning Flexible Time-windowed Granger Causality Integrating Heterogeneous Interventional Time Series Data

Granger causality, commonly used for inferring causal structures from time series data, has been adopted in widespread applications across various fields due to its intuitive explainability and high compatibility with emerging deep neural network prediction models. To alleviate challenges in better deciphering causal structures unambiguously from time series, the use of interventional data has become a practical approach. However, existing methods have yet to be explored in the context of imperfect interventions with unknown targets, which are more common and often more beneficial in a wide range of real-world applications. Additionally, the identifiability issues of Granger causality with unknown interventional targets in complex network models remain unsolved. Our work presents a theoretically-grounded method that infers Granger causal structure and identifies unknown targets by leveraging heterogeneous interventional time series data. We further illustrate that learning Granger causal structure and recovering interventional targets can mutually promote each other. Comparative experiments demonstrate that our method outperforms several robust baseline methods in learning Granger causal structure from interventional time series data.

Towards Invariant Time Series Forecasting in Smart Cities

In the transformative landscape of smart cities, the integration of the cutting-edge web technologies into time series forecasting presents a pivotal opportunity to enhance urban planning, sustainability, and economic growth. The advancement of deep neural networks has significantly improved forecasting performance. However, a notable challenge lies in the ability of these models to generalize well to out-of-distribution (OOD) time series data. The inherent spatial heterogeneity and domain shifts across urban environments create hurdles that prevent models from adapting and performing effectively in new urban environments. To tackle this problem, we propose a solution to derive invariant representations for more robust predictions under different urban environments instead of relying on spurious correlation across urban environments for better generalizability. Through extensive experiments on both synthetic and real-world data, we demonstrate that our proposed method outperforms traditional time series forecasting models when tackling domain shifts in changing urban environments. The effectiveness and robustness of our method can be extended to diverse fields including climate modeling, urban planning, and smart city resource management.

Dynamic Incremental Optimization for Best Subset Selection

Best subset selection is considered the `gold standard' for many sparse learning problems. A variety of optimization techniques have been proposed to attack this non-smooth non-convex problem. In this paper, we investigate the dual forms of a family of $\ell_0$-regularized problems. An efficient primal-dual algorithm is developed based on the primal and dual problem structures. By leveraging the dual range estimation along with the incremental strategy, our algorithm potentially reduces redundant computation and improves the solutions of best subset selection. Theoretical analysis and experiments on synthetic and real-world datasets validate the efficiency and statistical properties of the proposed solutions.

Causal Bayesian Optimization via Exogenous Distribution Learning

Maximizing a target variable as an operational objective in a structured causal model is an important problem. Existing Causal Bayesian Optimization (CBO) methods either rely on hard interventions that alter the causal structure to maximize the reward; or introduce action nodes to endogenous variables so that the data generation mechanisms are adjusted to achieve the objective. In this paper, a novel method is introduced to learn the distribution of exogenous variables, which is typically ignored or marginalized through expectation by existing methods. Exogenous distribution learning improves the approximation accuracy of structured causal models in a surrogate model that is usually trained with limited observational data. Moreover, the learned exogenous distribution extends existing CBO to general causal schemes beyond Additive Noise Models (ANM). The recovery of exogenous variables allows us to use a more flexible prior for noise or unobserved hidden variables. A new CBO method is developed by leveraging the learned exogenous distribution. Experiments on different datasets and applications show the benefits of our proposed method.

Word Embedding with Neural Probabilistic Prior

To improve word representation learning, we propose a probabilistic prior which can be seamlessly integrated with word embedding models. Different from previous methods, word embedding is taken as a probabilistic generative model, and it enables us to impose a prior regularizing word representation learning. The proposed prior not only enhances the representation of embedding vectors but also improves the model's robustness and stability. The structure of the proposed prior is simple and effective, and it can be easily implemented and flexibly plugged in most existing word embedding models. Extensive experiments show the proposed method improves word representation on various tasks.

Variational Flow Graphical Model

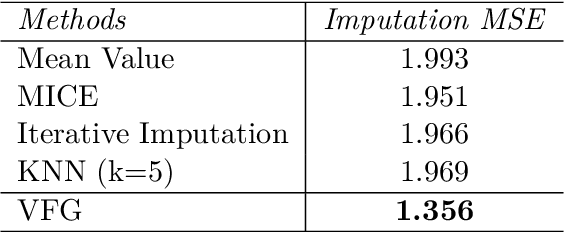
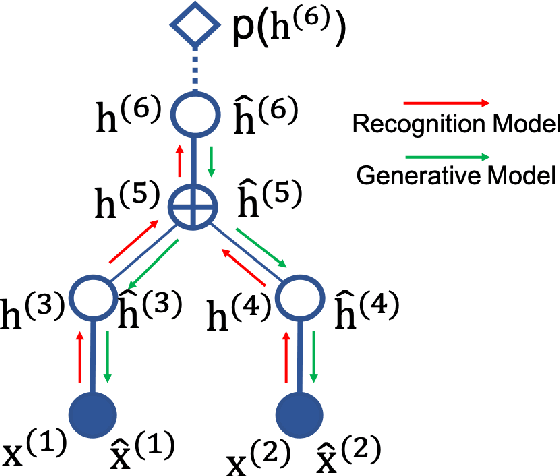
This paper introduces a novel approach to embed flow-based models with hierarchical structures. The proposed framework is named Variational Flow Graphical (VFG) Model. VFGs learn the representation of high dimensional data via a message-passing scheme by integrating flow-based functions through variational inference. By leveraging the expressive power of neural networks, VFGs produce a representation of the data using a lower dimension, thus overcoming the drawbacks of many flow-based models, usually requiring a high dimensional latent space involving many trivial variables. Aggregation nodes are introduced in the VFG models to integrate forward-backward hierarchical information via a message passing scheme. Maximizing the evidence lower bound (ELBO) of data likelihood aligns the forward and backward messages in each aggregation node achieving a consistency node state. Algorithms have been developed to learn model parameters through gradient updating regarding the ELBO objective. The consistency of aggregation nodes enable VFGs to be applicable in tractable inference on graphical structures. Besides representation learning and numerical inference, VFGs provide a new approach for distribution modeling on datasets with graphical latent structures. Additionally, theoretical study shows that VFGs are universal approximators by leveraging the implicitly invertible flow-based structures. With flexible graphical structures and superior excessive power, VFGs could potentially be used to improve probabilistic inference. In the experiments, VFGs achieves improved evidence lower bound (ELBO) and likelihood values on multiple datasets.

Best Subset Selection with Efficient Primal-Dual Algorithm

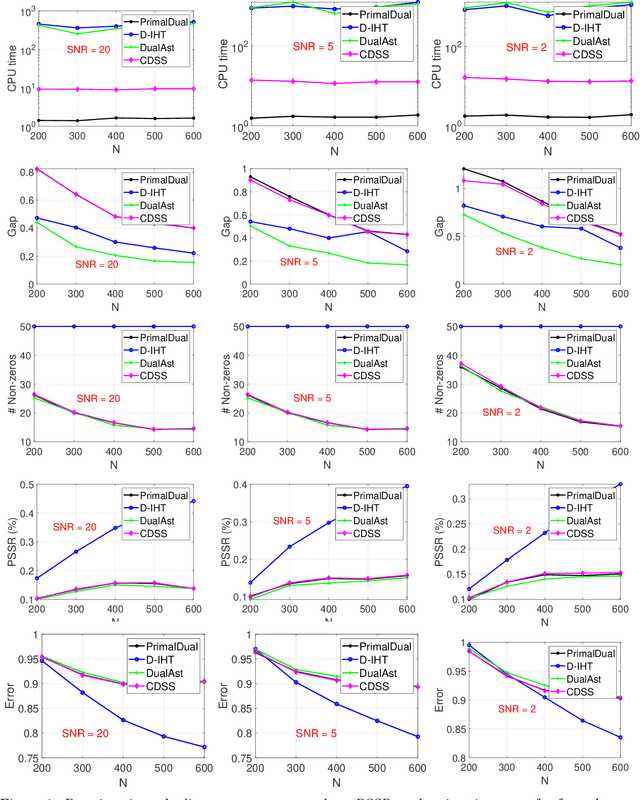
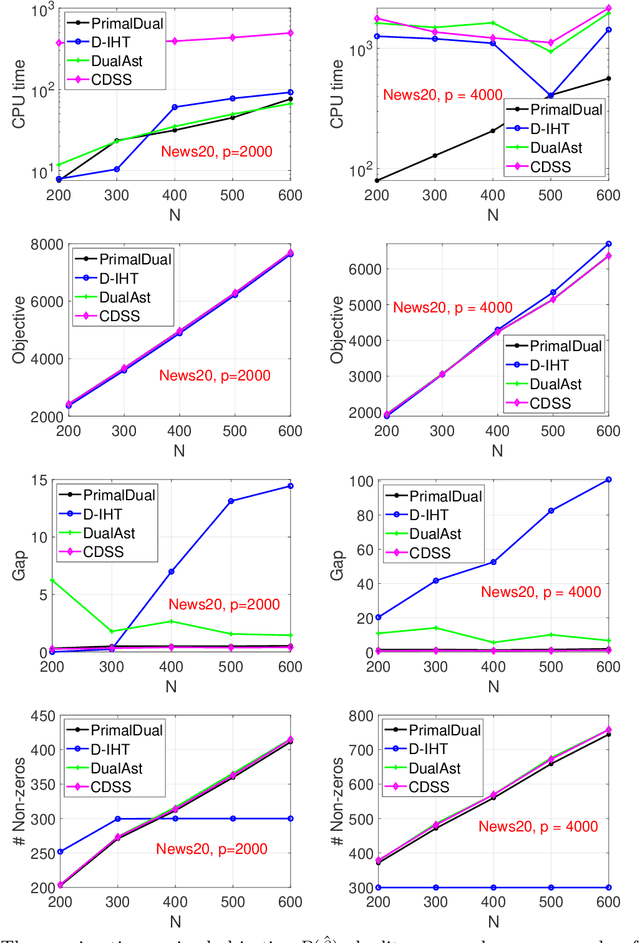
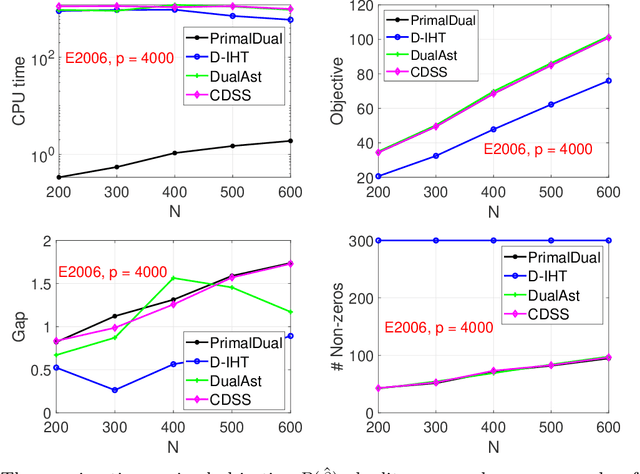
Best subset selection is considered the `gold standard' for many sparse learning problems. A variety of optimization techniques have been proposed to attack this non-convex and NP-hard problem. In this paper, we investigate the dual forms of a family of $\ell_0$-regularized problems. An efficient primal-dual method has been developed based on the primal and dual problem structures. By leveraging the dual range estimation along with the incremental strategy, our algorithm potentially reduces redundant computation and improves the solutions of best subset selection. Theoretical analysis and experiments on synthetic and real-world datasets validate the efficiency and statistical properties of the proposed solutions.

Safe Active Feature Selection for Sparse Learning

We present safe active incremental feature selection~(SAIF) to scale up the computation of LASSO solutions. SAIF does not require a solution from a heavier penalty parameter as in sequential screening or updating the full model for each iteration as in dynamic screening. Different from these existing screening methods, SAIF starts from a small number of features and incrementally recruits active features and updates the significantly reduced model. Hence, it is much more computationally efficient and scalable with the number of features. More critically, SAIF has the safe guarantee as it has the convergence guarantee to the optimal solution to the original full LASSO problem. Such an incremental procedure and theoretical convergence guarantee can be extended to fused LASSO problems. Compared with state-of-the-art screening methods as well as working set and homotopy methods, which may not always guarantee the optimal solution, SAIF can achieve superior or comparable efficiency and high scalability with the safe guarantee when facing extremely high dimensional data sets. Experiments with both synthetic and real-world data sets show that SAIF can be up to 50 times faster than dynamic screening, and hundreds of times faster than computing LASSO or fused LASSO solutions without screening.