Variational Flow Graphical Model
Paper and Code
Jul 06, 2022
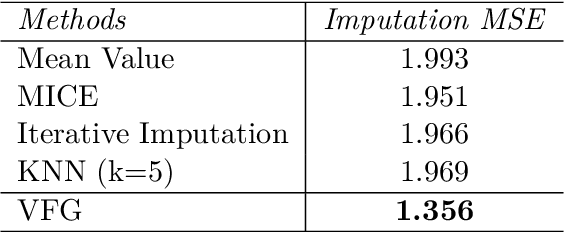
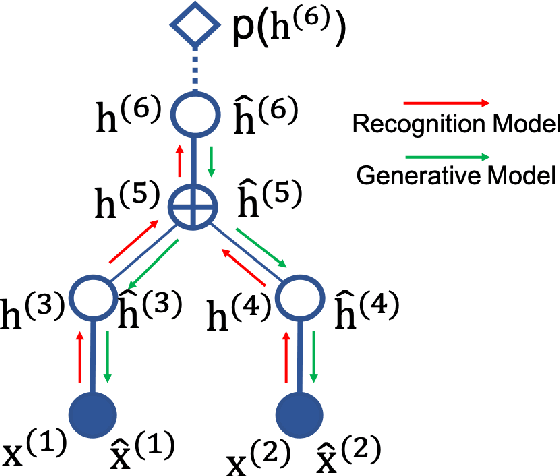

This paper introduces a novel approach to embed flow-based models with hierarchical structures. The proposed framework is named Variational Flow Graphical (VFG) Model. VFGs learn the representation of high dimensional data via a message-passing scheme by integrating flow-based functions through variational inference. By leveraging the expressive power of neural networks, VFGs produce a representation of the data using a lower dimension, thus overcoming the drawbacks of many flow-based models, usually requiring a high dimensional latent space involving many trivial variables. Aggregation nodes are introduced in the VFG models to integrate forward-backward hierarchical information via a message passing scheme. Maximizing the evidence lower bound (ELBO) of data likelihood aligns the forward and backward messages in each aggregation node achieving a consistency node state. Algorithms have been developed to learn model parameters through gradient updating regarding the ELBO objective. The consistency of aggregation nodes enable VFGs to be applicable in tractable inference on graphical structures. Besides representation learning and numerical inference, VFGs provide a new approach for distribution modeling on datasets with graphical latent structures. Additionally, theoretical study shows that VFGs are universal approximators by leveraging the implicitly invertible flow-based structures. With flexible graphical structures and superior excessive power, VFGs could potentially be used to improve probabilistic inference. In the experiments, VFGs achieves improved evidence lower bound (ELBO) and likelihood values on multiple datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge