Learning Flexible Time-windowed Granger Causality Integrating Heterogeneous Interventional Time Series Data

Granger causality, commonly used for inferring causal structures from time series data, has been adopted in widespread applications across various fields due to its intuitive explainability and high compatibility with emerging deep neural network prediction models. To alleviate challenges in better deciphering causal structures unambiguously from time series, the use of interventional data has become a practical approach. However, existing methods have yet to be explored in the context of imperfect interventions with unknown targets, which are more common and often more beneficial in a wide range of real-world applications. Additionally, the identifiability issues of Granger causality with unknown interventional targets in complex network models remain unsolved. Our work presents a theoretically-grounded method that infers Granger causal structure and identifies unknown targets by leveraging heterogeneous interventional time series data. We further illustrate that learning Granger causal structure and recovering interventional targets can mutually promote each other. Comparative experiments demonstrate that our method outperforms several robust baseline methods in learning Granger causal structure from interventional time series data.

Towards Invariant Time Series Forecasting in Smart Cities

In the transformative landscape of smart cities, the integration of the cutting-edge web technologies into time series forecasting presents a pivotal opportunity to enhance urban planning, sustainability, and economic growth. The advancement of deep neural networks has significantly improved forecasting performance. However, a notable challenge lies in the ability of these models to generalize well to out-of-distribution (OOD) time series data. The inherent spatial heterogeneity and domain shifts across urban environments create hurdles that prevent models from adapting and performing effectively in new urban environments. To tackle this problem, we propose a solution to derive invariant representations for more robust predictions under different urban environments instead of relying on spurious correlation across urban environments for better generalizability. Through extensive experiments on both synthetic and real-world data, we demonstrate that our proposed method outperforms traditional time series forecasting models when tackling domain shifts in changing urban environments. The effectiveness and robustness of our method can be extended to diverse fields including climate modeling, urban planning, and smart city resource management.

Spectral Convolutional Conditional Neural Processes

Conditional Neural Processes (CNPs) constitute a family of probabilistic models that harness the flexibility of neural networks to parameterize stochastic processes. Their capability to furnish well-calibrated predictions, combined with simple maximum-likelihood training, has established them as appealing solutions for addressing various learning problems, with a particular emphasis on meta-learning. A prominent member of this family, Convolutional Conditional Neural Processes (ConvCNPs), utilizes convolution to explicitly introduce translation equivariance as an inductive bias. However, ConvCNP's reliance on local discrete kernels in its convolution layers can pose challenges in capturing long-range dependencies and complex patterns within the data, especially when dealing with limited and irregularly sampled observations from a new task. Building on the successes of Fourier neural operators (FNOs) for approximating the solution operators of parametric partial differential equations (PDEs), we propose Spectral Convolutional Conditional Neural Processes (SConvCNPs), a new addition to the NPs family that allows for more efficient representation of functions in the frequency domain.

Adaptive Conditional Quantile Neural Processes

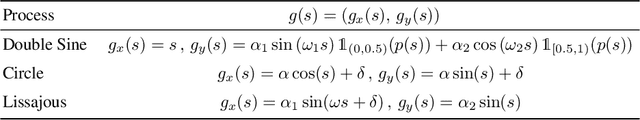
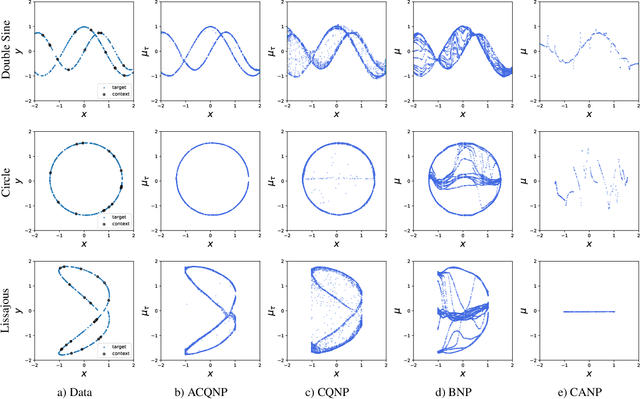
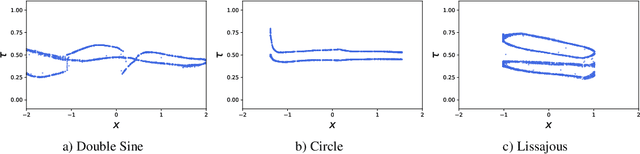
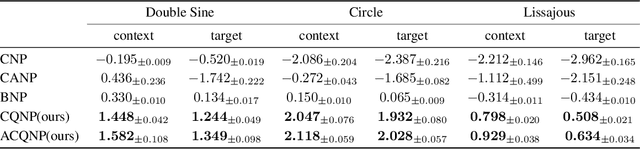
Neural processes are a family of probabilistic models that inherit the flexibility of neural networks to parameterize stochastic processes. Despite providing well-calibrated predictions, especially in regression problems, and quick adaptation to new tasks, the Gaussian assumption that is commonly used to represent the predictive likelihood fails to capture more complicated distributions such as multimodal ones. To overcome this limitation, we propose Conditional Quantile Neural Processes (CQNPs), a new member of the neural processes family, which exploits the attractive properties of quantile regression in modeling the distributions irrespective of their form. By introducing an extension of quantile regression where the model learns to focus on estimating informative quantiles, we show that the sampling efficiency and prediction accuracy can be further enhanced. Our experiments with real and synthetic datasets demonstrate substantial improvements in predictive performance compared to the baselines, and better modeling of heterogeneous distributions' characteristics such as multimodality.

MoReL: Multi-omics Relational Learning

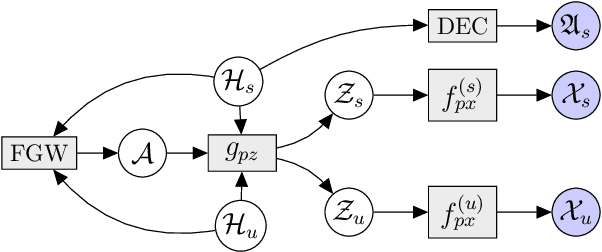
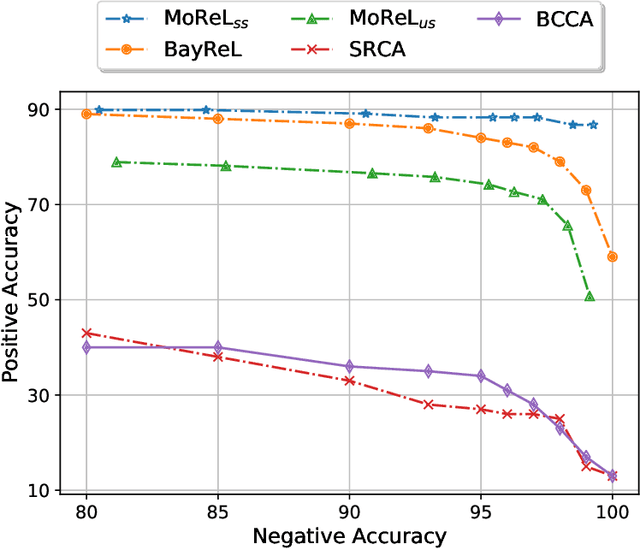
Multi-omics data analysis has the potential to discover hidden molecular interactions, revealing potential regulatory and/or signal transduction pathways for cellular processes of interest when studying life and disease systems. One of critical challenges when dealing with real-world multi-omics data is that they may manifest heterogeneous structures and data quality as often existing data may be collected from different subjects under different conditions for each type of omics data. We propose a novel deep Bayesian generative model to efficiently infer a multi-partite graph encoding molecular interactions across such heterogeneous views, using a fused Gromov-Wasserstein (FGW) regularization between latent representations of corresponding views for integrative analysis. With such an optimal transport regularization in the deep Bayesian generative model, it not only allows incorporating view-specific side information, either with graph-structured or unstructured data in different views, but also increases the model flexibility with the distribution-based regularization. This allows efficient alignment of heterogeneous latent variable distributions to derive reliable interaction predictions compared to the existing point-based graph embedding methods. Our experiments on several real-world datasets demonstrate enhanced performance of MoReL in inferring meaningful interactions compared to existing baselines.

Bayesian Graph Contrastive Learning

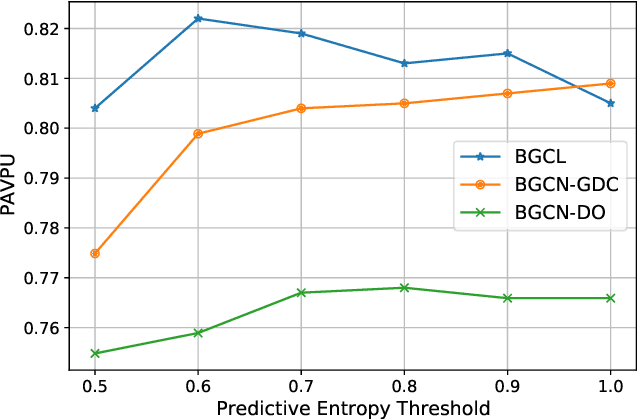
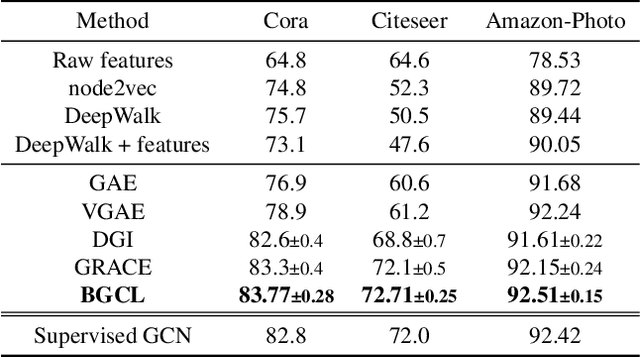
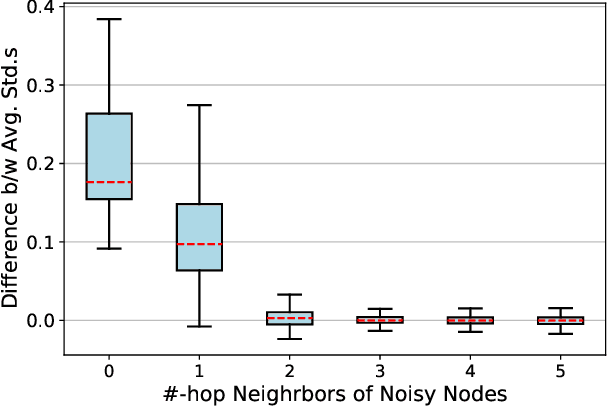
Contrastive learning has become a key component of self-supervised learning approaches for graph-structured data. However, despite their success, existing graph contrastive learning methods are incapable of uncertainty quantification for node representations or their downstream tasks, limiting their application in high-stakes domains. In this paper, we propose a novel Bayesian perspective of graph contrastive learning methods showing random augmentations leads to stochastic encoders. As a result, our proposed method represents each node by a distribution in the latent space in contrast to existing techniques which embed each node to a deterministic vector. By learning distributional representations, we provide uncertainty estimates in downstream graph analytics tasks and increase the expressive power of the predictive model. In addition, we propose a Bayesian framework to infer the probability of perturbations in each view of the contrastive model, eliminating the need for a computationally expensive search for hyperparameter tuning. We empirically show a considerable improvement in performance compared to existing state-of-the-art methods on several benchmark datasets.

BayReL: Bayesian Relational Learning for Multi-omics Data Integration

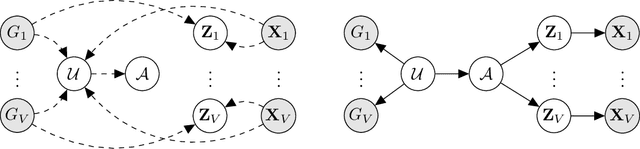
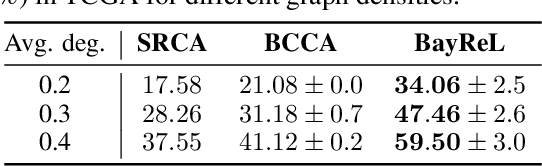
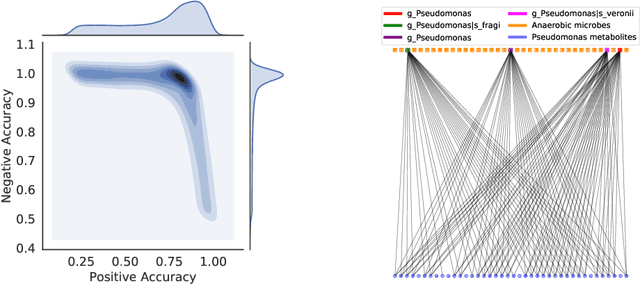
High-throughput molecular profiling technologies have produced high-dimensional multi-omics data, enabling systematic understanding of living systems at the genome scale. Studying molecular interactions across different data types helps reveal signal transduction mechanisms across different classes of molecules. In this paper, we develop a novel Bayesian representation learning method that infers the relational interactions across multi-omics data types. Our method, Bayesian Relational Learning (BayReL) for multi-omics data integration, takes advantage of a priori known relationships among the same class of molecules, modeled as a graph at each corresponding view, to learn view-specific latent variables as well as a multi-partite graph that encodes the interactions across views. Our experiments on several real-world datasets demonstrate enhanced performance of BayReL in inferring meaningful interactions compared to existing baselines.

Bayesian Graph Neural Networks with Adaptive Connection Sampling

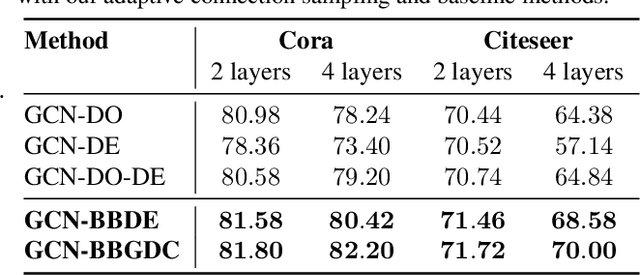
We propose a unified framework for adaptive connection sampling in graph neural networks (GNNs) that generalizes existing stochastic regularization methods for training GNNs. The proposed framework not only alleviates over-smoothing and over-fitting tendencies of deep GNNs, but also enables learning with uncertainty in graph analytic tasks with GNNs. Instead of using fixed sampling rates or hand-tuning them as model hyperparameters in existing stochastic regularization methods, our adaptive connection sampling can be trained jointly with GNN model parameters in both global and local fashions. GNN training with adaptive connection sampling is shown to be mathematically equivalent to an efficient approximation of training Bayesian GNNs. Experimental results with ablation studies on benchmark datasets validate that adaptively learning the sampling rate given graph training data is the key to boost the performance of GNNs in semi-supervised node classification, less prone to over-smoothing and over-fitting with more robust prediction.

Semi-Implicit Stochastic Recurrent Neural Networks

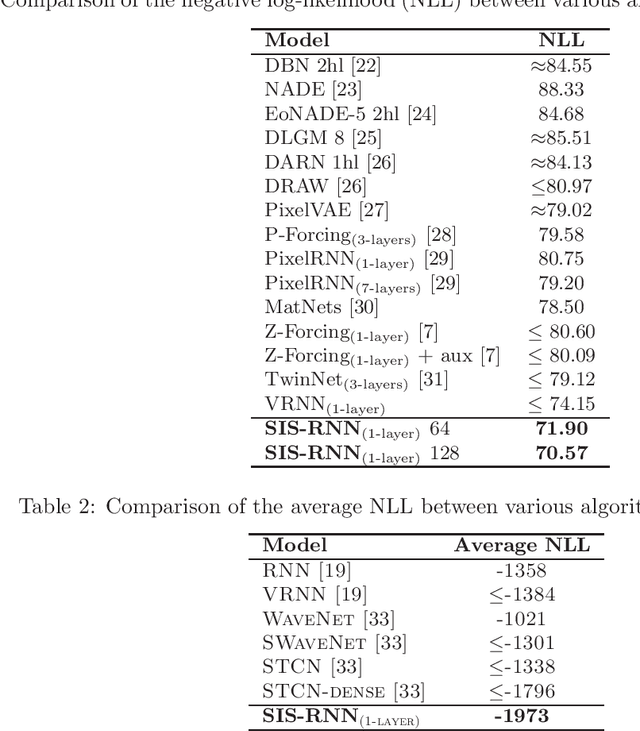
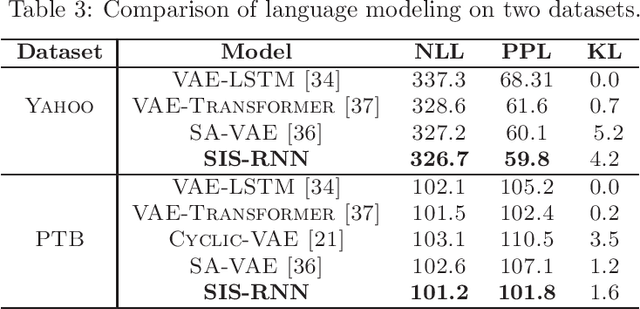
Stochastic recurrent neural networks with latent random variables of complex dependency structures have shown to be more successful in modeling sequential data than deterministic deep models. However, the majority of existing methods have limited expressive power due to the Gaussian assumption of latent variables. In this paper, we advocate learning implicit latent representations using semi-implicit variational inference to further increase model flexibility. Semi-implicit stochastic recurrent neural network(SIS-RNN) is developed to enrich inferred model posteriors that may have no analytic density functions, as long as independent random samples can be generated via reparameterization. Extensive experiments in different tasks on real-world datasets show that SIS-RNN outperforms the existing methods.

Temporal Network Sampling

Temporal networks representing a stream of timestamped edges are seemingly ubiquitous in the real-world. However, the massive size and continuous nature of these networks make them fundamentally challenging to analyze and leverage for descriptive and predictive modeling tasks. In this work, we propose a general framework for temporal network sampling with unbiased estimation. We develop online, single-pass sampling algorithms and unbiased estimators for temporal network sampling. The proposed algorithms enable fast, accurate, and memory-efficient statistical estimation of temporal network patterns and properties. In addition, we propose a temporally decaying sampling algorithm with unbiased estimators for studying networks that evolve in continuous time, where the strength of links is a function of time, and the motif patterns are temporally-weighted. In contrast to the prior notion of a $\bigtriangleup t$-temporal motif, the proposed formulation and algorithms for counting temporally weighted motifs are useful for forecasting tasks in networks such as predicting future links, or a future time-series variable of nodes and links. Finally, extensive experiments on a variety of temporal networks from different domains demonstrate the effectiveness of the proposed algorithms.