Bayesian Graph Contrastive Learning

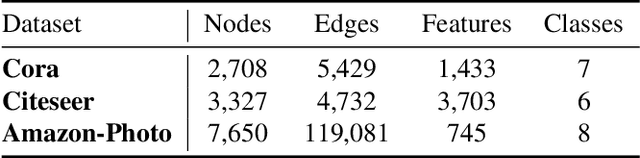
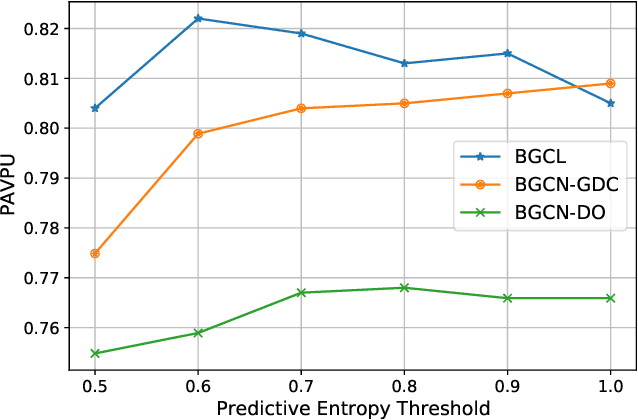
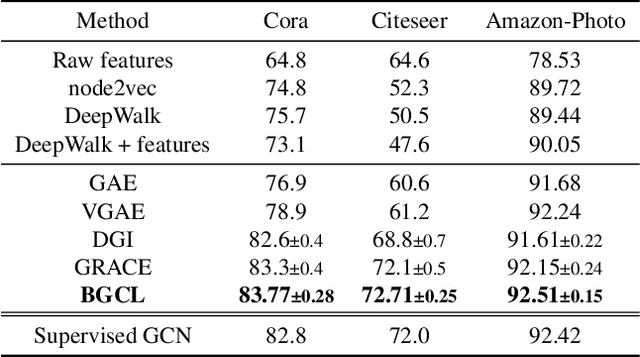
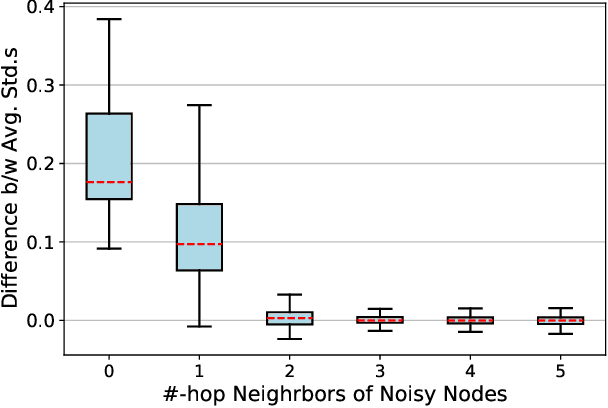
Contrastive learning has become a key component of self-supervised learning approaches for graph-structured data. However, despite their success, existing graph contrastive learning methods are incapable of uncertainty quantification for node representations or their downstream tasks, limiting their application in high-stakes domains. In this paper, we propose a novel Bayesian perspective of graph contrastive learning methods showing random augmentations leads to stochastic encoders. As a result, our proposed method represents each node by a distribution in the latent space in contrast to existing techniques which embed each node to a deterministic vector. By learning distributional representations, we provide uncertainty estimates in downstream graph analytics tasks and increase the expressive power of the predictive model. In addition, we propose a Bayesian framework to infer the probability of perturbations in each view of the contrastive model, eliminating the need for a computationally expensive search for hyperparameter tuning. We empirically show a considerable improvement in performance compared to existing state-of-the-art methods on several benchmark datasets.