Adaptive Conditional Quantile Neural Processes

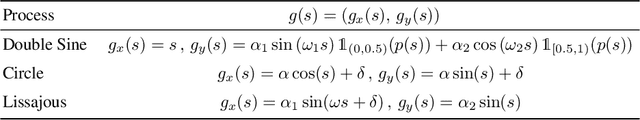
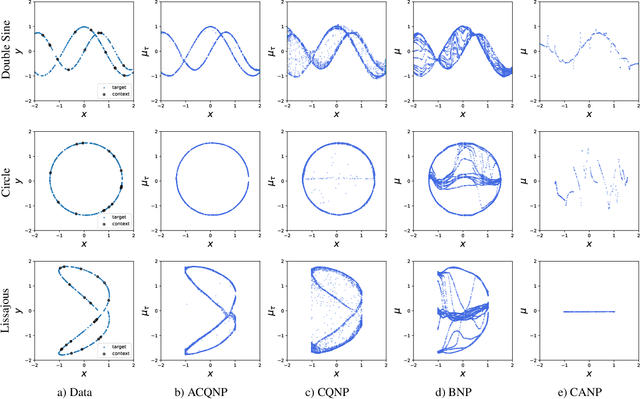
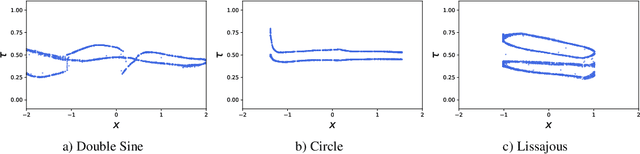
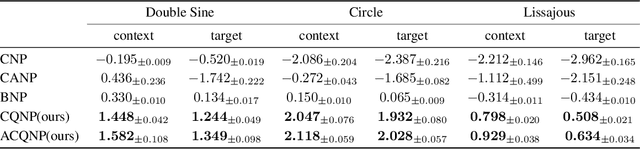
Neural processes are a family of probabilistic models that inherit the flexibility of neural networks to parameterize stochastic processes. Despite providing well-calibrated predictions, especially in regression problems, and quick adaptation to new tasks, the Gaussian assumption that is commonly used to represent the predictive likelihood fails to capture more complicated distributions such as multimodal ones. To overcome this limitation, we propose Conditional Quantile Neural Processes (CQNPs), a new member of the neural processes family, which exploits the attractive properties of quantile regression in modeling the distributions irrespective of their form. By introducing an extension of quantile regression where the model learns to focus on estimating informative quantiles, we show that the sampling efficiency and prediction accuracy can be further enhanced. Our experiments with real and synthetic datasets demonstrate substantial improvements in predictive performance compared to the baselines, and better modeling of heterogeneous distributions' characteristics such as multimodality.

MoReL: Multi-omics Relational Learning

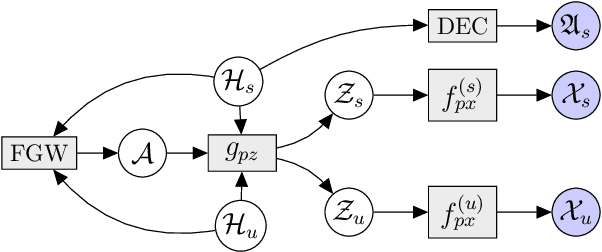
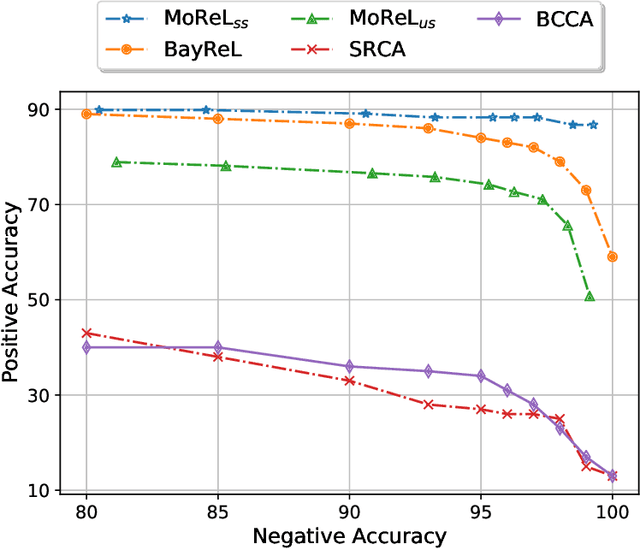
Multi-omics data analysis has the potential to discover hidden molecular interactions, revealing potential regulatory and/or signal transduction pathways for cellular processes of interest when studying life and disease systems. One of critical challenges when dealing with real-world multi-omics data is that they may manifest heterogeneous structures and data quality as often existing data may be collected from different subjects under different conditions for each type of omics data. We propose a novel deep Bayesian generative model to efficiently infer a multi-partite graph encoding molecular interactions across such heterogeneous views, using a fused Gromov-Wasserstein (FGW) regularization between latent representations of corresponding views for integrative analysis. With such an optimal transport regularization in the deep Bayesian generative model, it not only allows incorporating view-specific side information, either with graph-structured or unstructured data in different views, but also increases the model flexibility with the distribution-based regularization. This allows efficient alignment of heterogeneous latent variable distributions to derive reliable interaction predictions compared to the existing point-based graph embedding methods. Our experiments on several real-world datasets demonstrate enhanced performance of MoReL in inferring meaningful interactions compared to existing baselines.

Bayesian Graph Contrastive Learning

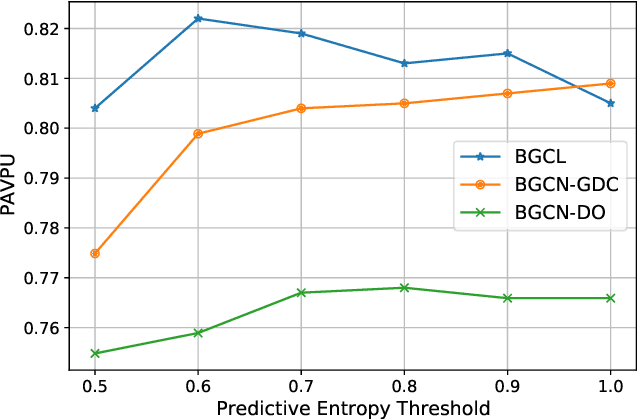
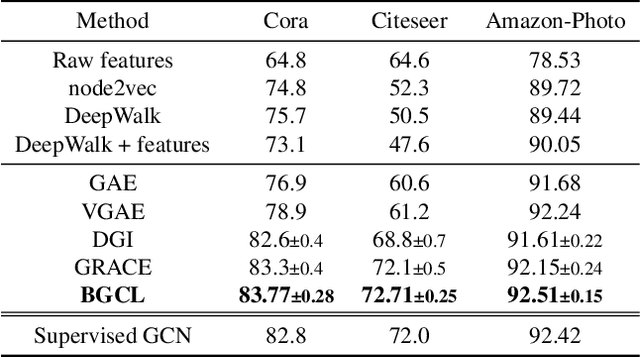
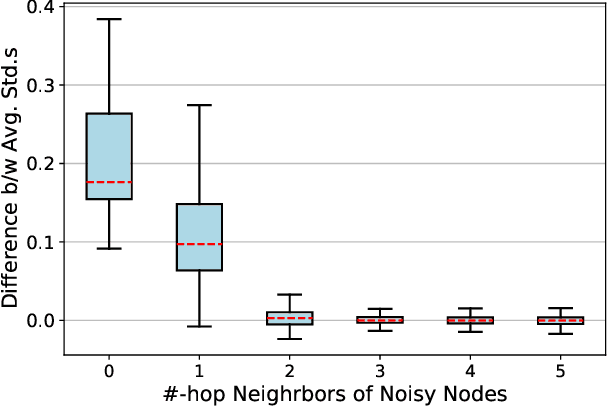
Contrastive learning has become a key component of self-supervised learning approaches for graph-structured data. However, despite their success, existing graph contrastive learning methods are incapable of uncertainty quantification for node representations or their downstream tasks, limiting their application in high-stakes domains. In this paper, we propose a novel Bayesian perspective of graph contrastive learning methods showing random augmentations leads to stochastic encoders. As a result, our proposed method represents each node by a distribution in the latent space in contrast to existing techniques which embed each node to a deterministic vector. By learning distributional representations, we provide uncertainty estimates in downstream graph analytics tasks and increase the expressive power of the predictive model. In addition, we propose a Bayesian framework to infer the probability of perturbations in each view of the contrastive model, eliminating the need for a computationally expensive search for hyperparameter tuning. We empirically show a considerable improvement in performance compared to existing state-of-the-art methods on several benchmark datasets.

BayReL: Bayesian Relational Learning for Multi-omics Data Integration

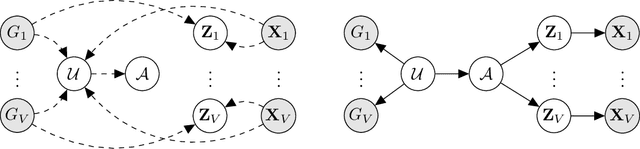
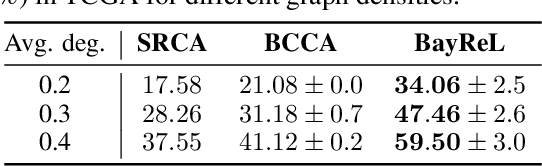
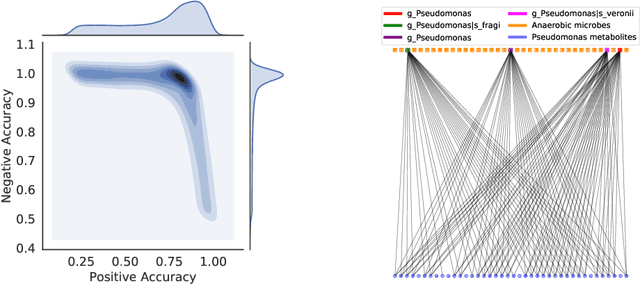
High-throughput molecular profiling technologies have produced high-dimensional multi-omics data, enabling systematic understanding of living systems at the genome scale. Studying molecular interactions across different data types helps reveal signal transduction mechanisms across different classes of molecules. In this paper, we develop a novel Bayesian representation learning method that infers the relational interactions across multi-omics data types. Our method, Bayesian Relational Learning (BayReL) for multi-omics data integration, takes advantage of a priori known relationships among the same class of molecules, modeled as a graph at each corresponding view, to learn view-specific latent variables as well as a multi-partite graph that encodes the interactions across views. Our experiments on several real-world datasets demonstrate enhanced performance of BayReL in inferring meaningful interactions compared to existing baselines.

Bayesian Graph Neural Networks with Adaptive Connection Sampling

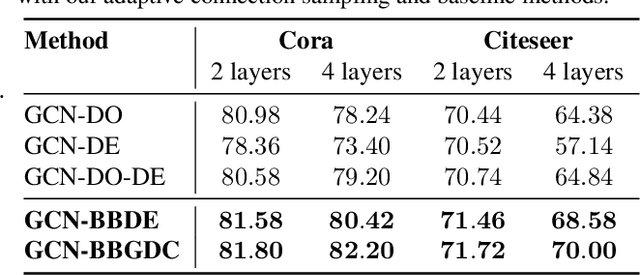
We propose a unified framework for adaptive connection sampling in graph neural networks (GNNs) that generalizes existing stochastic regularization methods for training GNNs. The proposed framework not only alleviates over-smoothing and over-fitting tendencies of deep GNNs, but also enables learning with uncertainty in graph analytic tasks with GNNs. Instead of using fixed sampling rates or hand-tuning them as model hyperparameters in existing stochastic regularization methods, our adaptive connection sampling can be trained jointly with GNN model parameters in both global and local fashions. GNN training with adaptive connection sampling is shown to be mathematically equivalent to an efficient approximation of training Bayesian GNNs. Experimental results with ablation studies on benchmark datasets validate that adaptively learning the sampling rate given graph training data is the key to boost the performance of GNNs in semi-supervised node classification, less prone to over-smoothing and over-fitting with more robust prediction.

Network-principled deep generative models for designing drug combinations as graph sets

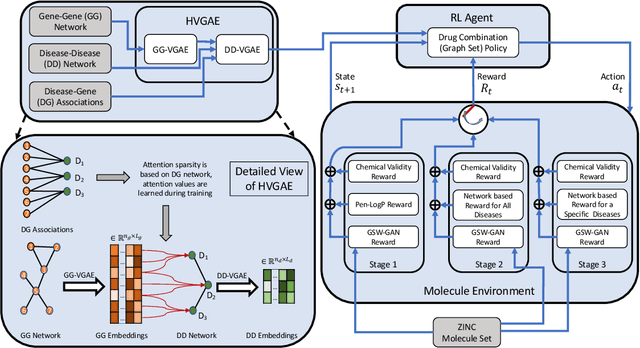
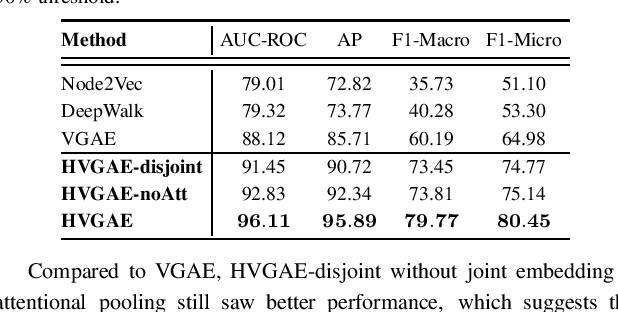
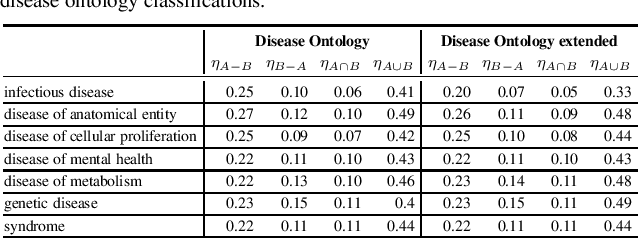
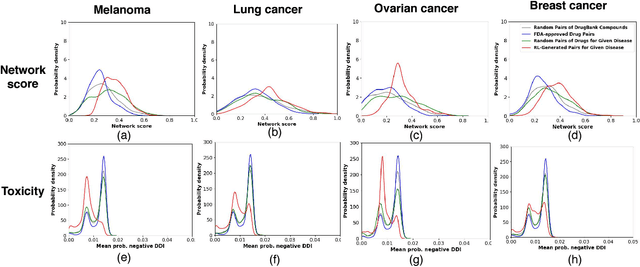
Combination therapy has shown to improve therapeutic efficacy while reducing side effects. Importantly, it has become an indispensable strategy to overcome resistance in antibiotics, anti-microbials, and anti-cancer drugs. Facing enormous chemical space and unclear design principles for small-molecule combinations, the computational drug-combination design has not seen generative models to meet its potential to accelerate resistance-overcoming drug combination discovery. We have developed the first deep generative model for drug combination design, by jointly embedding graph-structured domain knowledge and iteratively training a reinforcement learning-based chemical graph-set designer. First, we have developed Hierarchical Variational Graph Auto-Encoders (HVGAE) trained end-to-end to jointly embed gene-gene, gene-disease, and disease-disease networks. Novel attentional pooling is introduced here for learning disease-representations from associated genes' representations. Second, targeting diseases in learned representations, we have recast the drug-combination design problem as graph-set generation and developed a deep learning-based model with novel rewards. Specifically, besides chemical validity rewards, we have introduced a novel generative adversarial award, being generalized sliced Wasserstein, for chemically diverse molecules with distributions similar to known drugs. We have also designed a network principle-based reward for drug combinations. Numerical results indicate that, compared to graph embedding methods, HVGAE learns more informative and generalizable disease representations. Case studies on four diseases show that network-principled drug combinations tend to have low toxicity. The generated drug combinations collectively cover the disease module similar to FDA-approved drug combinations and could potentially suggest novel systems-pharmacology strategies.

Semi-Implicit Stochastic Recurrent Neural Networks

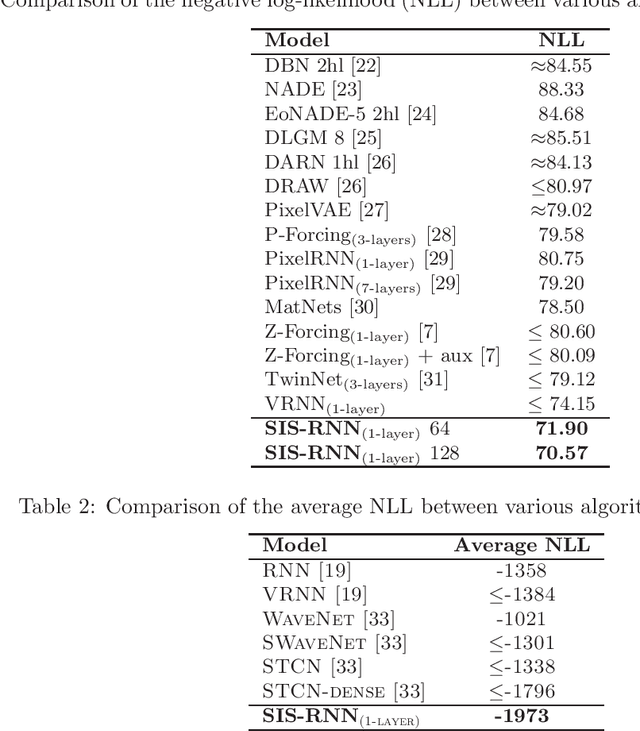
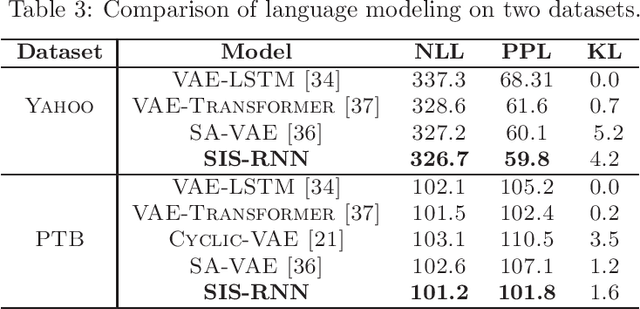
Stochastic recurrent neural networks with latent random variables of complex dependency structures have shown to be more successful in modeling sequential data than deterministic deep models. However, the majority of existing methods have limited expressive power due to the Gaussian assumption of latent variables. In this paper, we advocate learning implicit latent representations using semi-implicit variational inference to further increase model flexibility. Semi-implicit stochastic recurrent neural network(SIS-RNN) is developed to enrich inferred model posteriors that may have no analytic density functions, as long as independent random samples can be generated via reparameterization. Extensive experiments in different tasks on real-world datasets show that SIS-RNN outperforms the existing methods.

Variational Graph Recurrent Neural Networks

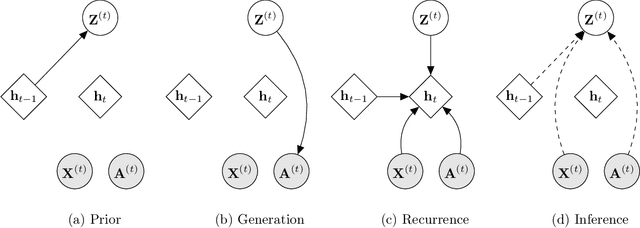
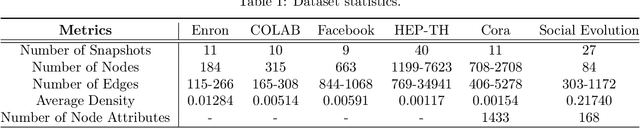
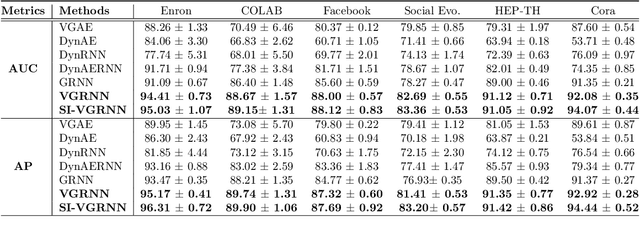
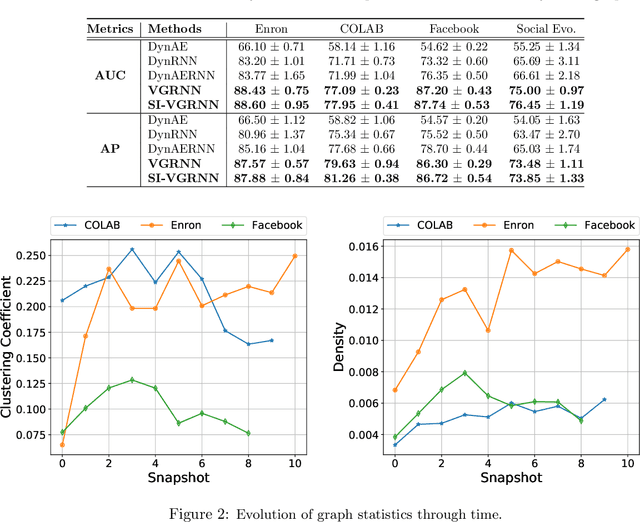
Representation learning over graph structured data has been mostly studied in static graph settings while efforts for modeling dynamic graphs are still scant. In this paper, we develop a novel hierarchical variational model that introduces additional latent random variables to jointly model the hidden states of a graph recurrent neural network (GRNN) to capture both topology and node attribute changes in dynamic graphs. We argue that the use of high-level latent random variables in this variational GRNN (VGRNN) can better capture potential variability observed in dynamic graphs as well as the uncertainty of node latent representation. With semi-implicit variational inference developed for this new VGRNN architecture (SI-VGRNN), we show that flexible non-Gaussian latent representations can further help dynamic graph analytic tasks. Our experiments with multiple real-world dynamic graph datasets demonstrate that SI-VGRNN and VGRNN consistently outperform the existing baseline and state-of-the-art methods by a significant margin in dynamic link prediction.

Semi-Implicit Graph Variational Auto-Encoders

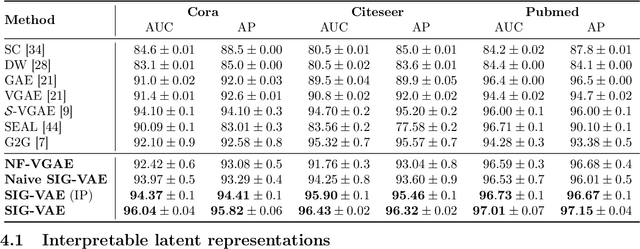
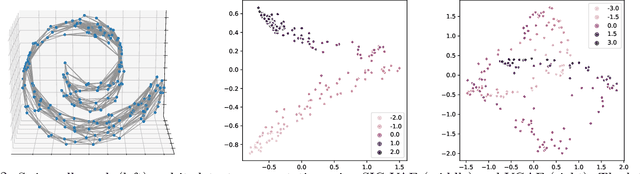
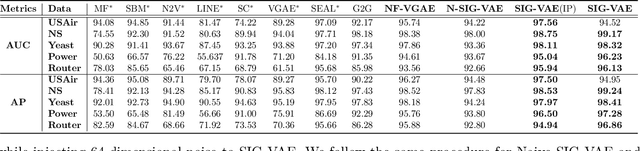
Semi-implicit graph variational auto-encoder (SIG-VAE) is proposed to expand the flexibility of variational graph auto-encoders (VGAE) to model graph data. SIG-VAE employs a hierarchical variational framework to enable neighboring node sharing for better generative modeling of graph dependency structure, together with a Bernoulli-Poisson link decoder. Not only does this hierarchical construction provide a more flexible generative graph model to better capture real-world graph properties, but also does SIG-VAE naturally lead to semi-implicit hierarchical variational inference that allows faithful modeling of implicit posteriors of given graph data, which may exhibit heavy tails, multiple modes, skewness, and rich dependency structures. Compared to VGAE, the derived graph latent representations by SIG-VAE are more interpretable, due to more expressive generative model and more faithful inference enabled by the flexible semi-implicit construction. Extensive experiments with a variety of graph data show that SIG-VAE significantly outperforms state-of-the-art methods on several different graph analytic tasks.

Spatially-Coupled Neural Network Architectures

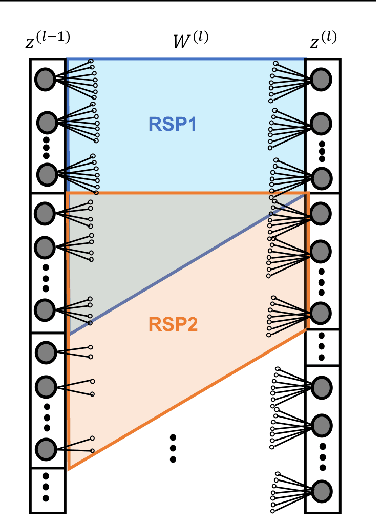
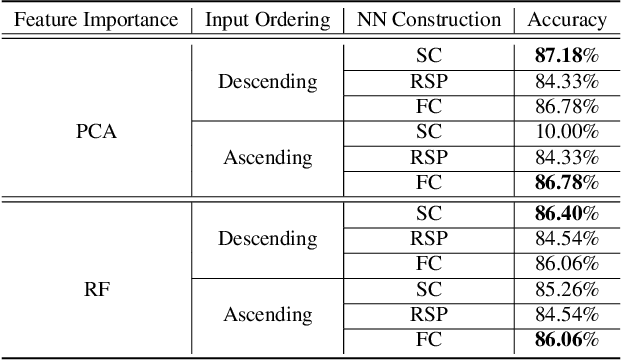
In this work, we leverage advances in sparse coding techniques to reduce the number of trainable parameters in a fully connected neural network. While most of the works in literature impose $\ell_1$ regularization, DropOut or DropConnect techniques to induce sparsity, our scheme considers feature importance as a criterion to allocate the trainable parameters (resources) efficiently in the network. Even though sparsity is ensured, $\ell_1$ regularization requires training on all the resources in a deep neural network. The DropOut/DropConnect techniques reduce the number of trainable parameters in the training stage by dropping a random collection of neurons/edges in the hidden layers. However, both these techniques do not pay heed to the underlying structure in the data when dropping the neurons/edges. Moreover, these frameworks require a storage space equivalent to the number of parameters in a fully connected neural network. We address the above issues with a more structured architecture inspired from spatially-coupled sparse constructions. The proposed architecture is shown to have a performance akin to a conventional fully connected neural network with dropouts, and yet achieving a $94\%$ reduction in the training parameters. Extensive simulations are presented and the performance of the proposed scheme is compared against traditional neural network architectures.