QoS-Efficient Serving of Multiple Mixture-of-Expert LLMs Using Partial Runtime Reconfiguration

The deployment of mixture-of-experts (MoE) large language models (LLMs) presents significant challenges due to their high memory demands. These challenges become even more pronounced in multi-tenant environments, where shared resources must accommodate multiple models, limiting the effectiveness of conventional virtualization techniques. This paper addresses the problem of efficiently serving multiple fine-tuned MoE-LLMs on a single-GPU. We propose a serving system that employs \textit{similarity-based expert consolidation} to reduce the overall memory footprint by sharing similar experts across models. To ensure output quality, we introduce \textit{runtime partial reconfiguration}, dynamically replacing non-expert layers when processing requests from different models. As a result, our approach achieves a competitive output quality while maintaining throughput comparable to serving a single model while incurring a negligible increase in time-to-first-token (TTFT). Experiments on a server with a single NVIDIA A100 GPU (80GB) using Mixtral-8x7B models demonstrate an 85\% average reduction in turnaround time compared to NVIDIA's multi-instance GPU (MIG). Furthermore, experiments on Google's Switch Transformer Base-8 model with up to four variants demonstrate the scalability and resilience of our approach in maintaining output quality compared to other model merging baselines, highlighting its effectiveness.

Spectral Convolutional Conditional Neural Processes

Conditional Neural Processes (CNPs) constitute a family of probabilistic models that harness the flexibility of neural networks to parameterize stochastic processes. Their capability to furnish well-calibrated predictions, combined with simple maximum-likelihood training, has established them as appealing solutions for addressing various learning problems, with a particular emphasis on meta-learning. A prominent member of this family, Convolutional Conditional Neural Processes (ConvCNPs), utilizes convolution to explicitly introduce translation equivariance as an inductive bias. However, ConvCNP's reliance on local discrete kernels in its convolution layers can pose challenges in capturing long-range dependencies and complex patterns within the data, especially when dealing with limited and irregularly sampled observations from a new task. Building on the successes of Fourier neural operators (FNOs) for approximating the solution operators of parametric partial differential equations (PDEs), we propose Spectral Convolutional Conditional Neural Processes (SConvCNPs), a new addition to the NPs family that allows for more efficient representation of functions in the frequency domain.

Adaptive Conditional Quantile Neural Processes

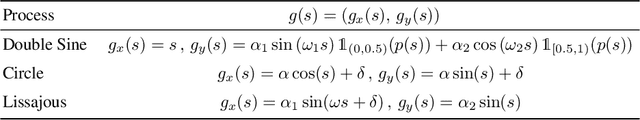
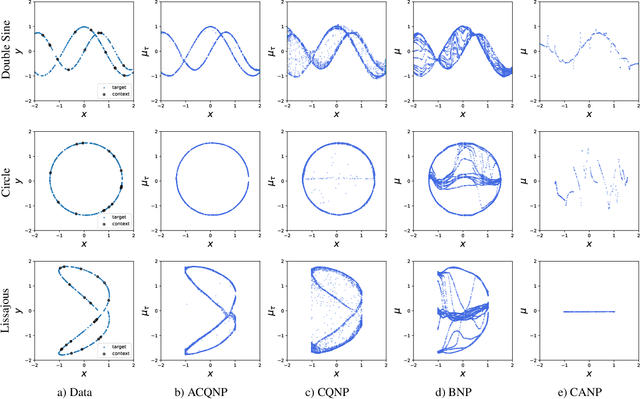
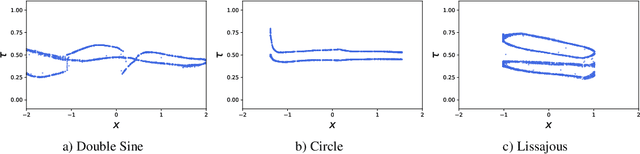
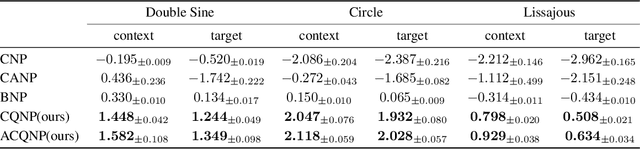
Neural processes are a family of probabilistic models that inherit the flexibility of neural networks to parameterize stochastic processes. Despite providing well-calibrated predictions, especially in regression problems, and quick adaptation to new tasks, the Gaussian assumption that is commonly used to represent the predictive likelihood fails to capture more complicated distributions such as multimodal ones. To overcome this limitation, we propose Conditional Quantile Neural Processes (CQNPs), a new member of the neural processes family, which exploits the attractive properties of quantile regression in modeling the distributions irrespective of their form. By introducing an extension of quantile regression where the model learns to focus on estimating informative quantiles, we show that the sampling efficiency and prediction accuracy can be further enhanced. Our experiments with real and synthetic datasets demonstrate substantial improvements in predictive performance compared to the baselines, and better modeling of heterogeneous distributions' characteristics such as multimodality.