Transformers as Unsupervised Learning Algorithms: A study on Gaussian Mixtures

The transformer architecture has demonstrated remarkable capabilities in modern artificial intelligence, among which the capability of implicitly learning an internal model during inference time is widely believed to play a key role in the under standing of pre-trained large language models. However, most recent works have been focusing on studying supervised learning topics such as in-context learning, leaving the field of unsupervised learning largely unexplored. This paper investigates the capabilities of transformers in solving Gaussian Mixture Models (GMMs), a fundamental unsupervised learning problem through the lens of statistical estimation. We propose a transformer-based learning framework called TGMM that simultaneously learns to solve multiple GMM tasks using a shared transformer backbone. The learned models are empirically demonstrated to effectively mitigate the limitations of classical methods such as Expectation-Maximization (EM) or spectral algorithms, at the same time exhibit reasonable robustness to distribution shifts. Theoretically, we prove that transformers can approximate both the EM algorithm and a core component of spectral methods (cubic tensor power iterations). These results bridge the gap between practical success and theoretical understanding, positioning transformers as versatile tools for unsupervised learning.

Learning under Commission and Omission Event Outliers

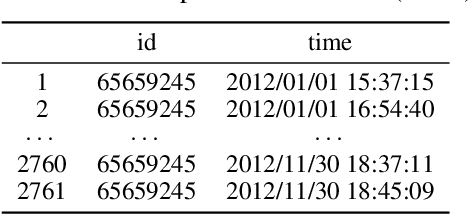
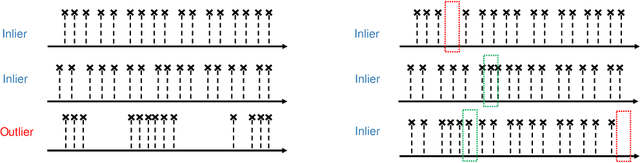
Event stream is an important data format in real life. The events are usually expected to follow some regular patterns over time. However, the patterns could be contaminated by unexpected absences or occurrences of events. In this paper, we adopt the temporal point process framework for learning event stream and we provide a simple-but-effective method to deal with both commission and omission event outliers.In particular, we introduce a novel weight function to dynamically adjust the importance of each observed event so that the final estimator could offer multiple statistical merits. We compare the proposed method with the vanilla one in the classification problems, where event streams can be clustered into different groups. Both theoretical and numerical results confirm the effectiveness of our new approach. To our knowledge, our method is the first one to provably handle both commission and omission outliers simultaneously.

On Non-asymptotic Theory of Recurrent Neural Networks in Temporal Point Processes

Temporal point process (TPP) is an important tool for modeling and predicting irregularly timed events across various domains. Recently, the recurrent neural network (RNN)-based TPPs have shown practical advantages over traditional parametric TPP models. However, in the current literature, it remains nascent in understanding neural TPPs from theoretical viewpoints. In this paper, we establish the excess risk bounds of RNN-TPPs under many well-known TPP settings. We especially show that an RNN-TPP with no more than four layers can achieve vanishing generalization errors. Our technical contributions include the characterization of the complexity of the multi-layer RNN class, the construction of $\tanh$ neural networks for approximating dynamic event intensity functions, and the truncation technique for alleviating the issue of unbounded event sequences. Our results bridge the gap between TPP's application and neural network theory.

On provable privacy vulnerabilities of graph representations

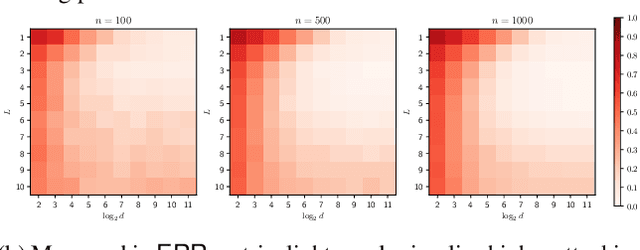
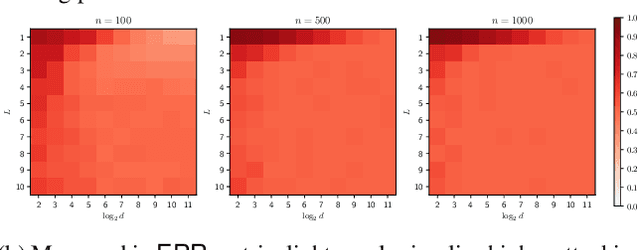
Graph representation learning (GRL) is critical for extracting insights from complex network structures, but it also raises security concerns due to potential privacy vulnerabilities in these representations. This paper investigates the structural vulnerabilities in graph neural models where sensitive topological information can be inferred through edge reconstruction attacks. Our research primarily addresses the theoretical underpinnings of cosine-similarity-based edge reconstruction attacks (COSERA), providing theoretical and empirical evidence that such attacks can perfectly reconstruct sparse Erdos Renyi graphs with independent random features as graph size increases. Conversely, we establish that sparsity is a critical factor for COSERA's effectiveness, as demonstrated through analysis and experiments on stochastic block models. Finally, we explore the resilience of (provably) private graph representations produced via noisy aggregation (NAG) mechanism against COSERA. We empirically delineate instances wherein COSERA demonstrates both efficacy and deficiency in its capacity to function as an instrument for elucidating the trade-off between privacy and utility.

Empirical Risk Minimization for Losses without Variance

This paper considers an empirical risk minimization problem under heavy-tailed settings, where data does not have finite variance, but only has $p$-th moment with $p \in (1,2)$. Instead of using estimation procedure based on truncated observed data, we choose the optimizer by minimizing the risk value. Those risk values can be robustly estimated via using the remarkable Catoni's method (Catoni, 2012). Thanks to the structure of Catoni-type influence functions, we are able to establish excess risk upper bounds via using generalized generic chaining methods. Moreover, we take computational issues into consideration. We especially theoretically investigate two types of optimization methods, robust gradient descent algorithm and empirical risk-based methods. With an extensive numerical study, we find that the optimizer based on empirical risks via Catoni-style estimation indeed shows better performance than other baselines. It indicates that estimation directly based on truncated data may lead to unsatisfactory results.

Copula for Instance-wise Feature Selection and Ranking

Instance-wise feature selection and ranking methods can achieve a good selection of task-friendly features for each sample in the context of neural networks. However, existing approaches that assume feature subsets to be independent are imperfect when considering the dependency between features. To address this limitation, we propose to incorporate the Gaussian copula, a powerful mathematical technique for capturing correlations between variables, into the current feature selection framework with no additional changes needed. Experimental results on both synthetic and real datasets, in terms of performance comparison and interpretability, demonstrate that our method is capable of capturing meaningful correlations.

A Cover Time Study of a non-Markovian Algorithm

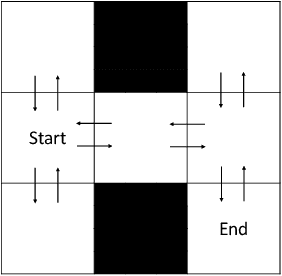
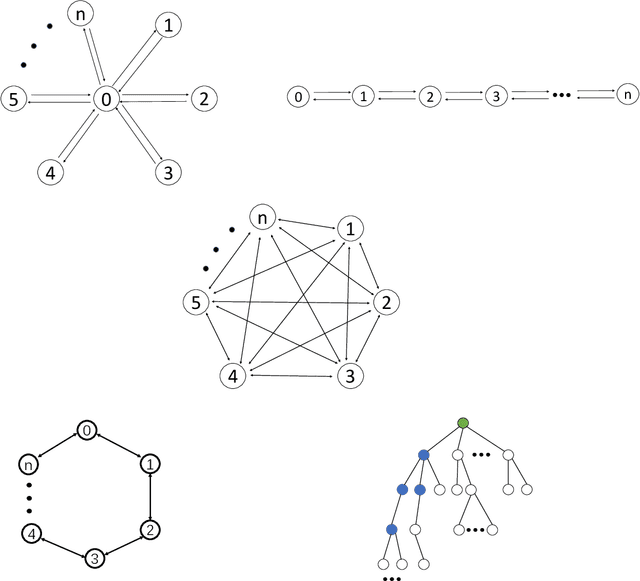
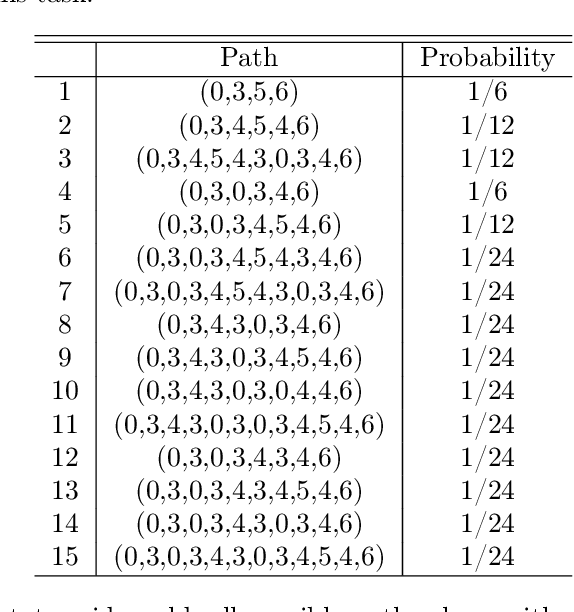
Given a traversal algorithm, cover time is the expected number of steps needed to visit all nodes in a given graph. A smaller cover time means a higher exploration efficiency of traversal algorithm. Although random walk algorithms have been studied extensively in the existing literature, there has been no cover time result for any non-Markovian method. In this work, we stand on a theoretical perspective and show that the negative feedback strategy (a count-based exploration method) is better than the naive random walk search. In particular, the former strategy can locally improve the search efficiency for an arbitrary graph. It also achieves smaller cover times for special but important graphs, including clique graphs, tree graphs, etc. Moreover, we make connections between our results and reinforcement learning literature to give new insights on why classical UCB and MCTS algorithms are so useful. Various numerical results corroborate our theoretical findings.

On Penalization in Stochastic Multi-armed Bandits

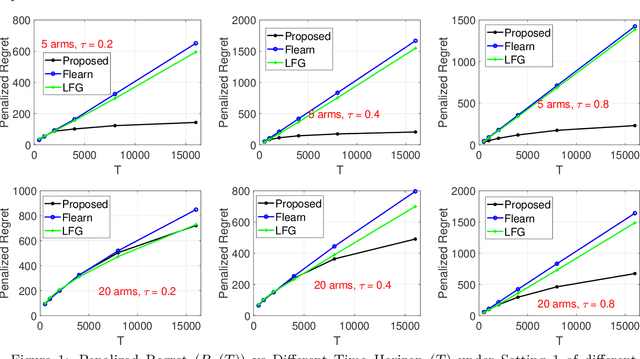
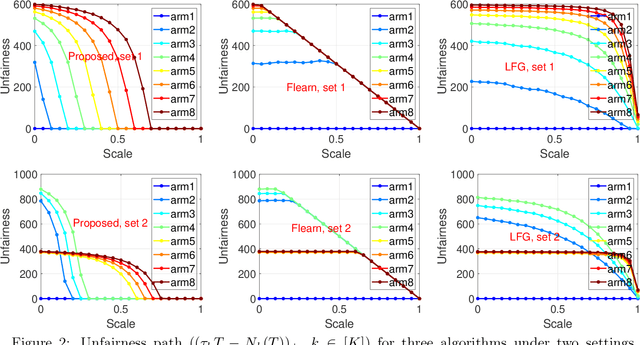
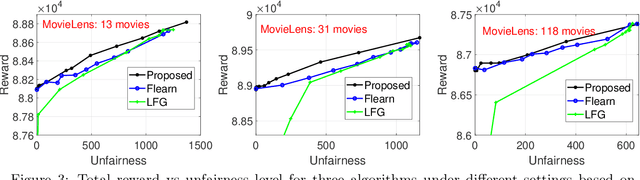
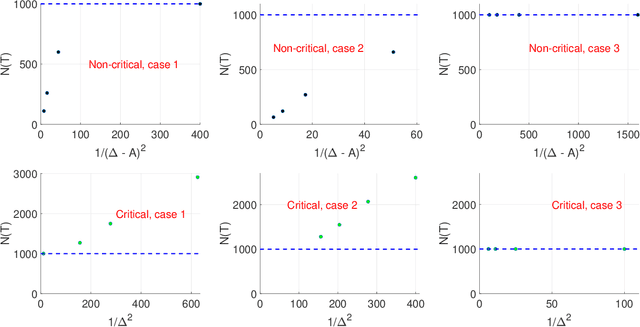
We study an important variant of the stochastic multi-armed bandit (MAB) problem, which takes penalization into consideration. Instead of directly maximizing cumulative expected reward, we need to balance between the total reward and fairness level. In this paper, we present some new insights in MAB and formulate the problem in the penalization framework, where rigorous penalized regret can be well defined and more sophisticated regret analysis is possible. Under such a framework, we propose a hard-threshold UCB-like algorithm, which enjoys many merits including asymptotic fairness, nearly optimal regret, better tradeoff between reward and fairness. Both gap-dependent and gap-independent regret bounds have been established. Multiple insightful comments are given to illustrate the soundness of our theoretical analysis. Numerous experimental results corroborate the theory and show the superiority of our method over other existing methods.

Catoni-style Confidence Sequences under Infinite Variance

In this paper, we provide an extension of confidence sequences for settings where the variance of the data-generating distribution does not exist or is infinite. Confidence sequences furnish confidence intervals that are valid at arbitrary data-dependent stopping times, naturally having a wide range of applications. We first establish a lower bound for the width of the Catoni-style confidence sequences for the finite variance case to highlight the looseness of the existing results. Next, we derive tight Catoni-style confidence sequences for data distributions having a relaxed bounded~$p^{th}-$moment, where~$p \in (1,2]$, and strengthen the results for the finite variance case of~$p =2$. The derived results are shown to better than confidence sequences obtained using Dubins-Savage inequality.

Best Subset Selection with Efficient Primal-Dual Algorithm

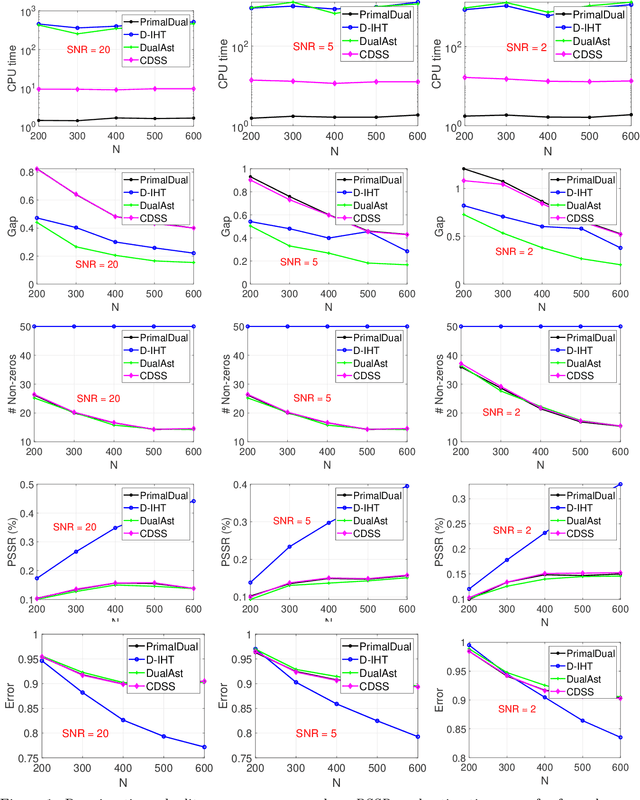
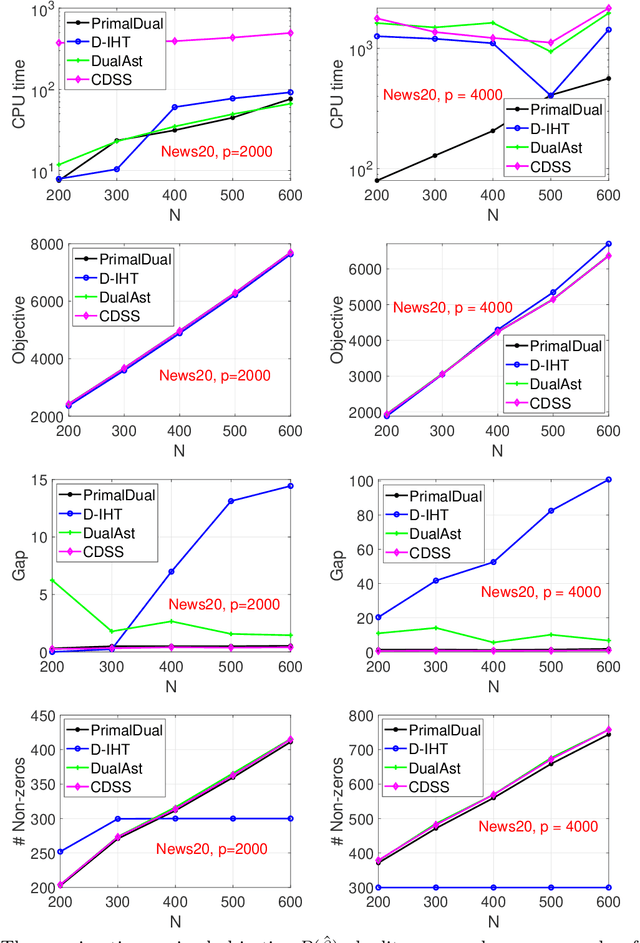
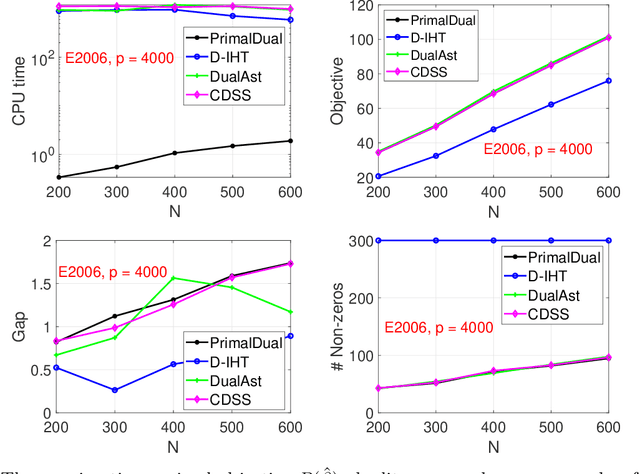
Best subset selection is considered the `gold standard' for many sparse learning problems. A variety of optimization techniques have been proposed to attack this non-convex and NP-hard problem. In this paper, we investigate the dual forms of a family of $\ell_0$-regularized problems. An efficient primal-dual method has been developed based on the primal and dual problem structures. By leveraging the dual range estimation along with the incremental strategy, our algorithm potentially reduces redundant computation and improves the solutions of best subset selection. Theoretical analysis and experiments on synthetic and real-world datasets validate the efficiency and statistical properties of the proposed solutions.