On Penalization in Stochastic Multi-armed Bandits
Paper and Code
Nov 15, 2022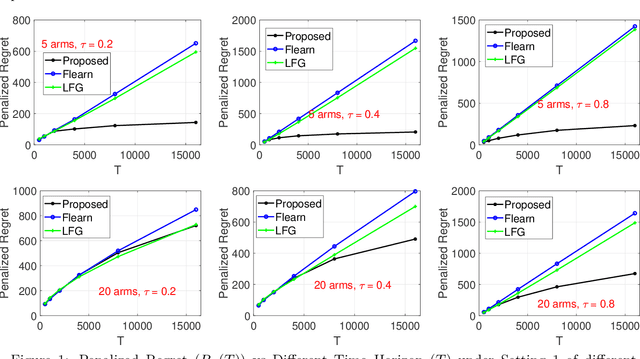
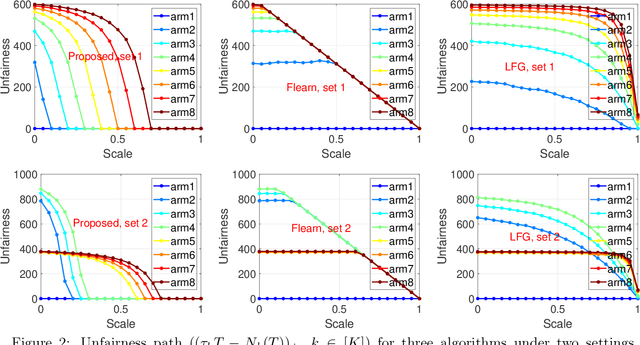
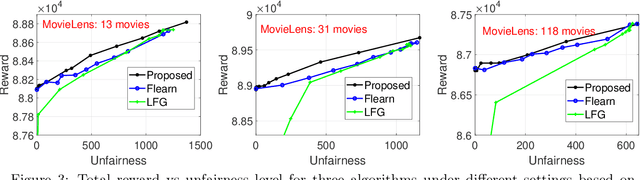
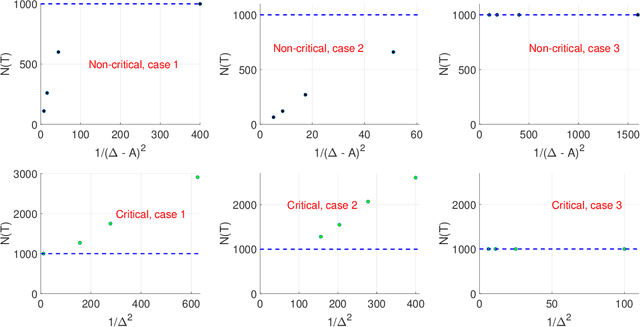
We study an important variant of the stochastic multi-armed bandit (MAB) problem, which takes penalization into consideration. Instead of directly maximizing cumulative expected reward, we need to balance between the total reward and fairness level. In this paper, we present some new insights in MAB and formulate the problem in the penalization framework, where rigorous penalized regret can be well defined and more sophisticated regret analysis is possible. Under such a framework, we propose a hard-threshold UCB-like algorithm, which enjoys many merits including asymptotic fairness, nearly optimal regret, better tradeoff between reward and fairness. Both gap-dependent and gap-independent regret bounds have been established. Multiple insightful comments are given to illustrate the soundness of our theoretical analysis. Numerous experimental results corroborate the theory and show the superiority of our method over other existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge