Marc Lavielle
On the Global Convergence of (Fast) Incremental Expectation Maximization Methods
Oct 28, 2019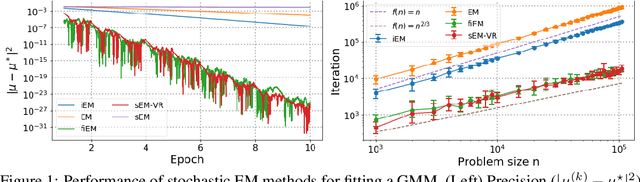
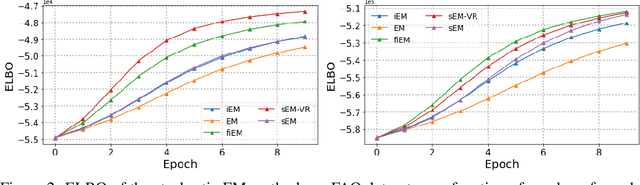
Abstract:The EM algorithm is one of the most popular algorithm for inference in latent data models. The original formulation of the EM algorithm does not scale to large data set, because the whole data set is required at each iteration of the algorithm. To alleviate this problem, Neal and Hinton have proposed an incremental version of the EM (iEM) in which at each iteration the conditional expectation of the latent data (E-step) is updated only for a mini-batch of observations. Another approach has been proposed by Capp\'e and Moulines in which the E-step is replaced by a stochastic approximation step, closely related to stochastic gradient. In this paper, we analyze incremental and stochastic version of the EM algorithm as well as the variance reduced-version of Chen et. al. in a common unifying framework. We also introduce a new version incremental version, inspired by the SAGA algorithm by Defazio et. al. We establish non-asymptotic convergence bounds for global convergence. Numerical applications are presented in this article to illustrate our findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge