A Class of Two-Timescale Stochastic EM Algorithms for Nonconvex Latent Variable Models
Paper and Code
Mar 18, 2022
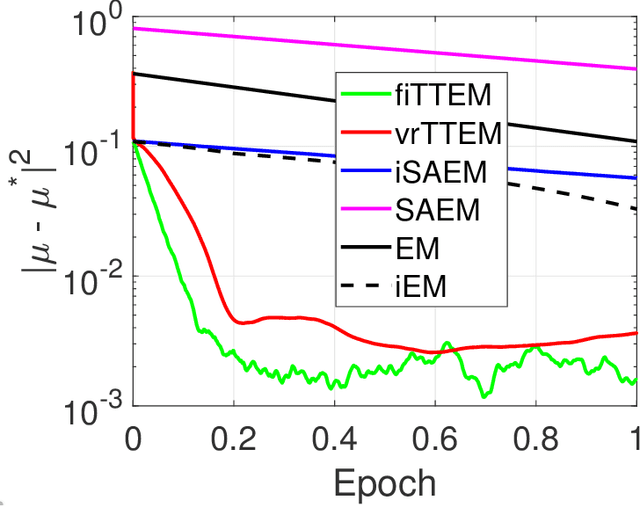


The Expectation-Maximization (EM) algorithm is a popular choice for learning latent variable models. Variants of the EM have been initially introduced, using incremental updates to scale to large datasets, and using Monte Carlo (MC) approximations to bypass the intractable conditional expectation of the latent data for most nonconvex models. In this paper, we propose a general class of methods called Two-Timescale EM Methods based on a two-stage approach of stochastic updates to tackle an essential nonconvex optimization task for latent variable models. We motivate the choice of a double dynamic by invoking the variance reduction virtue of each stage of the method on both sources of noise: the index sampling for the incremental update and the MC approximation. We establish finite-time and global convergence bounds for nonconvex objective functions. Numerical applications on various models such as deformable template for image analysis or nonlinear models for pharmacokinetics are also presented to illustrate our findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge