Enhancing Language Learning through Technology: Introducing a New English-Azerbaijani (Arabic Script) Parallel Corpus

This paper introduces a pioneering English-Azerbaijani (Arabic Script) parallel corpus, designed to bridge the technological gap in language learning and machine translation (MT) for under-resourced languages. Consisting of 548,000 parallel sentences and approximately 9 million words per language, this dataset is derived from diverse sources such as news articles and holy texts, aiming to enhance natural language processing (NLP) applications and language education technology. This corpus marks a significant step forward in the realm of linguistic resources, particularly for Turkic languages, which have lagged in the neural machine translation (NMT) revolution. By presenting the first comprehensive case study for the English-Azerbaijani (Arabic Script) language pair, this work underscores the transformative potential of NMT in low-resource contexts. The development and utilization of this corpus not only facilitate the advancement of machine translation systems tailored for specific linguistic needs but also promote inclusive language learning through technology. The findings demonstrate the corpus's effectiveness in training deep learning MT systems and underscore its role as an essential asset for researchers and educators aiming to foster bilingual education and multilingual communication. This research covers the way for future explorations into NMT applications for languages lacking substantial digital resources, thereby enhancing global language education frameworks. The Python package of our code is available at https://pypi.org/project/chevir-kartalol/, and we also have a website accessible at https://translate.kartalol.com/.

KartalOl: Transfer learning using deep neural network for iris segmentation and localization: New dataset for iris segmentation

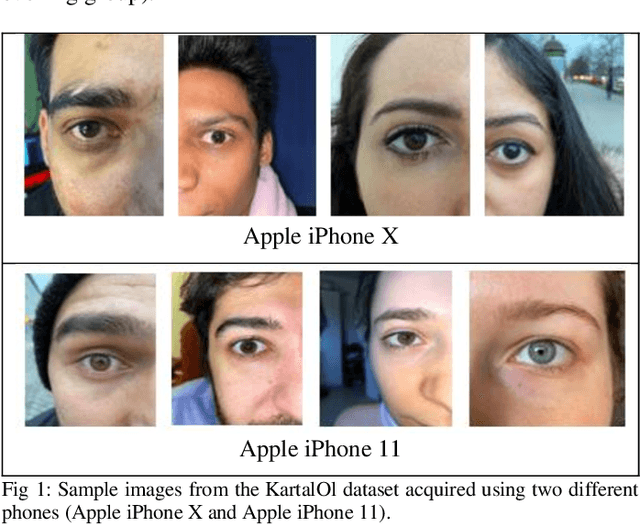
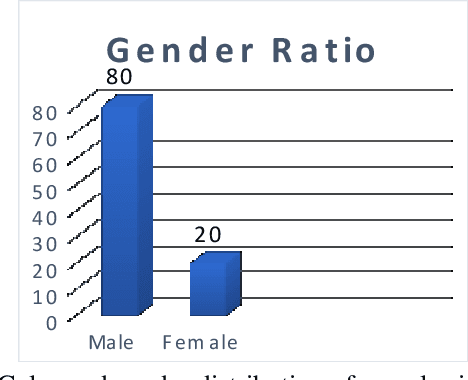
Iris segmentation and localization in unconstrained environments is challenging due to long distances, illumination variations, limited user cooperation, and moving subjects. To address this problem, we present a U-Net with a pre-trained MobileNetV2 deep neural network method. We employ the pre-trained weights given with MobileNetV2 for the ImageNet dataset and fine-tune it on the iris recognition and localization domain. Further, we have introduced a new dataset, called KartalOl, to better evaluate detectors in iris recognition scenarios. To provide domain adaptation, we fine-tune the MobileNetV2 model on the provided data for NIR-ISL 2021 from the CASIA-Iris-Asia, CASIA-Iris-M1, and CASIA-Iris-Africa and our dataset. We also augment the data by performing left-right flips, rotation, zoom, and brightness. We chose the binarization threshold for the binary masks by iterating over the images in the provided dataset. The proposed method is tested and trained in CASIA-Iris-Asia, CASIA-Iris-M1, CASIA-Iris-Africa, along the KartalOl dataset. The experimental results highlight that our method surpasses state-of-the-art methods on mobile-based benchmarks. The codes and evaluation results are publicly available at https://github.com/Jalilnkh/KartalOl-NIR-ISL2021031301.

Clinical Recommender System: Predicting Medical Specialty Diagnostic Choices with Neural Network Ensembles

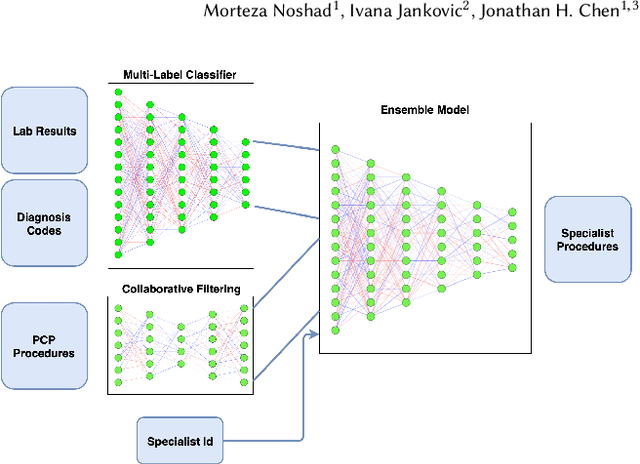
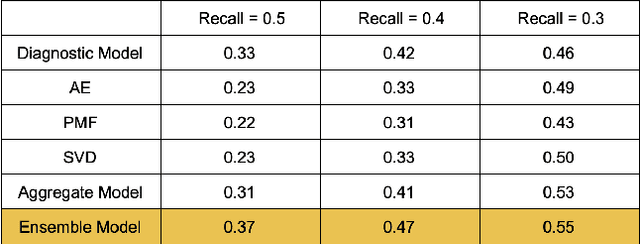
The growing demand for key healthcare resources such as clinical expertise and facilities has motivated the emergence of artificial intelligence (AI) based decision support systems. We address the problem of predicting clinical workups for specialty referrals. As an alternative for manually-created clinical checklists, we propose a data-driven model that recommends the necessary set of diagnostic procedures based on the patients' most recent clinical record extracted from the Electronic Health Record (EHR). This has the potential to enable health systems expand timely access to initial medical specialty diagnostic workups for patients. The proposed approach is based on an ensemble of feed-forward neural networks and achieves significantly higher accuracy compared to the conventional clinical checklists.

Learning to Benchmark: Determining Best Achievable Misclassification Error from Training Data

We address the problem of learning to benchmark the best achievable classifier performance. In this problem the objective is to establish statistically consistent estimates of the Bayes misclassification error rate without having to learn a Bayes-optimal classifier. Our learning to benchmark framework improves on previous work on learning bounds on Bayes misclassification rate since it learns the {\it exact} Bayes error rate instead of a bound on error rate. We propose a benchmark learner based on an ensemble of $\epsilon$-ball estimators and Chebyshev approximation. Under a smoothness assumption on the class densities we show that our estimator achieves an optimal (parametric) mean squared error (MSE) rate of $O(N^{-1})$, where $N$ is the number of samples. Experiments on both simulated and real datasets establish that our proposed benchmark learning algorithm produces estimates of the Bayes error that are more accurate than previous approaches for learning bounds on Bayes error probability.

Convergence Rates for Empirical Estimation of Binary Classification Bounds

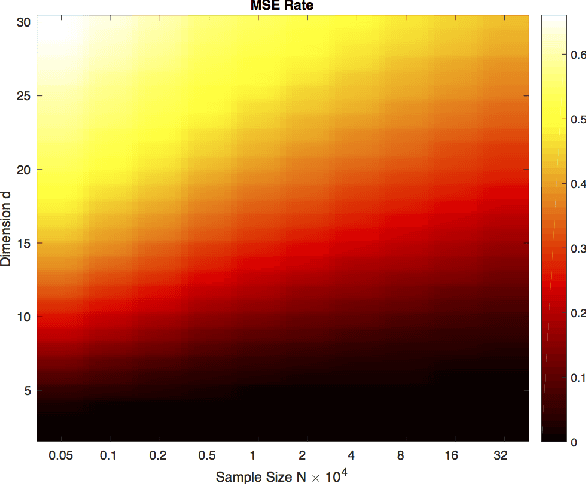
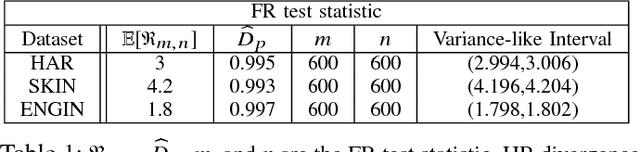
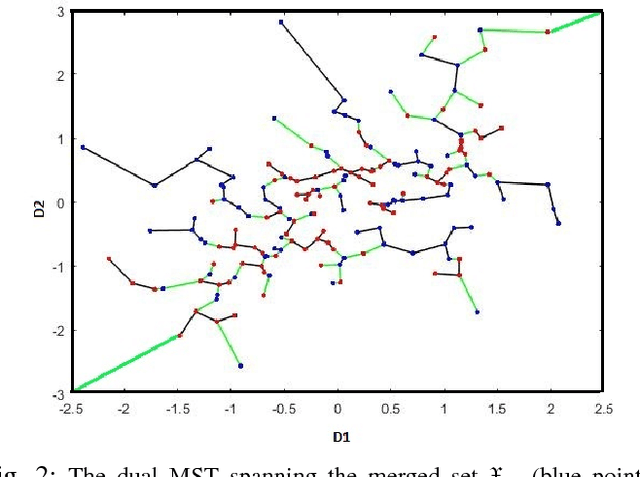
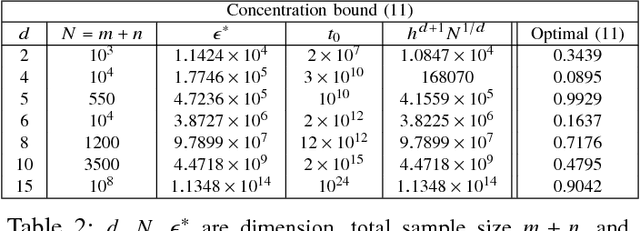
Bounding the best achievable error probability for binary classification problems is relevant to many applications including machine learning, signal processing, and information theory. Many bounds on the Bayes binary classification error rate depend on information divergences between the pair of class distributions. Recently, the Henze-Penrose (HP) divergence has been proposed for bounding classification error probability. We consider the problem of empirically estimating the HP-divergence from random samples. We derive a bound on the convergence rate for the Friedman-Rafsky (FR) estimator of the HP-divergence, which is related to a multivariate runs statistic for testing between two distributions. The FR estimator is derived from a multicolored Euclidean minimal spanning tree (MST) that spans the merged samples. We obtain a concentration inequality for the Friedman-Rafsky estimator of the Henze-Penrose divergence. We validate our results experimentally and illustrate their application to real datasets.

Scalable Mutual Information Estimation using Dependence Graphs

We propose a unified method for empirical non-parametric estimation of general Mutual Information (MI) function between the random vectors in $\mathbb{R}^d$ based on $N$ i.i.d. samples. The proposed low complexity estimator is based on a bipartite graph, referred to as dependence graph. The data points are mapped to the vertices of this graph using randomized Locality Sensitive Hashing (LSH). The vertex and edge weights are defined in terms of marginal and joint hash collisions. For a given set of hash parameters $\epsilon(1), \ldots, \epsilon(k)$, a base estimator is defined as a weighted average of the transformed edge weights. The proposed estimator, called the ensemble dependency graph estimator (EDGE), is obtained as a weighted average of the base estimators, where the weights are computed offline as the solution of a linear programming problem. EDGE achieves optimal computational complexity $O(N)$, and can achieve the optimal parametric MSE rate of $O(1/N)$ if the density is $d$ times differentiable. To the best of our knowledge EDGE is the first non-parametric MI estimator that can achieve parametric MSE rates with linear time complexity.

Direct Estimation of Information Divergence Using Nearest Neighbor Ratios

We propose a direct estimation method for R\'{e}nyi and f-divergence measures based on a new graph theoretical interpretation. Suppose that we are given two sample sets $X$ and $Y$, respectively with $N$ and $M$ samples, where $\eta:=M/N$ is a constant value. Considering the $k$-nearest neighbor ($k$-NN) graph of $Y$ in the joint data set $(X,Y)$, we show that the average powered ratio of the number of $X$ points to the number of $Y$ points among all $k$-NN points is proportional to R\'{e}nyi divergence of $X$ and $Y$ densities. A similar method can also be used to estimate f-divergence measures. We derive bias and variance rates, and show that for the class of $\gamma$-H\"{o}lder smooth functions, the estimator achieves the MSE rate of $O(N^{-2\gamma/(\gamma+d)})$. Furthermore, by using a weighted ensemble estimation technique, for density functions with continuous and bounded derivatives of up to the order $d$, and some extra conditions at the support set boundary, we derive an ensemble estimator that achieves the parametric MSE rate of $O(1/N)$. Our estimators are more computationally tractable than other competing estimators, which makes them appealing in many practical applications.

Information Theoretic Structure Learning with Confidence

Information theoretic measures (e.g. the Kullback Liebler divergence and Shannon mutual information) have been used for exploring possibly nonlinear multivariate dependencies in high dimension. If these dependencies are assumed to follow a Markov factor graph model, this exploration process is called structure discovery. For discrete-valued samples, estimates of the information divergence over the parametric class of multinomial models lead to structure discovery methods whose mean squared error achieves parametric convergence rates as the sample size grows. However, a naive application of this method to continuous nonparametric multivariate models converges much more slowly. In this paper we introduce a new method for nonparametric structure discovery that uses weighted ensemble divergence estimators that achieve parametric convergence rates and obey an asymptotic central limit theorem that facilitates hypothesis testing and other types of statistical validation.

Low-Complexity Stochastic Generalized Belief Propagation

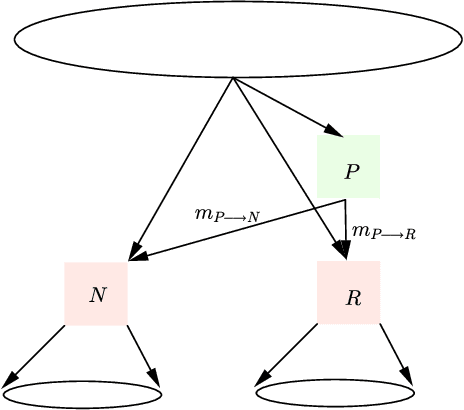
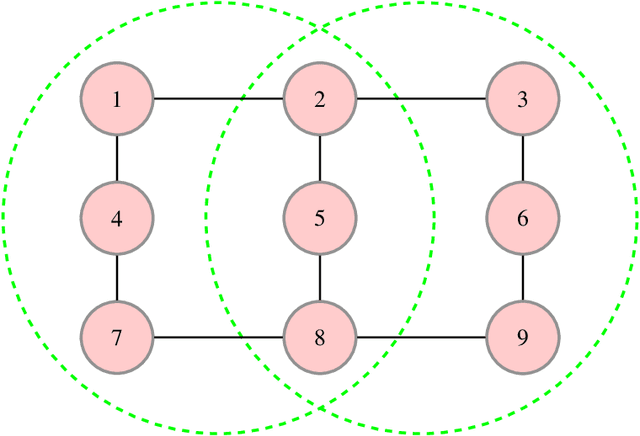
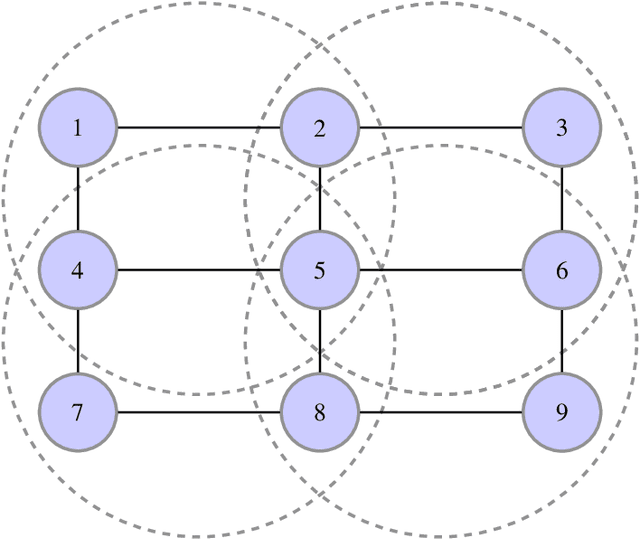
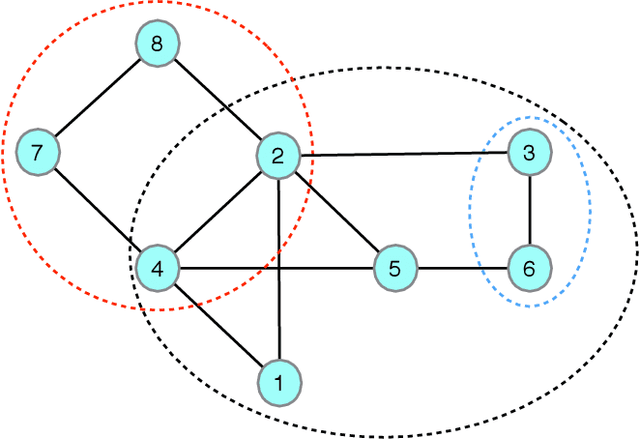
The generalized belief propagation (GBP), introduced by Yedidia et al., is an extension of the belief propagation (BP) algorithm, which is widely used in different problems involved in calculating exact or approximate marginals of probability distributions. In many problems, it has been observed that the accuracy of GBP considerably outperforms that of BP. However, because in general the computational complexity of GBP is higher than BP, its application is limited in practice. In this paper, we introduce a stochastic version of GBP called stochastic generalized belief propagation (SGBP) that can be considered as an extension to the stochastic BP (SBP) algorithm introduced by Noorshams et al. They have shown that SBP reduces the complexity per iteration of BP by an order of magnitude in alphabet size. In contrast to SBP, SGBP can reduce the computation complexity if certain topological conditions are met by the region graph associated to a graphical model. However, this reduction can be larger than only one order of magnitude in alphabet size. In this paper, we characterize these conditions and the amount of computation gain that we can obtain by using SGBP. Finally, using similar proof techniques employed by Noorshams et al., for general graphical models satisfy contraction conditions, we prove the asymptotic convergence of SGBP to the unique GBP fixed point, as well as providing non-asymptotic upper bounds on the mean square error and on the high probability error.