Coding for Computation: Efficient Compression of Neural Networks for Reconfigurable Hardware

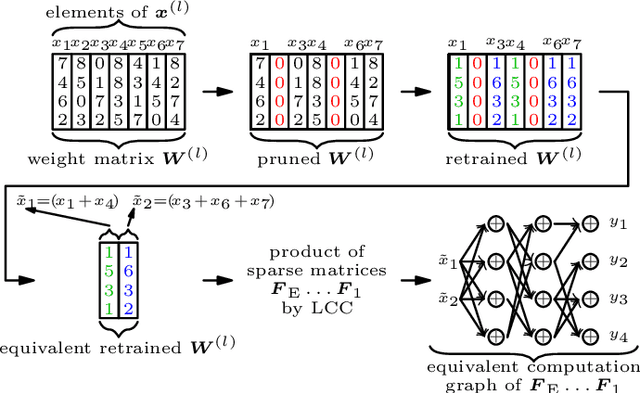
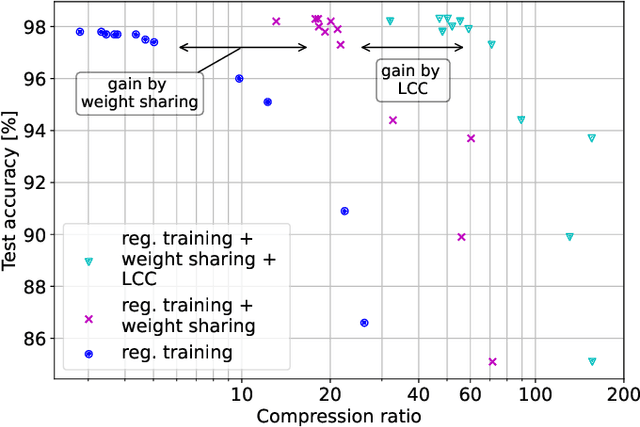
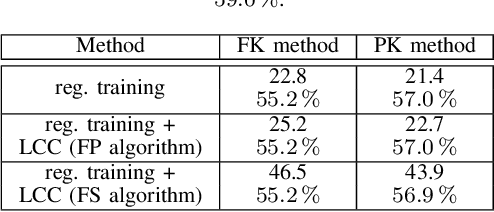
As state of the art neural networks (NNs) continue to grow in size, their resource-efficient implementation becomes ever more important. In this paper, we introduce a compression scheme that reduces the number of computations required for NN inference on reconfigurable hardware such as FPGAs. This is achieved by combining pruning via regularized training, weight sharing and linear computation coding (LCC). Contrary to common NN compression techniques, where the objective is to reduce the memory used for storing the weights of the NNs, our approach is optimized to reduce the number of additions required for inference in a hardware-friendly manner. The proposed scheme achieves competitive performance for simple multilayer perceptrons, as well as for large scale deep NNs such as ResNet-34.

MIMO-PASS: Uplink and Downlink Transmission via MIMO Pinching-Antenna Systems

Pinching-antenna systems (PASSs) are a recent flexible-antenna technology that is realized by attaching simple components, referred to as pinching elements, to dielectric waveguides. This work explores the potential of deploying PASS for uplink and downlink transmission in multiuser MIMO settings. For downlink PASS-aided communication, we formulate the optimal hybrid beamforming, in which the digital precoding matrix at the access point and the location of pinching elements on the waveguides are jointly optimized to maximize the achievable weighted sum-rate. Invoking fractional programming and Gauss-Seidel approach, we propose two low-complexity algorithms to iteratively update the precoding matrix and activated locations of the pinching elements. We further study uplink transmission aided by a PASS, where an iterative scheme is designed to address the underlying hybrid multiuser detection problem. We validate the proposed schemes through extensive numerical experiments. The results demonstrate that using a PASS, the throughput in both uplink and downlink is boosted significantly as compared with baseline MIMO architectures, such as massive MIMO~and classical hybrid analog-digital designs. This highlights the great potential of PASSs, making it a promising reconfigurable antenna technology for next-generation wireless systems.

Downlink Beamforming with Pinching-Antenna Assisted MIMO Systems

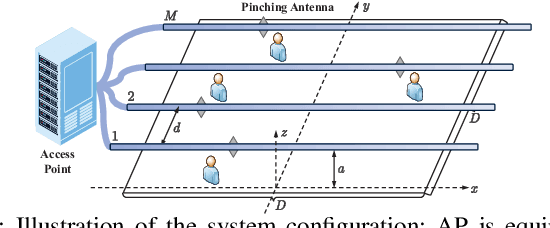
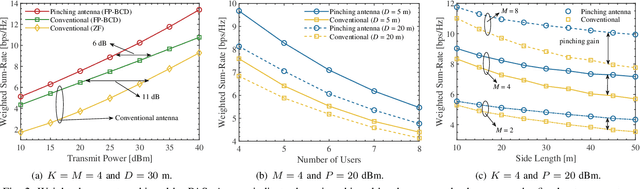
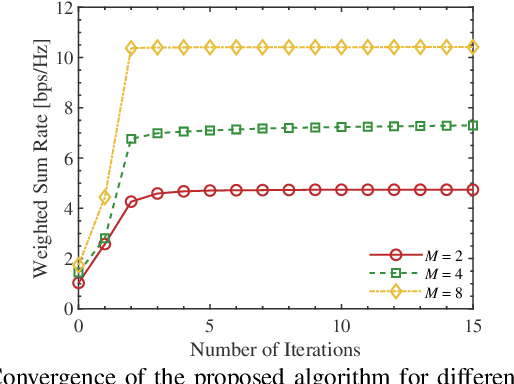
Pinching antennas have been recently proposed as a promising flexible-antenna technology, which can be implemented by attaching low-cost pinching elements to dielectric waveguides. This work explores the potential of employing pinching antenna systems (PASs) for downlink transmission in a multiuser MIMO setting. We consider the problem of hybrid beamforming, where the digital precoder at the access point and the activated locations of the pinching elements are jointly optimized to maximize the achievable weighted sum-rate. Invoking fractional programming, a novel low-complexity algorithm is developed to iteratively update the precoding matrix and the locations of the pinching antennas. We validate the proposed scheme through extensive numerical experiments. Our investigations demonstrate that using PAS the system throughput can be significantly boosted as compared with the conventional fixed-location antenna systems, enlightening the potential of PAS as an enabling candidate for next-generation wireless networks.

Universal Training of Neural Networks to Achieve Bayes Optimal Classification Accuracy

This work invokes the notion of $f$-divergence to introduce a novel upper bound on the Bayes error rate of a general classification task. We show that the proposed bound can be computed by sampling from the output of a parameterized model. Using this practical interpretation, we introduce the Bayes optimal learning threshold (BOLT) loss whose minimization enforces a classification model to achieve the Bayes error rate. We validate the proposed loss for image and text classification tasks, considering MNIST, Fashion-MNIST, CIFAR-10, and IMDb datasets. Numerical experiments demonstrate that models trained with BOLT achieve performance on par with or exceeding that of cross-entropy, particularly on challenging datasets. This highlights the potential of BOLT in improving generalization.

Regularized Top-$k$: A Bayesian Framework for Gradient Sparsification

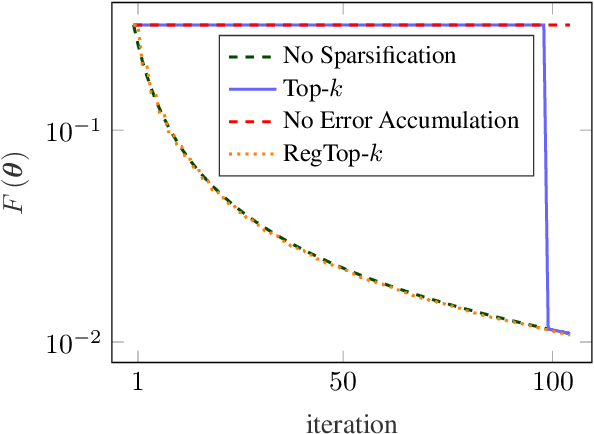
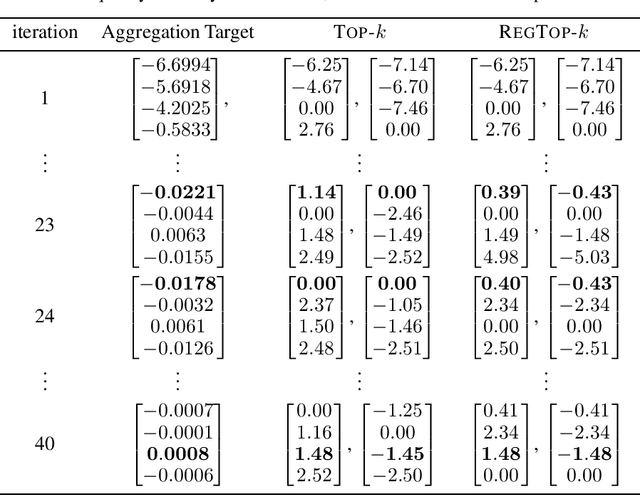
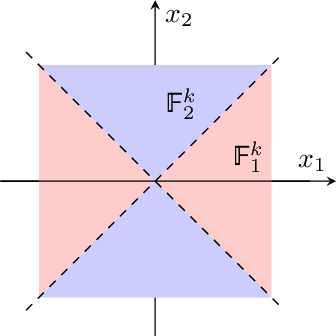
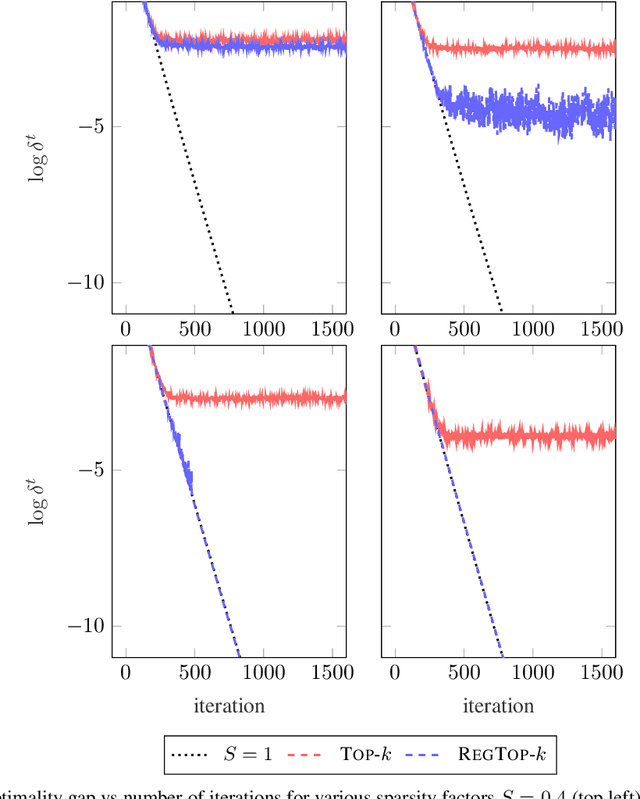
Error accumulation is effective for gradient sparsification in distributed settings: initially-unselected gradient entries are eventually selected as their accumulated error exceeds a certain level. The accumulation essentially behaves as a scaling of the learning rate for the selected entries. Although this property prevents the slow-down of lateral movements in distributed gradient descent, it can deteriorate convergence in some settings. This work proposes a novel sparsification scheme that controls the learning rate scaling of error accumulation. The development of this scheme follows two major steps: first, gradient sparsification is formulated as an inverse probability (inference) problem, and the Bayesian optimal sparsification mask is derived as a maximum-a-posteriori estimator. Using the prior distribution inherited from Top-$k$, we derive a new sparsification algorithm which can be interpreted as a regularized form of Top-$k$. We call this algorithm regularized Top-$k$ (RegTop-$k$). It utilizes past aggregated gradients to evaluate posterior statistics of the next aggregation. It then prioritizes the local accumulated gradient entries based on these posterior statistics. We validate our derivation through numerical experiments. In distributed linear regression, it is observed that while Top-$k$ remains at a fixed distance from the global optimum, RegTop-$k$ converges to the global optimum at significantly higher compression ratios. We further demonstrate the generalization of this observation by employing RegTop-$k$ in distributed training of ResNet-18 on CIFAR-10, where it noticeably outperforms Top-$k$.

Over-the-Air Fair Federated Learning via Multi-Objective Optimization

In federated learning (FL), heterogeneity among the local dataset distributions of clients can result in unsatisfactory performance for some, leading to an unfair model. To address this challenge, we propose an over-the-air fair federated learning algorithm (OTA-FFL), which leverages over-the-air computation to train fair FL models. By formulating FL as a multi-objective minimization problem, we introduce a modified Chebyshev approach to compute adaptive weighting coefficients for gradient aggregation in each communication round. To enable efficient aggregation over the multiple access channel, we derive analytical solutions for the optimal transmit scalars at the clients and the de-noising scalar at the parameter server. Extensive experiments demonstrate the superiority of OTA-FFL in achieving fairness and robust performance compared to existing methods.

GP-FL: Model-Based Hessian Estimation for Second-Order Over-the-Air Federated Learning

Second-order methods are widely adopted to improve the convergence rate of learning algorithms. In federated learning (FL), these methods require the clients to share their local Hessian matrices with the parameter server (PS), which comes at a prohibitive communication cost. A classical solution to this issue is to approximate the global Hessian matrix from the first-order information. Unlike in idealized networks, this solution does not perform effectively in over-the-air FL settings, where the PS receives noisy versions of the local gradients. This paper introduces a novel second-order FL framework tailored for wireless channels. The pivotal innovation lies in the PS's capability to directly estimate the global Hessian matrix from the received noisy local gradients via a non-parametric method: the PS models the unknown Hessian matrix as a Gaussian process, and then uses the temporal relation between the gradients and Hessian along with the channel model to find a stochastic estimator for the global Hessian matrix. We refer to this method as Gaussian process-based Hessian modeling for wireless FL (GP-FL) and show that it exhibits a linear-quadratic convergence rate. Numerical experiments on various datasets demonstrate that GP-FL outperforms all classical baseline first and second order FL approaches.

Rate-Constrained Quantization for Communication-Efficient Federated Learning

Quantization is a common approach to mitigate the communication cost of federated learning (FL). In practice, the quantized local parameters are further encoded via an entropy coding technique, such as Huffman coding, for efficient data compression. In this case, the exact communication overhead is determined by the bit rate of the encoded gradients. Recognizing this fact, this work deviates from the existing approaches in the literature and develops a novel quantized FL framework, called \textbf{r}ate-\textbf{c}onstrained \textbf{fed}erated learning (RC-FED), in which the gradients are quantized subject to both fidelity and data rate constraints. We formulate this scheme, as a joint optimization in which the quantization distortion is minimized while the rate of encoded gradients is kept below a target threshold. This enables for a tunable trade-off between quantization distortion and communication cost. We analyze the convergence behavior of RC-FED, and show its superior performance against baseline quantized FL schemes on several datasets.

Graph-based Algorithms for Linear Computation Coding

We revisit existing linear computation coding (LCC) algorithms, and introduce a new framework that measures the computational cost of computing multidimensional linear functions, not only in terms of the number of additions, but also with respect to their suitability for parallel processing. Utilizing directed acyclic graphs, which correspond to signal flow graphs in hardware, we propose a novel LCC algorithm that controls the trade-off between the total number of operations and their parallel executability. Numerical evaluations show that the proposed algorithm, constrained to a fully parallel structure, outperforms existing schemes.

Linear Computation Coding: Exponential Search and Reduced-State Algorithms

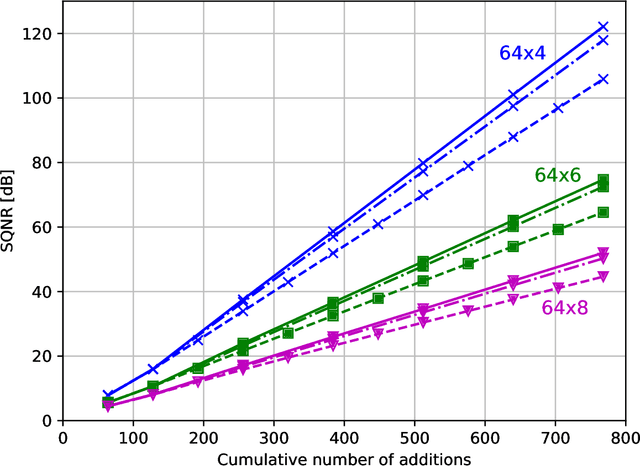
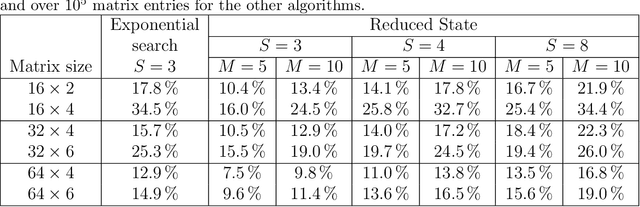
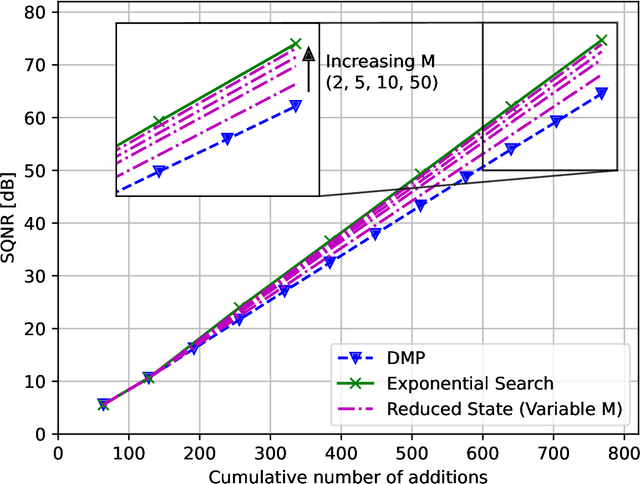
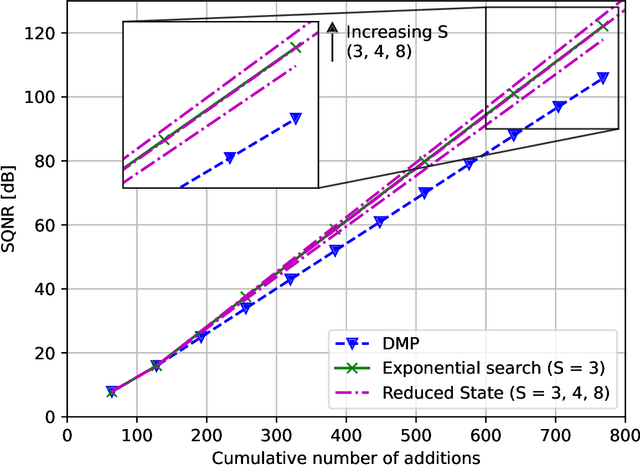
Linear computation coding is concerned with the compression of multidimensional linear functions, i.e. with reducing the computational effort of multiplying an arbitrary vector to an arbitrary, but known, constant matrix. This paper advances over the state-of-the art, that is based on a discrete matching pursuit (DMP) algorithm, by a step-wise optimal search. Offering significant performance gains over DMP, it is however computationally infeasible for large matrices and high accuracy. Therefore, a reduced-state algorithm is introduced that offers performance superior to DMP, while still being computationally feasible even for large matrices. Depending on the matrix size, the performance gain over DMP is on the order of at least 10%.