Low-Complexity Stochastic Generalized Belief Propagation
Paper and Code
May 06, 2016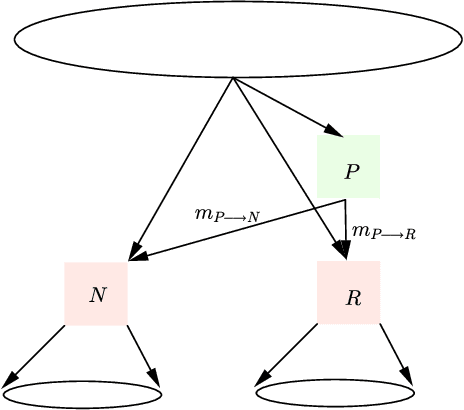
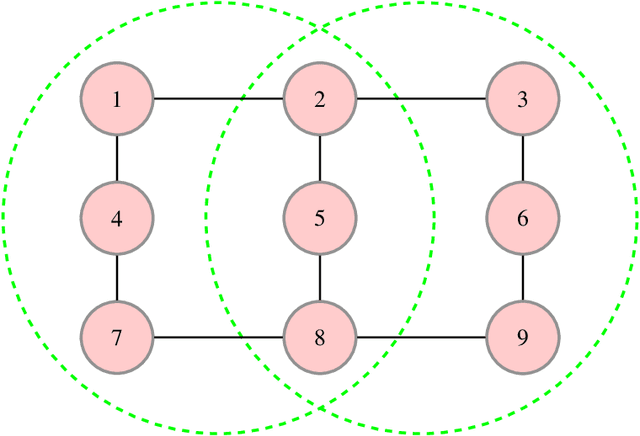
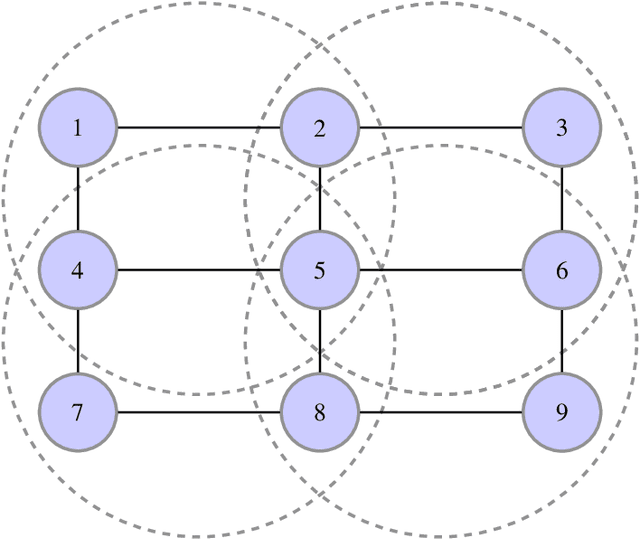
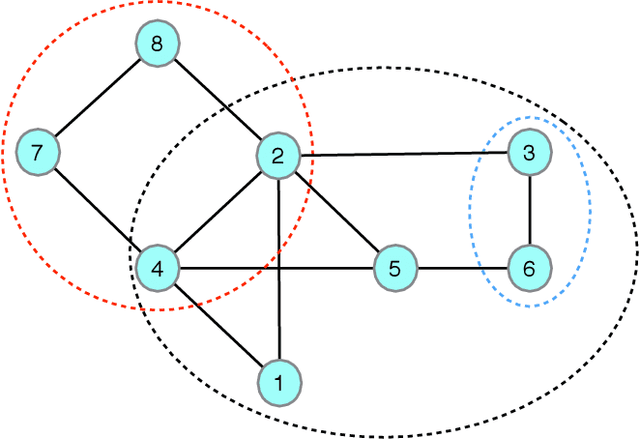
The generalized belief propagation (GBP), introduced by Yedidia et al., is an extension of the belief propagation (BP) algorithm, which is widely used in different problems involved in calculating exact or approximate marginals of probability distributions. In many problems, it has been observed that the accuracy of GBP considerably outperforms that of BP. However, because in general the computational complexity of GBP is higher than BP, its application is limited in practice. In this paper, we introduce a stochastic version of GBP called stochastic generalized belief propagation (SGBP) that can be considered as an extension to the stochastic BP (SBP) algorithm introduced by Noorshams et al. They have shown that SBP reduces the complexity per iteration of BP by an order of magnitude in alphabet size. In contrast to SBP, SGBP can reduce the computation complexity if certain topological conditions are met by the region graph associated to a graphical model. However, this reduction can be larger than only one order of magnitude in alphabet size. In this paper, we characterize these conditions and the amount of computation gain that we can obtain by using SGBP. Finally, using similar proof techniques employed by Noorshams et al., for general graphical models satisfy contraction conditions, we prove the asymptotic convergence of SGBP to the unique GBP fixed point, as well as providing non-asymptotic upper bounds on the mean square error and on the high probability error.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge