Large and Small Deviations for Statistical Sequence Matching

We revisit the problem of statistical sequence matching between two databases of sequences initiated by Unnikrishnan (TIT 2015) and derive theoretical performance guarantees for the generalized likelihood ratio test (GLRT). We first consider the case where the number of matched pairs of sequences between the databases is known. In this case, the task is to accurately find the matched pairs of sequences among all possible matches between the sequences in the two databases. We analyze the performance of the GLRT by Unnikrishnan and explicitly characterize the tradeoff between the mismatch and false reject probabilities under each hypothesis in both large and small deviations regimes. Furthermore, we demonstrate the optimality of Unnikrishnan's GLRT test under the generalized Neyman-Person criterion for both regimes and illustrate our theoretical results via numerical examples. Subsequently, we generalize our achievability analyses to the case where the number of matched pairs is unknown, and an additional error probability needs to be considered. When one of the two databases contains a single sequence, the problem of statistical sequence matching specializes to the problem of multiple classification introduced by Gutman (TIT 1989). For this special case, our result for the small deviations regime strengthens previous result of Zhou, Tan and Motani (Information and Inference 2020) by removing unnecessary conditions on the generating distributions.

Fair Structure Learning in Heterogeneous Graphical Models

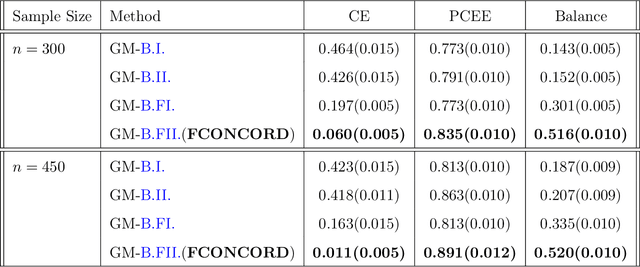
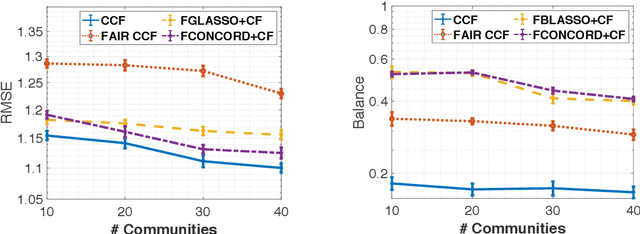
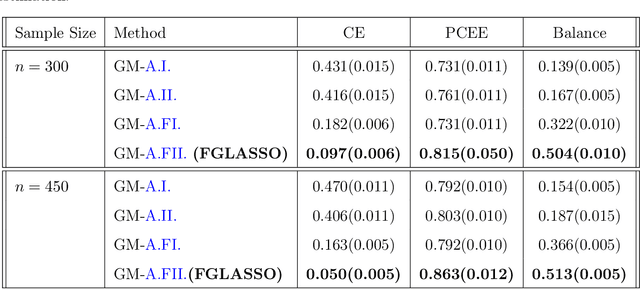
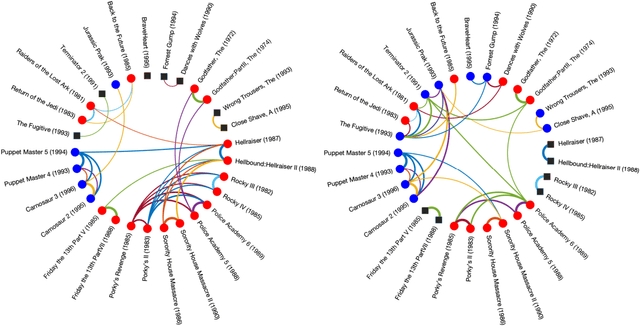
Inference of community structure in probabilistic graphical models may not be consistent with fairness constraints when nodes have demographic attributes. Certain demographics may be over-represented in some detected communities and under-represented in others. This paper defines a novel $\ell_1$-regularized pseudo-likelihood approach for fair graphical model selection. In particular, we assume there is some community or clustering structure in the true underlying graph, and we seek to learn a sparse undirected graph and its communities from the data such that demographic groups are fairly represented within the communities. Our optimization approach uses the demographic parity definition of fairness, but the framework is easily extended to other definitions of fairness. We establish statistical consistency of the proposed method for both a Gaussian graphical model and an Ising model for, respectively, continuous and binary data, proving that our method can recover the graphs and their fair communities with high probability.

Multimodal Data Fusion in High-Dimensional Heterogeneous Datasets via Generative Models

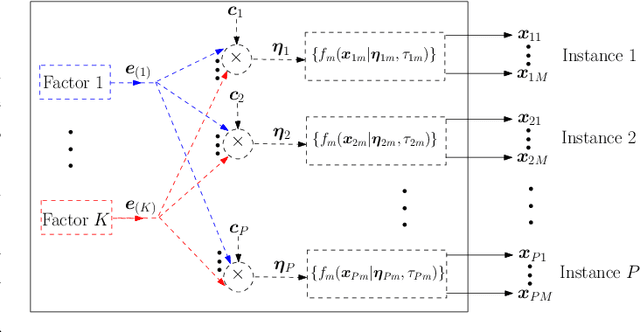
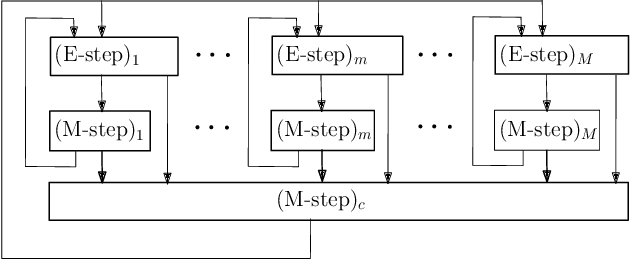
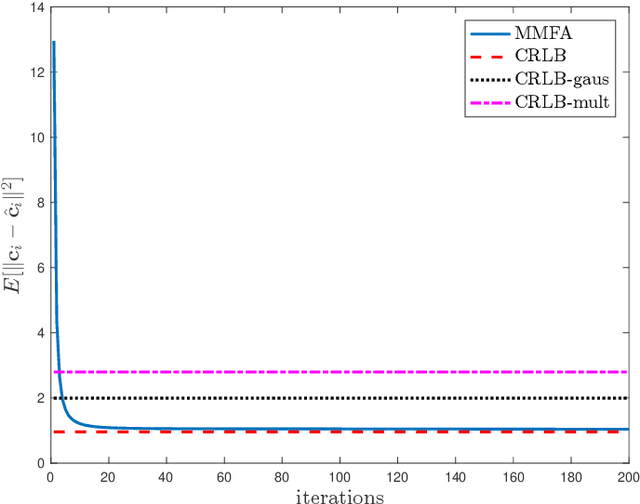
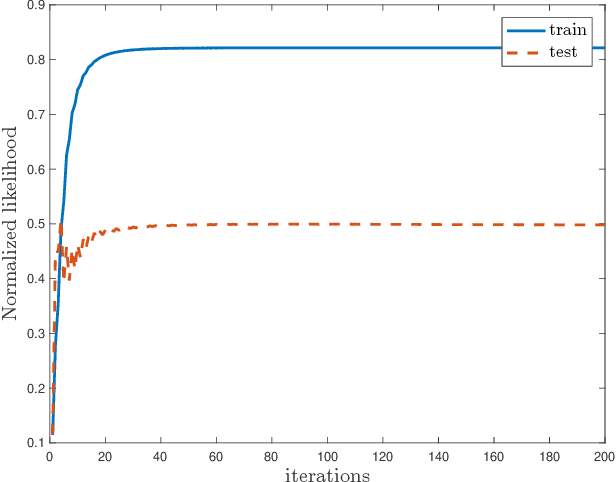
The commonly used latent space embedding techniques, such as Principal Component Analysis, Factor Analysis, and manifold learning techniques, are typically used for learning effective representations of homogeneous data. However, they do not readily extend to heterogeneous data that are a combination of numerical and categorical variables, e.g., arising from linked GPS and text data. In this paper, we are interested in learning probabilistic generative models from high-dimensional heterogeneous data in an unsupervised fashion. The learned generative model provides latent unified representations that capture the factors common to the multiple dimensions of the data, and thus enable fusing multimodal data for various machine learning tasks. Following a Bayesian approach, we propose a general framework that combines disparate data types through the natural parameterization of the exponential family of distributions. To scale the model inference to millions of instances with thousands of features, we use the Laplace-Bernstein approximation for posterior computations involving nonlinear link functions. The proposed algorithm is presented in detail for the commonly encountered heterogeneous datasets with real-valued (Gaussian) and categorical (multinomial) features. Experiments on two high-dimensional and heterogeneous datasets (NYC Taxi and MovieLens-10M) demonstrate the scalability and competitive performance of the proposed algorithm on different machine learning tasks such as anomaly detection, data imputation, and recommender systems.

OrthoReg: Robust Network Pruning Using Orthonormality Regularization

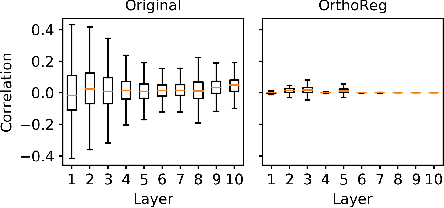
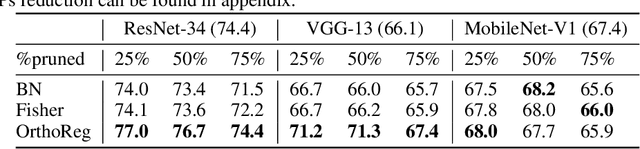
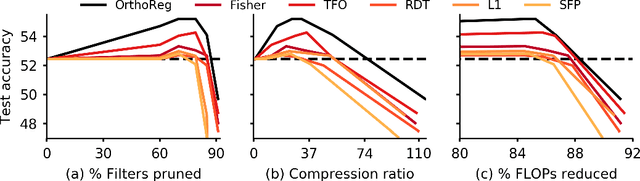
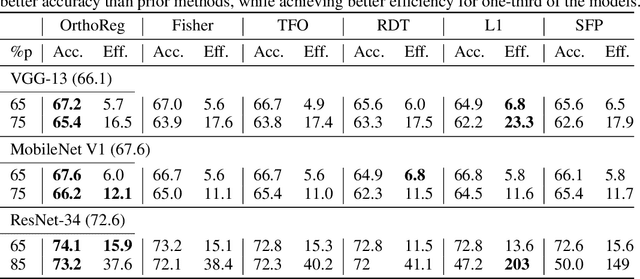
Network pruning in Convolutional Neural Networks (CNNs) has been extensively investigated in recent years. To determine the impact of pruning a group of filters on a network's accuracy, state-of-the-art pruning methods consistently assume filters of a CNN are independent. This allows the importance of a group of filters to be estimated as the sum of importances of individual filters. However, overparameterization in modern networks results in highly correlated filters that invalidate this assumption, thereby resulting in incorrect importance estimates. To address this issue, we propose OrthoReg, a principled regularization strategy that enforces orthonormality on a network's filters to reduce inter-filter correlation, thereby allowing reliable, efficient determination of group importance estimates, improved trainability of pruned networks, and efficient, simultaneous pruning of large groups of filters. When used for iterative pruning on VGG-13, MobileNet-V1, and ResNet-34, OrthoReg consistently outperforms five baseline techniques, including the state-of-the-art, on CIFAR-100 and Tiny-ImageNet. For the recently proposed Early-Bird Ticket hypothesis, which claims networks become amenable to pruning early-on in training and can be pruned after a few epochs to minimize training expenditure, we find OrthoReg significantly outperforms prior work. Code available at https://github.com/EkdeepSLubana/OrthoReg.

Geometric Online Adaptation: Graph-Based OSFS for Streaming Samples

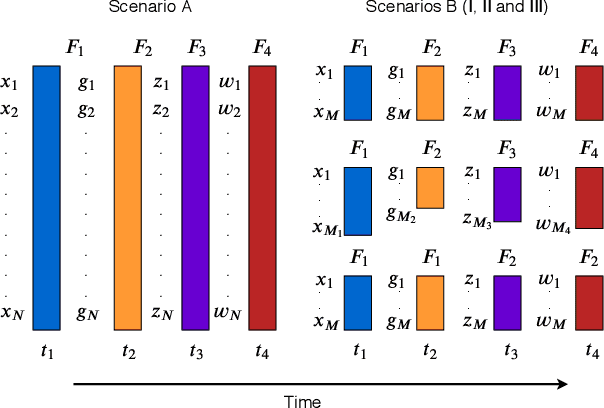
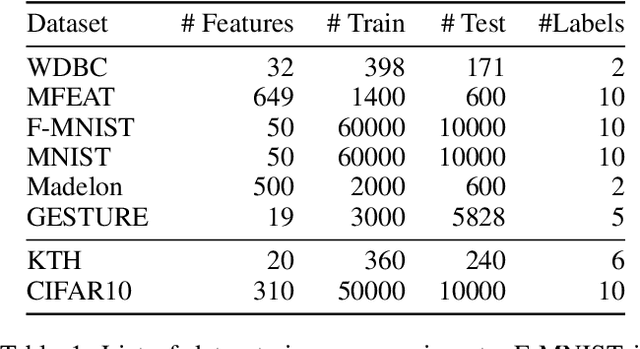
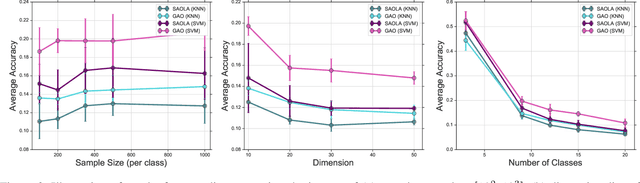
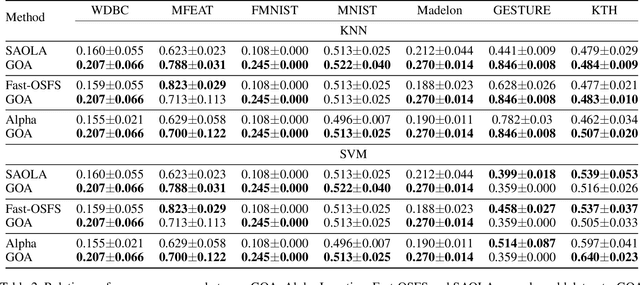
Feature selection seeks a curated subset of available features such that they contain sufficient discriminative information for a given learning task. Online streaming feature selection (OSFS) further extends this to the streaming scenario where the model gets only a single pass at features, one at a time. While this problem setting allows for training high performance models with low computational and storage requirements, this setting also makes the assumption that there is a fixed number of samples, which is often invalidated in many real-world problems. In this paper, we consider a new setting called Online Streaming Feature Selection with Streaming Samples (OSFS-SS) with a fixed class label space, where both the features and the samples are simultaneously streamed. We extend the state-of-the-art OSFS method to work in this setting. Furthermore, we introduce a novel algorithm, that has applications in both the OSFS and OSFS-SS settings, called Geometric Online Adaptation (GOA) which uses a graph-based class conditional geometric dependency (CGD) criterion to measure feature relevance and maintain a minimal feature subset with relatively high classification performance. We evaluate the proposed GOA algorithm on both simulation and real world datasets highlighting how in both the OSFS and OSFS-SS settings it achieves higher performance while maintaining smaller feature subsets than relevant baselines.

Testing that a Local Optimum of the Likelihood is Globally Optimum using Reparameterized Embeddings

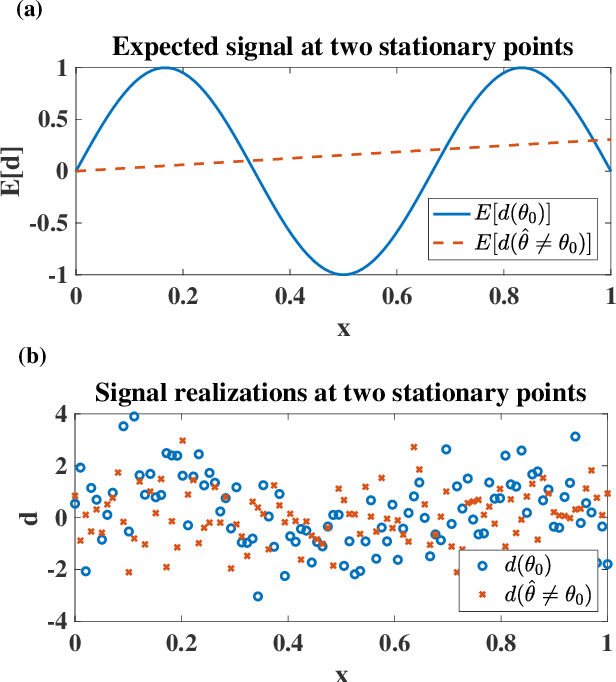
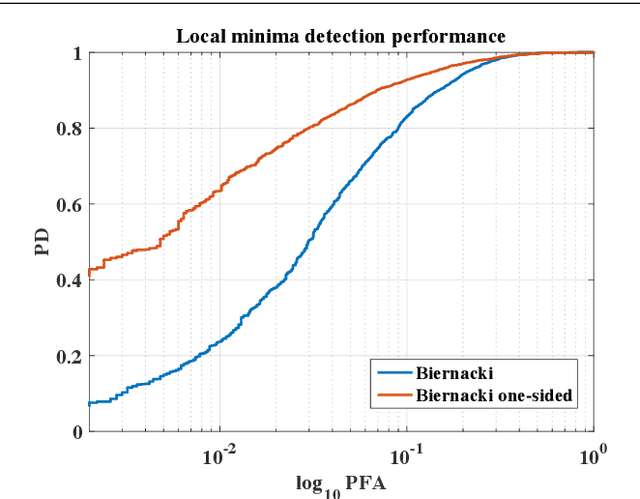
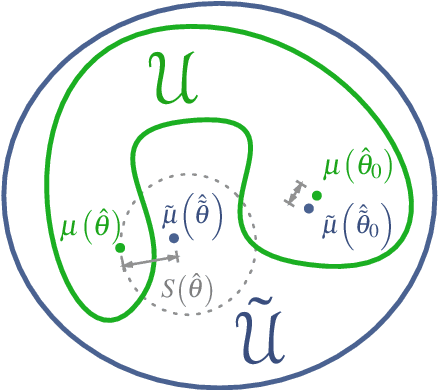
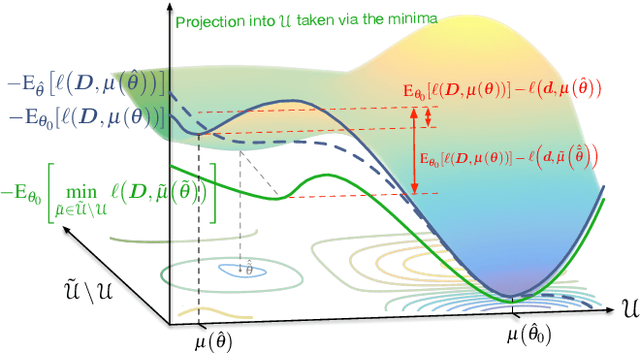
Many mathematical imaging problems are posed as non-convex optimization problems. When numerically tractable global optimization procedures are not available, one is often interested in testing ex post facto whether or not a locally convergent algorithm has found the globally optimal solution. If the problem has a statistical maximum likelihood formulation, a local test of global optimality can be constructed. In this paper, we develop an improved test, based on a global maximum validation function proposed by Biernacki, under the assumption that the statistical distribution is in the generalized location family, a condition often satisfied in imaging problems. In addition, a new reparameterization and embedding procedure is presented that exploits knowledge about the forward operator to improve the global maximum validation function. Finally, the reparameterized embedding technique is applied to a physically-motivated joint-inverse problem arising in camera blur estimation. The advantages of the proposed global optimum testing techniques are numerically demonstrated in terms of increased detection accuracy and reduced computation.

Geometric Estimation of Multivariate Dependency

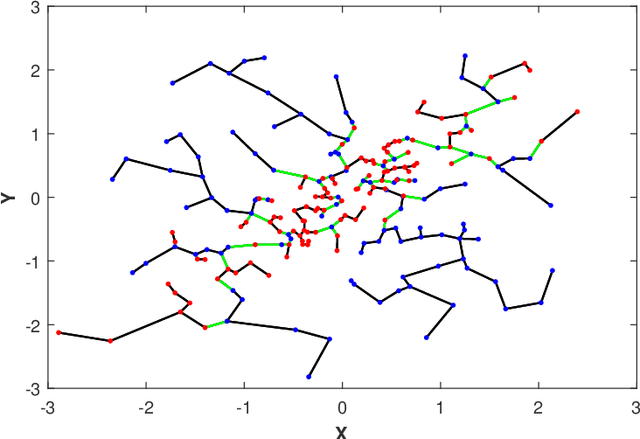
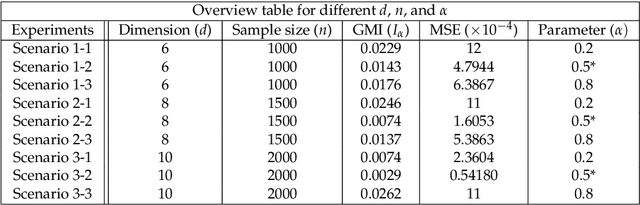
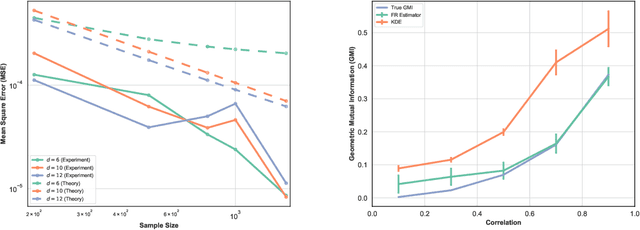
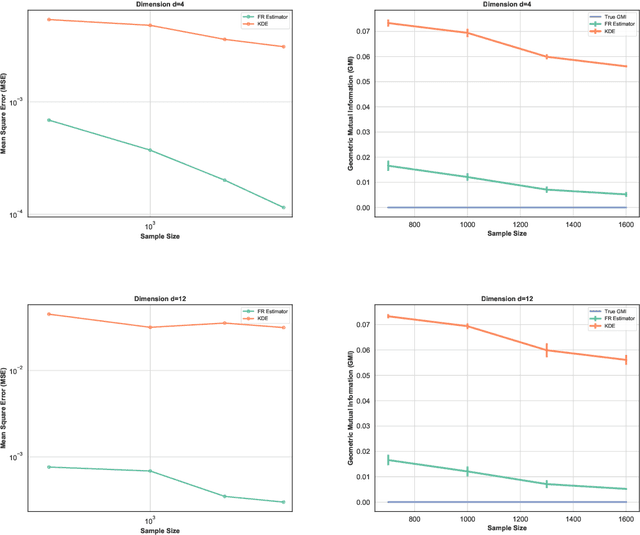
This paper proposes a geometric estimator of dependency between a pair of multivariate samples. The proposed estimator of dependency is based on a randomly permuted geometric graph (the minimal spanning tree) over the two multivariate samples. This estimator converges to a quantity that we call the geometric mutual information (GMI), which is equivalent to the Henze-Penrose divergence [1] between the joint distribution of the multivariate samples and the product of the marginals. The GMI has many of the same properties as standard MI but can be estimated from empirical data without density estimation; making it scalable to large datasets. The proposed empirical estimator of GMI is simple to implement, involving the construction of an MST spanning over both the original data and a randomly permuted version of this data. We establish asymptotic convergence of the estimator and convergence rates of the bias and variance for smooth multivariate density functions belonging to a H\"{o}lder class. We demonstrate the advantages of our proposed geometric dependency estimator in a series of experiments.

Feature Selection for multi-labeled variables via Dependency Maximization

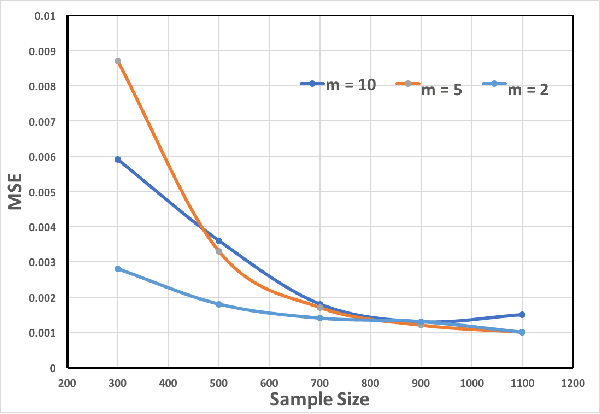
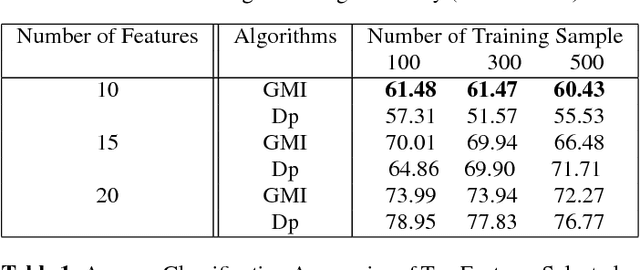
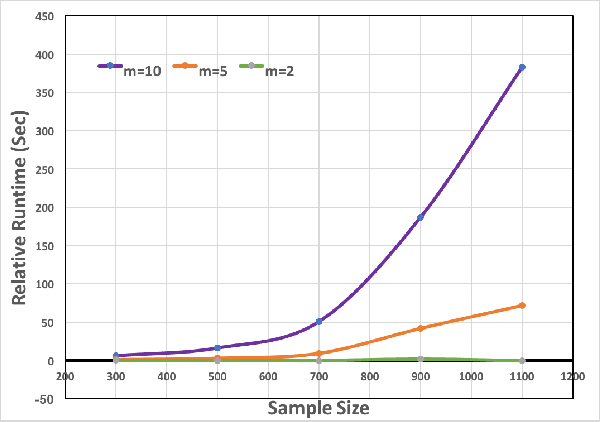
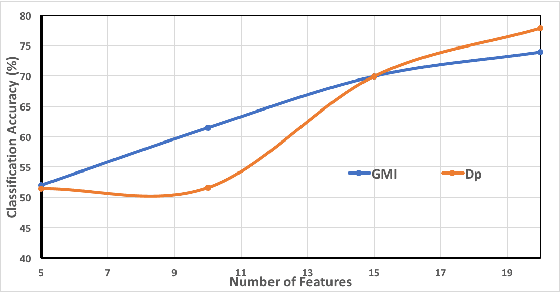
Feature selection and reducing the dimensionality of data is an essential step in data analysis. In this work, we propose a new criterion for feature selection that is formulated as conditional information between features given the labeled variable. Instead of using the standard mutual information measure based on Kullback-Leibler divergence, we use our proposed criterion to filter out redundant features for the purpose of multiclass classification. This approach results in an efficient and fast non-parametric implementation of feature selection as it can be directly estimated using a geometric measure of dependency, the global Friedman-Rafsky (FR) multivariate run test statistic constructed by a global minimal spanning tree (MST). We demonstrate the advantages of our proposed feature selection approach through simulation. In addition the proposed feature selection method is applied to the MNIST data set.

Learning to Bound the Multi-class Bayes Error

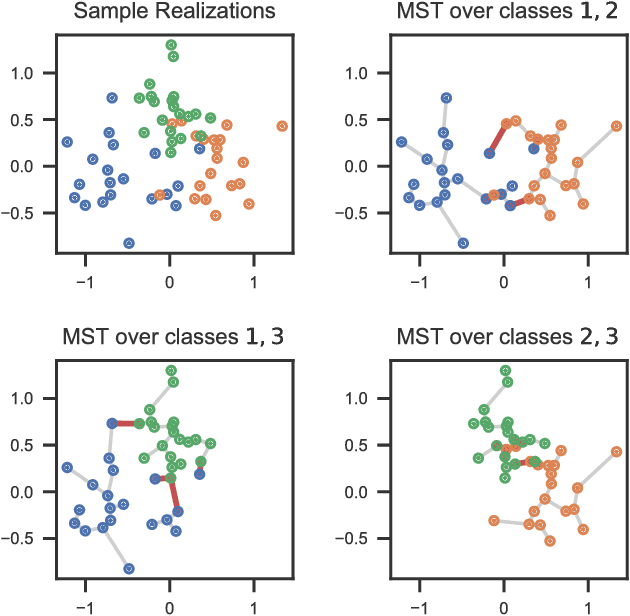
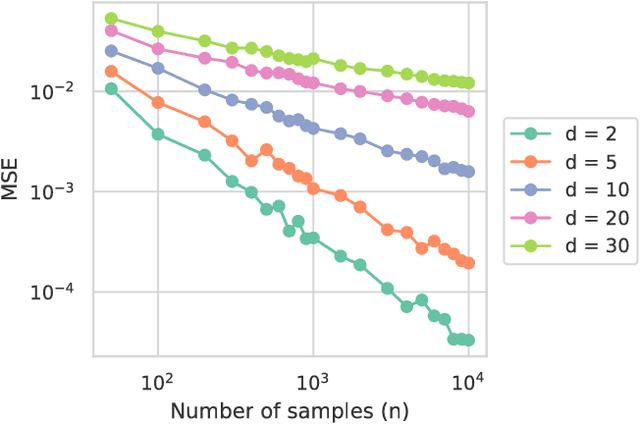
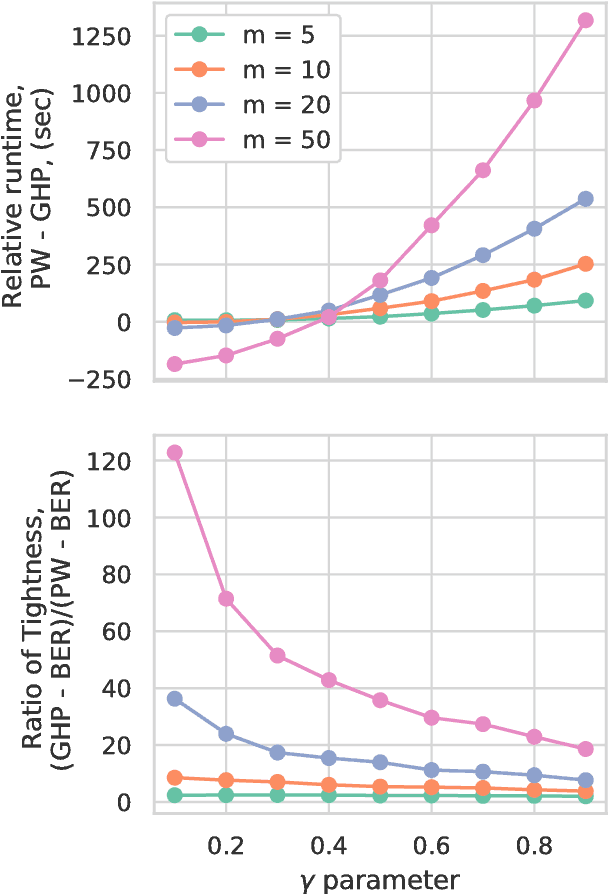
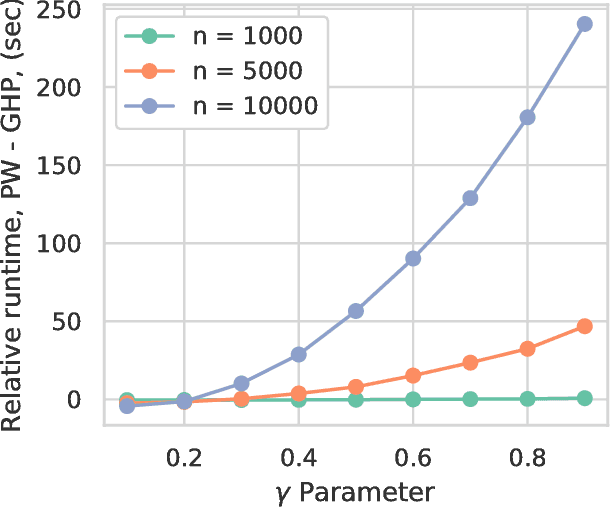
In the context of supervised learning, meta learning uses features, metadata and other information to learn about the difficulty, behavior, or composition of the problem. Using this knowledge can be useful to contextualize classifier results or allow for targeted decisions about future data sampling. In this paper, we are specifically interested in learning the Bayes error rate (BER) based on a labeled data sample. Providing a tight bound on the BER that is also feasible to estimate has been a challenge. Previous work [1] has shown that a pairwise bound based on the sum of Henze-Penrose (HP) divergence over label pairs can be directly estimated using a sum of Friedman-Rafsky (FR) multivariate run test statistics. However, in situations in which the dataset and number of classes are large, this bound is computationally infeasible to calculate and may not be tight. Other multi-class bounds also suffer from computationally complex estimation procedures. In this paper, we present a generalized HP divergence measure that allows us to estimate the Bayes error rate with log-linear computation. We prove that the proposed bound is tighter than both the pairwise method and a bound proposed by Lin [2]. We also empirically show that these bounds are close to the BER. We illustrate the proposed method on the MNIST dataset, and show its utility for the evaluation of feature reduction strategies.

Convergence Rates for Empirical Estimation of Binary Classification Bounds

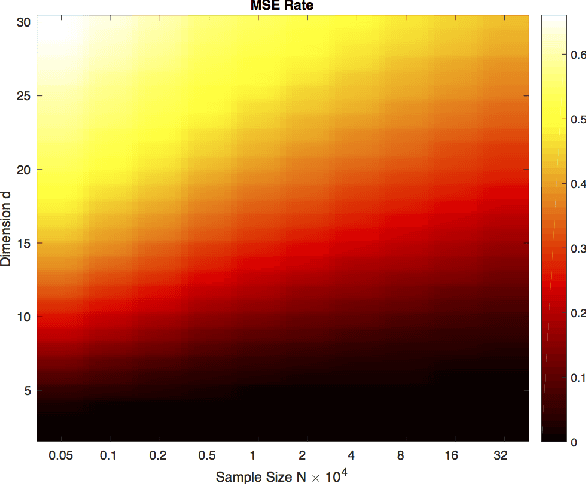
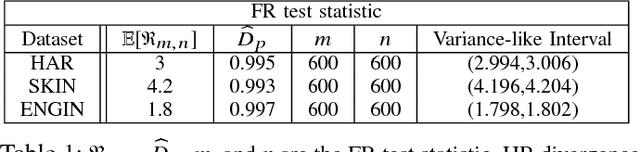
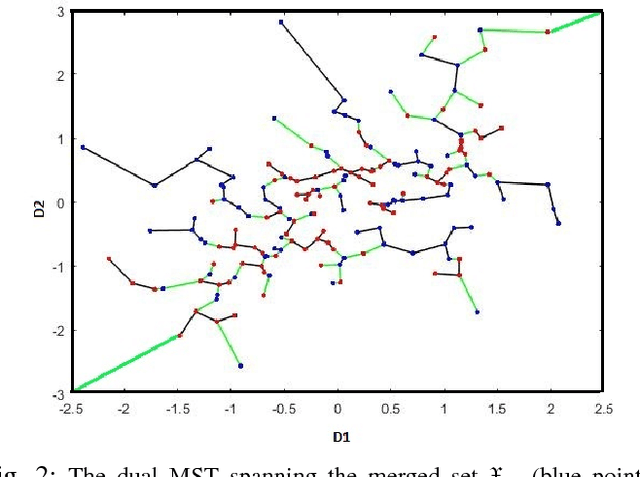
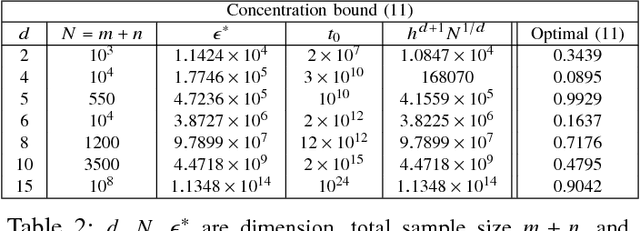
Bounding the best achievable error probability for binary classification problems is relevant to many applications including machine learning, signal processing, and information theory. Many bounds on the Bayes binary classification error rate depend on information divergences between the pair of class distributions. Recently, the Henze-Penrose (HP) divergence has been proposed for bounding classification error probability. We consider the problem of empirically estimating the HP-divergence from random samples. We derive a bound on the convergence rate for the Friedman-Rafsky (FR) estimator of the HP-divergence, which is related to a multivariate runs statistic for testing between two distributions. The FR estimator is derived from a multicolored Euclidean minimal spanning tree (MST) that spans the merged samples. We obtain a concentration inequality for the Friedman-Rafsky estimator of the Henze-Penrose divergence. We validate our results experimentally and illustrate their application to real datasets.