Brian J. Thelen
Testing that a Local Optimum of the Likelihood is Globally Optimum using Reparameterized Embeddings
May 31, 2019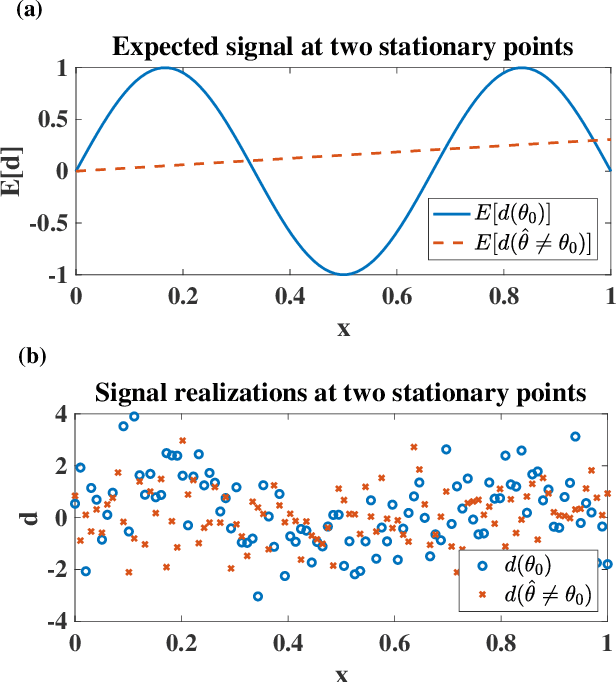
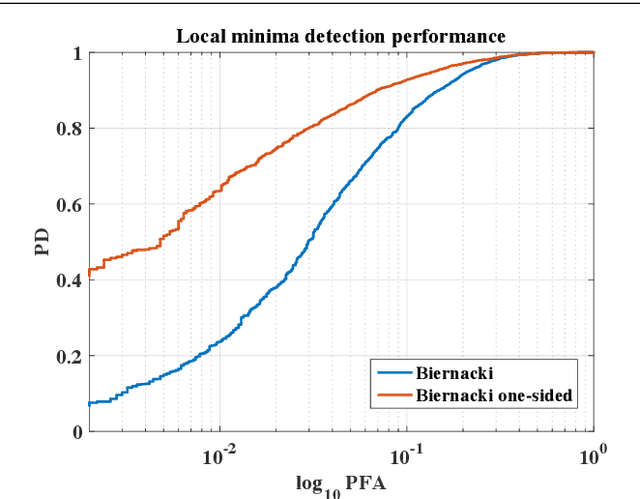
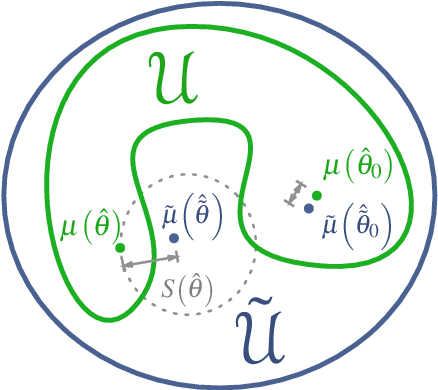
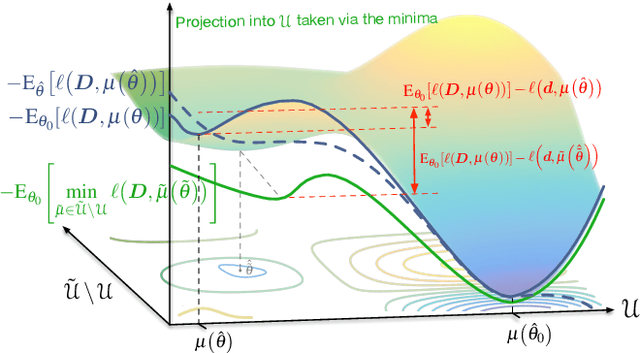
Abstract:Many mathematical imaging problems are posed as non-convex optimization problems. When numerically tractable global optimization procedures are not available, one is often interested in testing ex post facto whether or not a locally convergent algorithm has found the globally optimal solution. If the problem has a statistical maximum likelihood formulation, a local test of global optimality can be constructed. In this paper, we develop an improved test, based on a global maximum validation function proposed by Biernacki, under the assumption that the statistical distribution is in the generalized location family, a condition often satisfied in imaging problems. In addition, a new reparameterization and embedding procedure is presented that exploits knowledge about the forward operator to improve the global maximum validation function. Finally, the reparameterized embedding technique is applied to a physically-motivated joint-inverse problem arising in camera blur estimation. The advantages of the proposed global optimum testing techniques are numerically demonstrated in terms of increased detection accuracy and reduced computation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge