Incorporating Polar Field Data for Improved Solar Flare Prediction

In this paper, we consider incorporating data associated with the sun's north and south polar field strengths to improve solar flare prediction performance using machine learning models. When used to supplement local data from active regions on the photospheric magnetic field of the sun, the polar field data provides global information to the predictor. While such global features have been previously proposed for predicting the next solar cycle's intensity, in this paper we propose using them to help classify individual solar flares. We conduct experiments using HMI data employing four different machine learning algorithms that can exploit polar field information. Additionally, we propose a novel probabilistic mixture of experts model that can simply and effectively incorporate polar field data and provide on-par prediction performance with state-of-the-art solar flare prediction algorithms such as the Recurrent Neural Network (RNN). Our experimental results indicate the usefulness of the polar field data for solar flare prediction, which can improve Heidke Skill Score (HSS2) by as much as 10.1%.

A Graphical Model for Fusing Diverse Microbiome Data

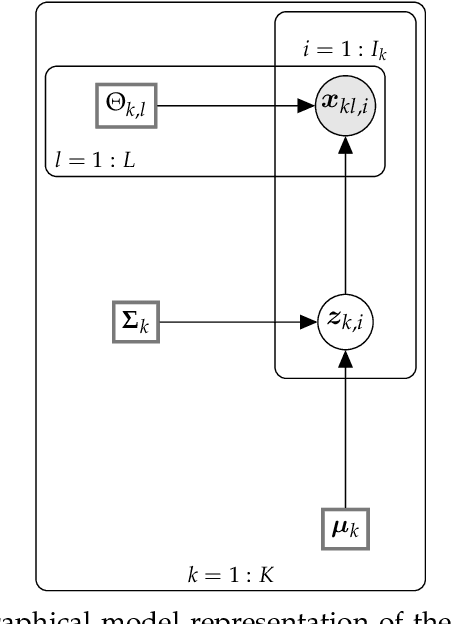
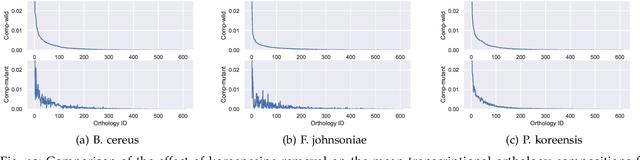
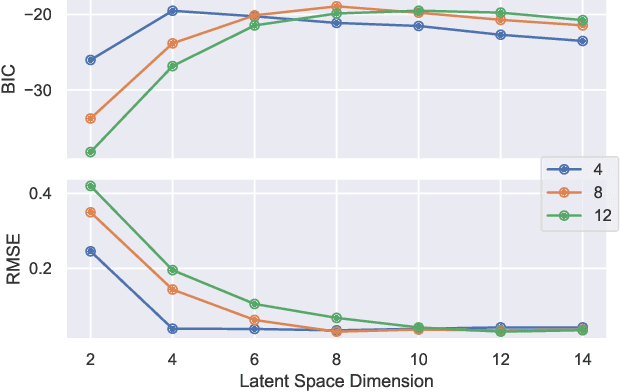
This paper develops a Bayesian graphical model for fusing disparate types of count data. The motivating application is the study of bacterial communities from diverse high dimensional features, in this case transcripts, collected from different treatments. In such datasets, there are no explicit correspondences between the communities and each correspond to different factors, making data fusion challenging. We introduce a flexible multinomial-Gaussian generative model for jointly modeling such count data. This latent variable model jointly characterizes the observed data through a common multivariate Gaussian latent space that parameterizes the set of multinomial probabilities of the transcriptome counts. The covariance matrix of the latent variables induces a covariance matrix of co-dependencies between all the transcripts, effectively fusing multiple data sources. We present a computationally scalable variational Expectation-Maximization (EM) algorithm for inferring the latent variables and the parameters of the model. The inferred latent variables provide a common dimensionality reduction for visualizing the data and the inferred parameters provide a predictive posterior distribution. In addition to simulation studies that demonstrate the variational EM procedure, we apply our model to a bacterial microbiome dataset.

Multimodal Data Fusion in High-Dimensional Heterogeneous Datasets via Generative Models

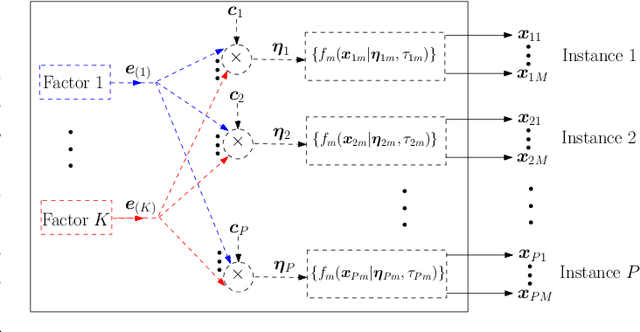
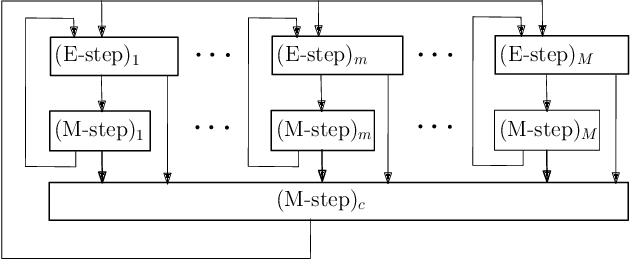
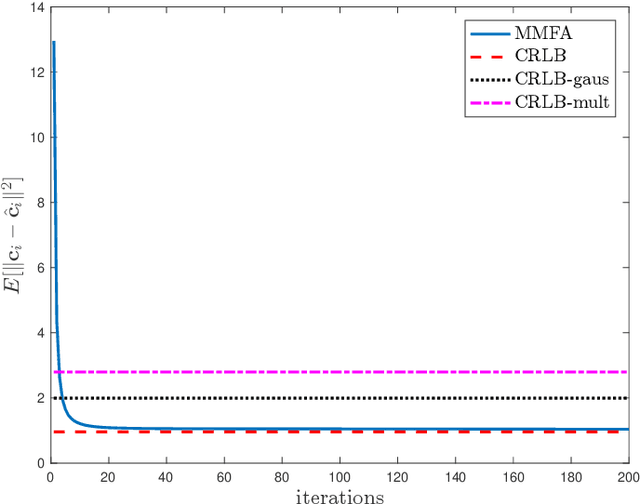
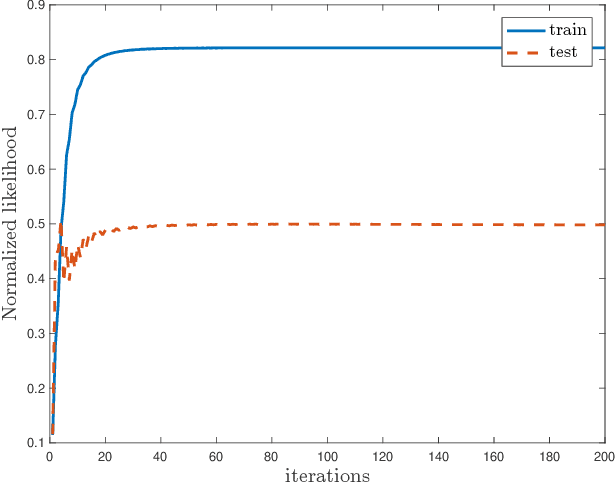
The commonly used latent space embedding techniques, such as Principal Component Analysis, Factor Analysis, and manifold learning techniques, are typically used for learning effective representations of homogeneous data. However, they do not readily extend to heterogeneous data that are a combination of numerical and categorical variables, e.g., arising from linked GPS and text data. In this paper, we are interested in learning probabilistic generative models from high-dimensional heterogeneous data in an unsupervised fashion. The learned generative model provides latent unified representations that capture the factors common to the multiple dimensions of the data, and thus enable fusing multimodal data for various machine learning tasks. Following a Bayesian approach, we propose a general framework that combines disparate data types through the natural parameterization of the exponential family of distributions. To scale the model inference to millions of instances with thousands of features, we use the Laplace-Bernstein approximation for posterior computations involving nonlinear link functions. The proposed algorithm is presented in detail for the commonly encountered heterogeneous datasets with real-valued (Gaussian) and categorical (multinomial) features. Experiments on two high-dimensional and heterogeneous datasets (NYC Taxi and MovieLens-10M) demonstrate the scalability and competitive performance of the proposed algorithm on different machine learning tasks such as anomaly detection, data imputation, and recommender systems.