A Graphical Model for Fusing Diverse Microbiome Data

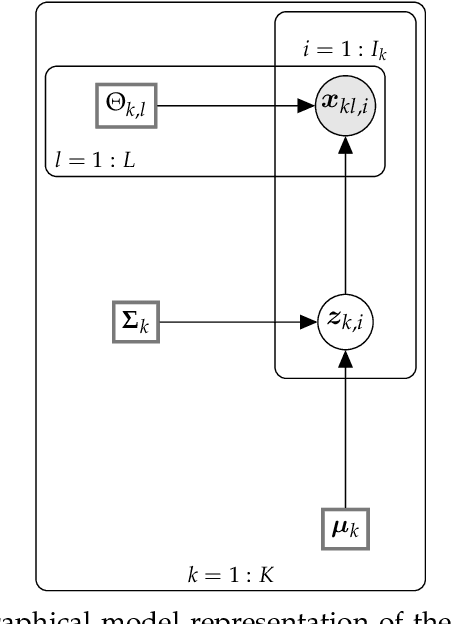
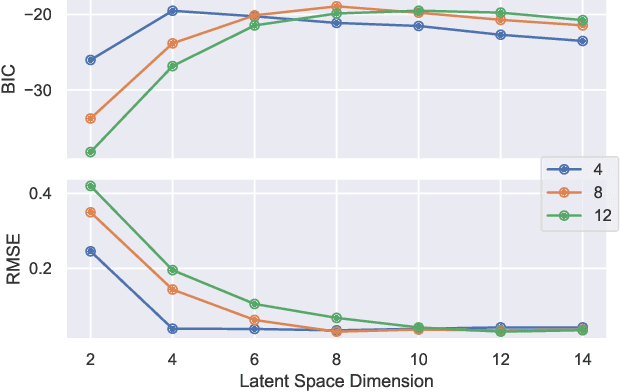
This paper develops a Bayesian graphical model for fusing disparate types of count data. The motivating application is the study of bacterial communities from diverse high dimensional features, in this case transcripts, collected from different treatments. In such datasets, there are no explicit correspondences between the communities and each correspond to different factors, making data fusion challenging. We introduce a flexible multinomial-Gaussian generative model for jointly modeling such count data. This latent variable model jointly characterizes the observed data through a common multivariate Gaussian latent space that parameterizes the set of multinomial probabilities of the transcriptome counts. The covariance matrix of the latent variables induces a covariance matrix of co-dependencies between all the transcripts, effectively fusing multiple data sources. We present a computationally scalable variational Expectation-Maximization (EM) algorithm for inferring the latent variables and the parameters of the model. The inferred latent variables provide a common dimensionality reduction for visualizing the data and the inferred parameters provide a predictive posterior distribution. In addition to simulation studies that demonstrate the variational EM procedure, we apply our model to a bacterial microbiome dataset.

High dimensional stochastic linear contextual bandit with missing covariates

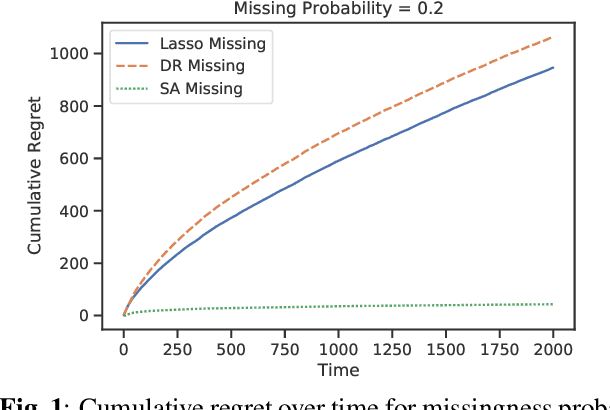
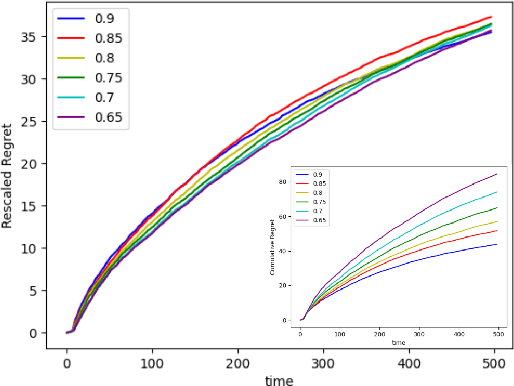
Recent works in bandit problems adopted lasso convergence theory in the sequential decision-making setting. Even with fully observed contexts, there are technical challenges that hinder the application of existing lasso convergence theory: 1) proving the restricted eigenvalue condition under conditionally sub-Gaussian noise and 2) accounting for the dependence between the context variables and the chosen actions. This paper studies the effect of missing covariates on regret for stochastic linear bandit algorithms. Our work provides a high-probability upper bound on the regret incurred by the proposed algorithm in terms of covariate sampling probabilities, showing that the regret degrades due to missingness by at most $\zeta_{min}^2$, where $\zeta_{min}$ is the minimum probability of observing covariates in the context vector. We illustrate our algorithm for the practical application of experimental design for collecting gene expression data by a sequential selection of class discriminating DNA probes.