Time-Varying Interaction Estimation Using Ensemble Methods

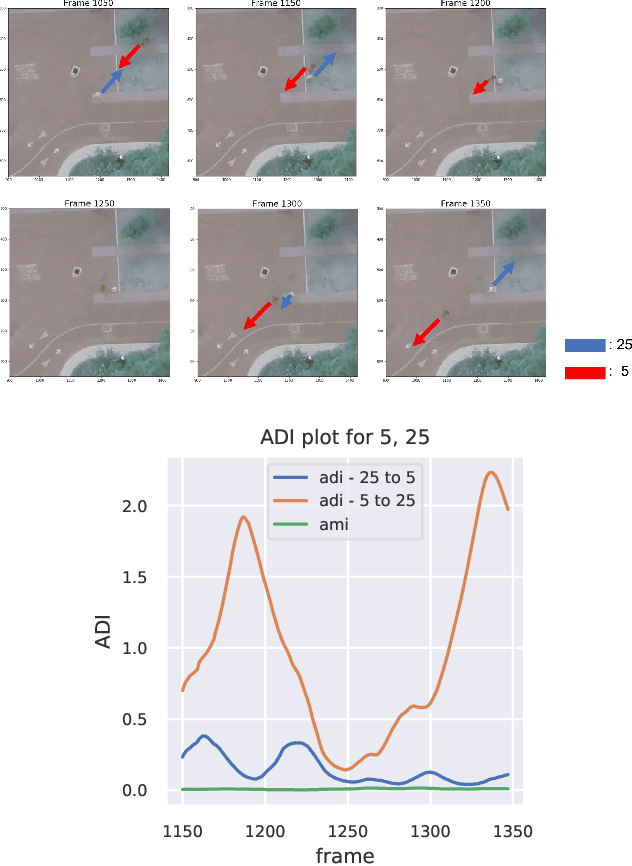
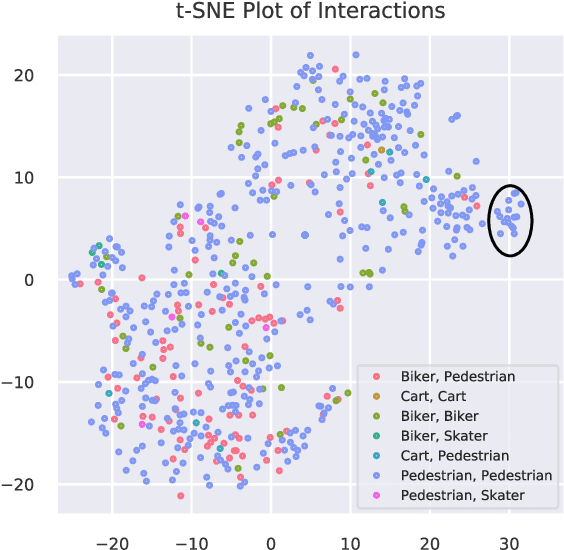
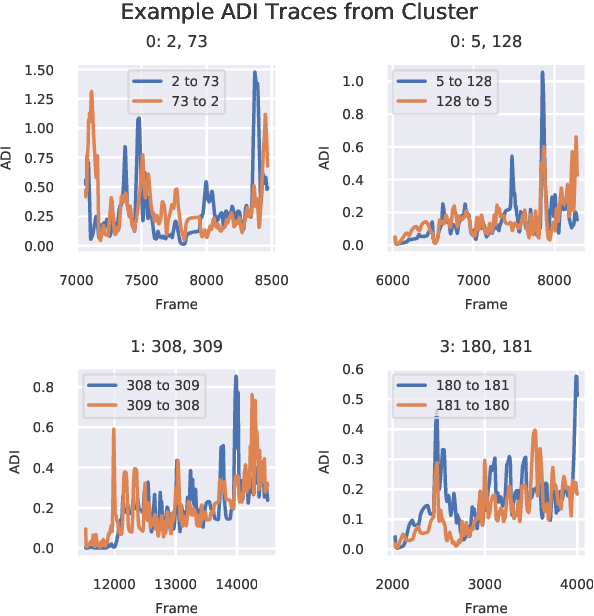
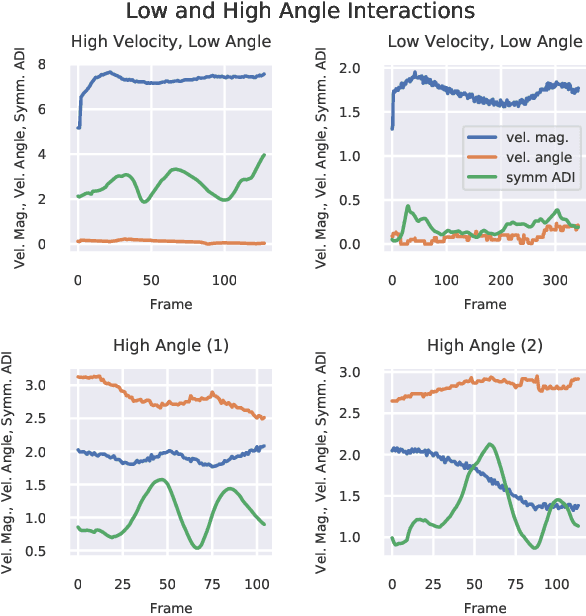
Directed information (DI) is a useful tool to explore time-directed interactions in multivariate data. However, as originally formulated DI is not well suited to interactions that change over time. In previous work, adaptive directed information was introduced to accommodate non-stationarity, while still preserving the utility of DI to discover complex dependencies between entities. There are many design decisions and parameters that are crucial to the effectiveness of ADI. Here, we apply ideas from ensemble learning in order to alleviate this issue, allowing for a more robust estimator for exploratory data analysis. We apply these techniques to interaction estimation in a crowded scene, utilizing the Stanford drone dataset as an example.

Learning to Bound the Multi-class Bayes Error

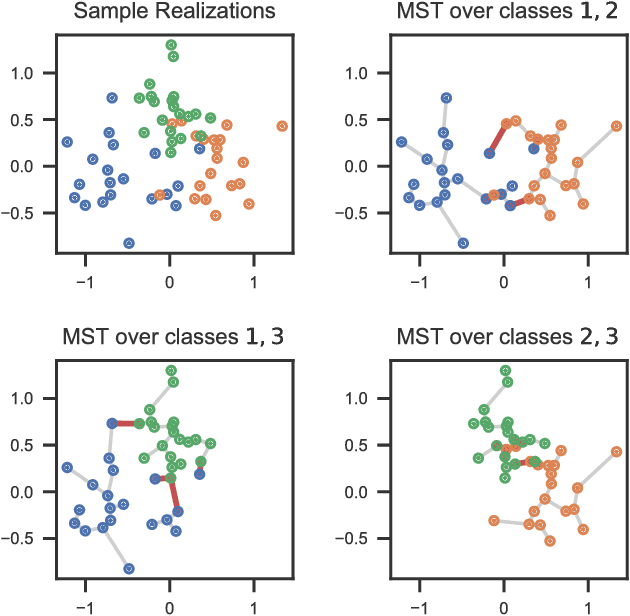
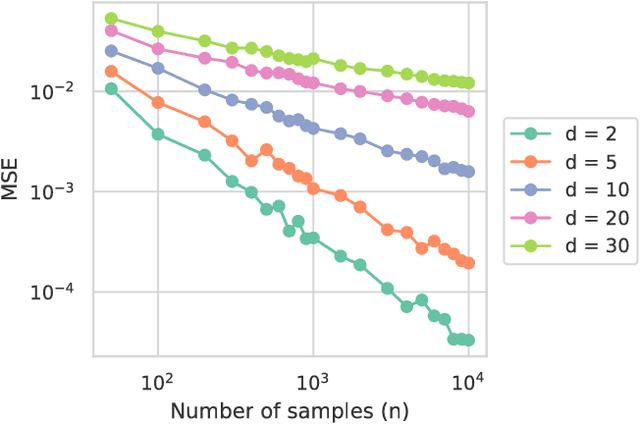
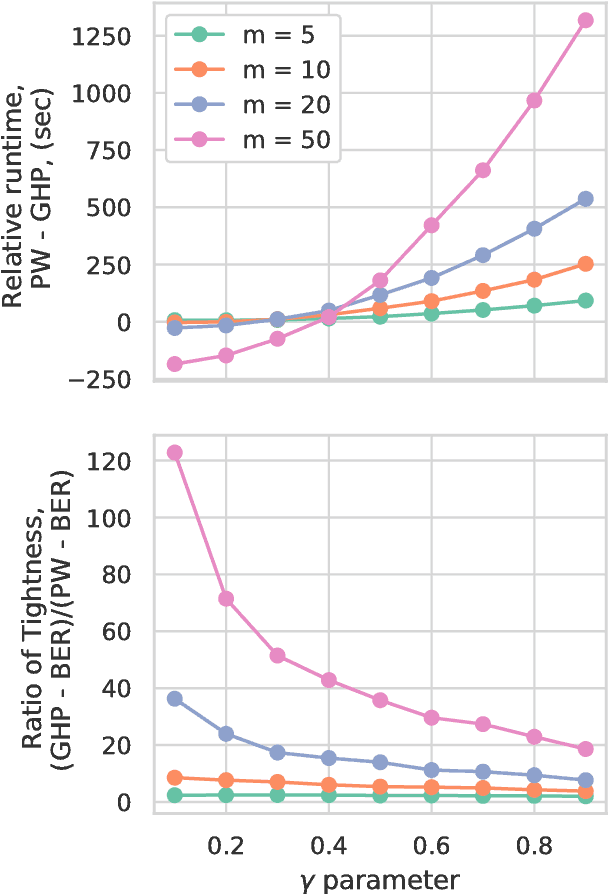
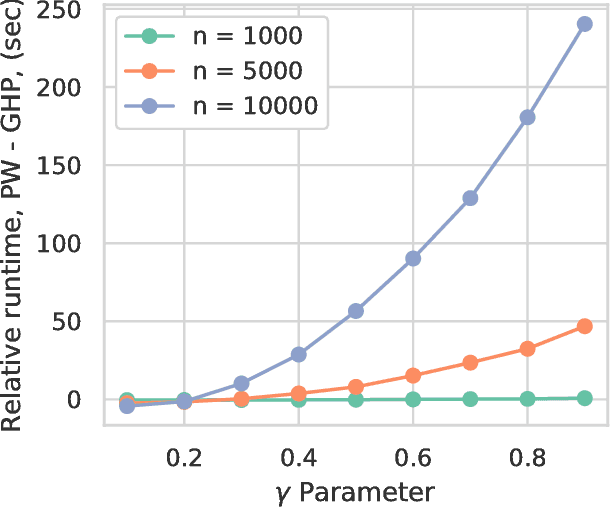
In the context of supervised learning, meta learning uses features, metadata and other information to learn about the difficulty, behavior, or composition of the problem. Using this knowledge can be useful to contextualize classifier results or allow for targeted decisions about future data sampling. In this paper, we are specifically interested in learning the Bayes error rate (BER) based on a labeled data sample. Providing a tight bound on the BER that is also feasible to estimate has been a challenge. Previous work [1] has shown that a pairwise bound based on the sum of Henze-Penrose (HP) divergence over label pairs can be directly estimated using a sum of Friedman-Rafsky (FR) multivariate run test statistics. However, in situations in which the dataset and number of classes are large, this bound is computationally infeasible to calculate and may not be tight. Other multi-class bounds also suffer from computationally complex estimation procedures. In this paper, we present a generalized HP divergence measure that allows us to estimate the Bayes error rate with log-linear computation. We prove that the proposed bound is tighter than both the pairwise method and a bound proposed by Lin [2]. We also empirically show that these bounds are close to the BER. We illustrate the proposed method on the MNIST dataset, and show its utility for the evaluation of feature reduction strategies.

Consistent Alignment of Word Embedding Models

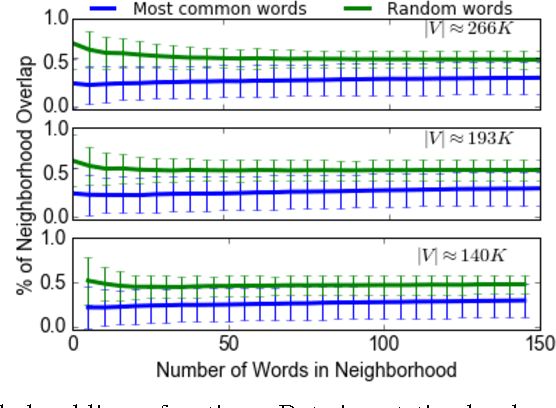
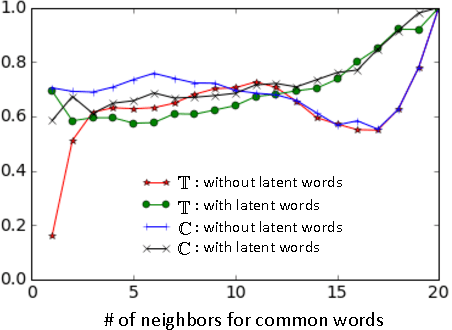
Word embedding models offer continuous vector representations that can capture rich contextual semantics based on their word co-occurrence patterns. While these word vectors can provide very effective features used in many NLP tasks such as clustering similar words and inferring learning relationships, many challenges and open research questions remain. In this paper, we propose a solution that aligns variations of the same model (or different models) in a joint low-dimensional latent space leveraging carefully generated synthetic data points. This generative process is inspired by the observation that a variety of linguistic relationships is captured by simple linear operations in embedded space. We demonstrate that our approach can lead to substantial improvements in recovering embeddings of local neighborhoods.

Similarity Function Tracking using Pairwise Comparisons

Recent work in distance metric learning has focused on learning transformations of data that best align with specified pairwise similarity and dissimilarity constraints, often supplied by a human observer. The learned transformations lead to improved retrieval, classification, and clustering algorithms due to the better adapted distance or similarity measures. Here, we address the problem of learning these transformations when the underlying constraint generation process is nonstationary. This nonstationarity can be due to changes in either the ground-truth clustering used to generate constraints or changes in the feature subspaces in which the class structure is apparent. We propose Online Convex Ensemble StrongLy Adaptive Dynamic Learning (OCELAD), a general adaptive, online approach for learning and tracking optimal metrics as they change over time that is highly robust to a variety of nonstationary behaviors in the changing metric. We apply the OCELAD framework to an ensemble of online learners. Specifically, we create a retro-initialized composite objective mirror descent (COMID) ensemble (RICE) consisting of a set of parallel COMID learners with different learning rates, and demonstrate parameter-free RICE-OCELAD metric learning on both synthetic data and a highly nonstationary Twitter dataset. We show significant performance improvements and increased robustness to nonstationary effects relative to previously proposed batch and online distance metric learning algorithms.