Learning to Bound the Multi-class Bayes Error
Paper and Code
Nov 15, 2018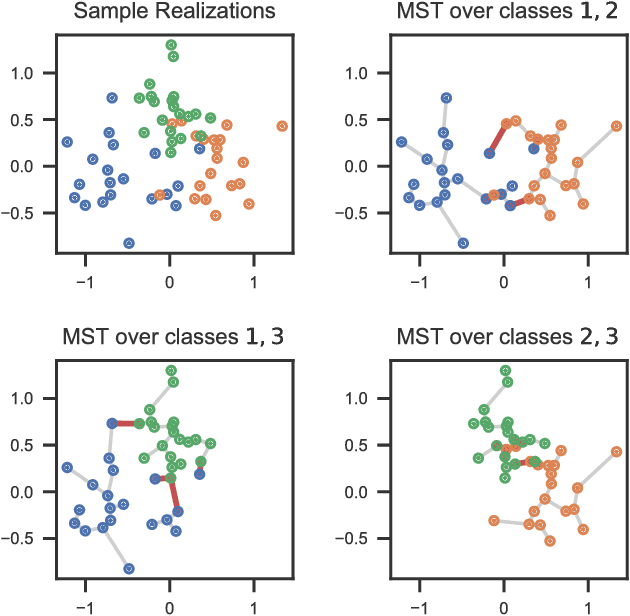
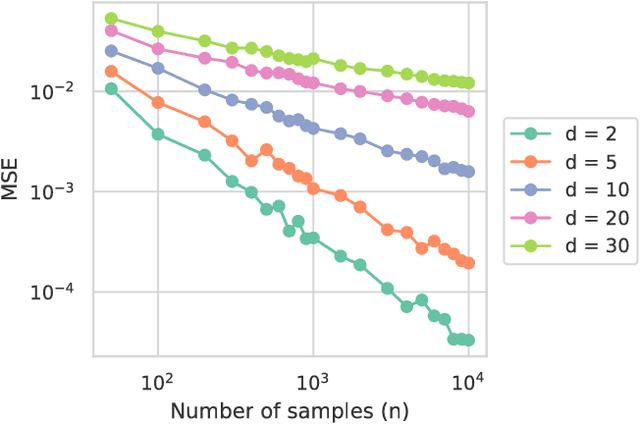
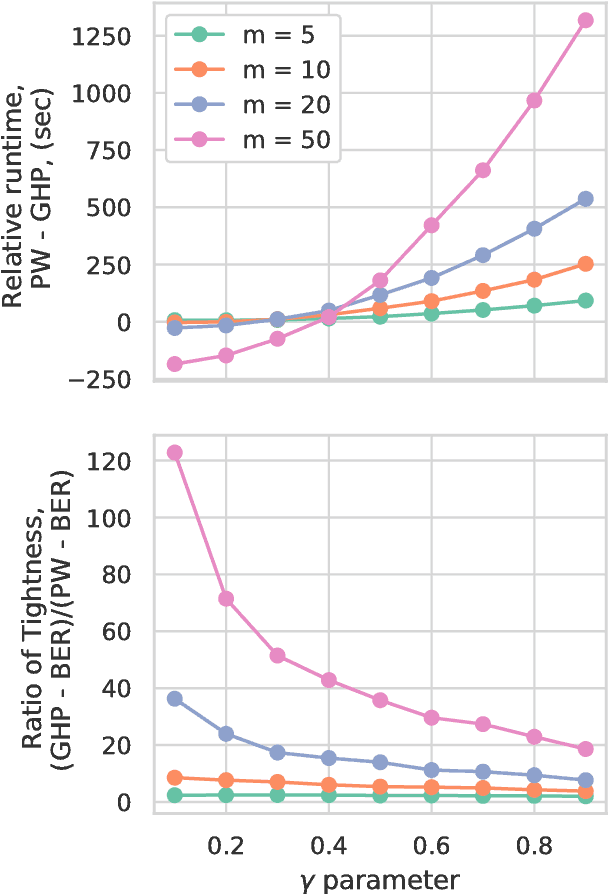
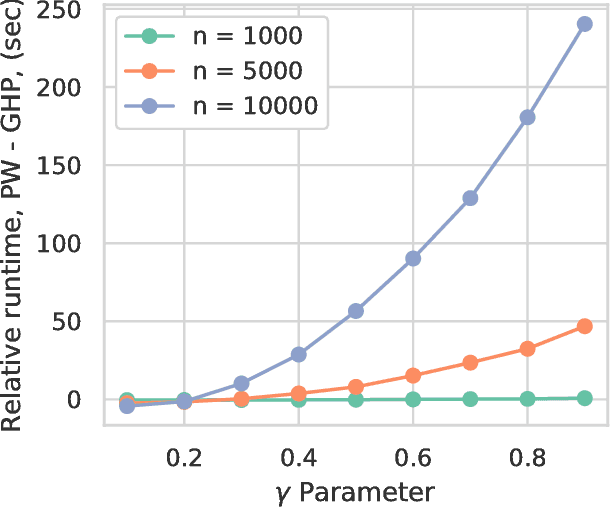
In the context of supervised learning, meta learning uses features, metadata and other information to learn about the difficulty, behavior, or composition of the problem. Using this knowledge can be useful to contextualize classifier results or allow for targeted decisions about future data sampling. In this paper, we are specifically interested in learning the Bayes error rate (BER) based on a labeled data sample. Providing a tight bound on the BER that is also feasible to estimate has been a challenge. Previous work [1] has shown that a pairwise bound based on the sum of Henze-Penrose (HP) divergence over label pairs can be directly estimated using a sum of Friedman-Rafsky (FR) multivariate run test statistics. However, in situations in which the dataset and number of classes are large, this bound is computationally infeasible to calculate and may not be tight. Other multi-class bounds also suffer from computationally complex estimation procedures. In this paper, we present a generalized HP divergence measure that allows us to estimate the Bayes error rate with log-linear computation. We prove that the proposed bound is tighter than both the pairwise method and a bound proposed by Lin [2]. We also empirically show that these bounds are close to the BER. We illustrate the proposed method on the MNIST dataset, and show its utility for the evaluation of feature reduction strategies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge