Geometric Estimation of Multivariate Dependency
Paper and Code
May 21, 2019
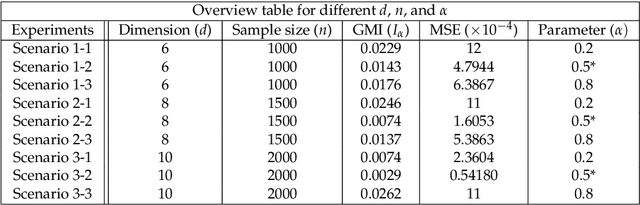
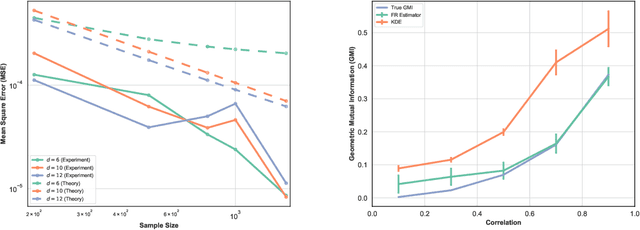
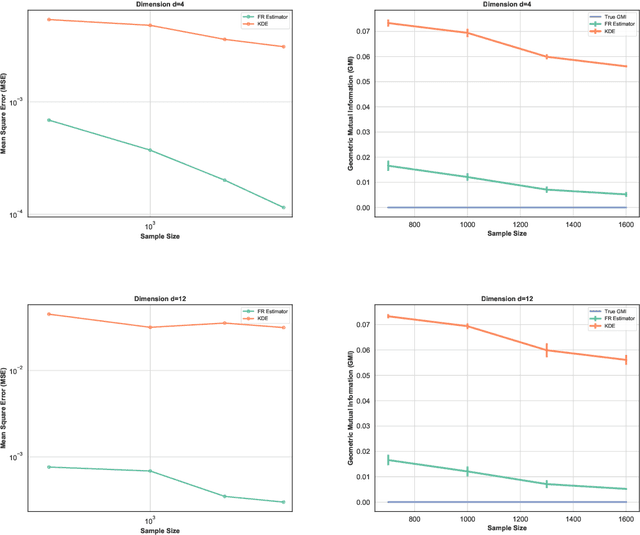
This paper proposes a geometric estimator of dependency between a pair of multivariate samples. The proposed estimator of dependency is based on a randomly permuted geometric graph (the minimal spanning tree) over the two multivariate samples. This estimator converges to a quantity that we call the geometric mutual information (GMI), which is equivalent to the Henze-Penrose divergence [1] between the joint distribution of the multivariate samples and the product of the marginals. The GMI has many of the same properties as standard MI but can be estimated from empirical data without density estimation; making it scalable to large datasets. The proposed empirical estimator of GMI is simple to implement, involving the construction of an MST spanning over both the original data and a randomly permuted version of this data. We establish asymptotic convergence of the estimator and convergence rates of the bias and variance for smooth multivariate density functions belonging to a H\"{o}lder class. We demonstrate the advantages of our proposed geometric dependency estimator in a series of experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge