Lie Group Algebra Convolutional Filters

In this paper we propose a framework to leverage Lie group symmetries on arbitrary spaces exploiting algebraic signal processing (ASP). We show that traditional group convolutions are one particular instantiation of a more general Lie group algebra homomorphism associated to an algebraic signal model rooted in the Lie group algebra $L^{1}(G)$ for given Lie group $G$. Exploiting this fact, we decouple the discretization of the Lie group convolution elucidating two separate sampling instances: the filter and the signal. To discretize the filters, we exploit the exponential map that links a Lie group with its associated Lie algebra. We show that the discrete Lie group filter learned from the data determines a unique filter in $L^{1}(G)$, and we show how this uniqueness of representation is defined by the bandwidth of the filter given a spectral representation. We also derive error bounds for the approximations of the filters in $L^{1}(G)$ with respect to its learned discrete representations. The proposed framework allows the processing of signals on spaces of arbitrary dimension and where the actions of some elements of the group are not necessarily well defined. Finally, we show that multigraph convolutional signal models come as the natural discrete realization of Lie group signal processing models, and we use this connection to establish stability results for Lie group algebra filters. To evaluate numerically our results, we build neural networks with these filters and we apply them in multiple datasets, including a knot classification problem.

Algebraic Convolutional Filters on Lie Group Algebras

Group convolutional neural networks are a useful tool for utilizing symmetries known to be in a signal; however, they require that the signal is defined on the group itself. Existing approaches either work directly with group signals, or they impose a lifting step with heuristics to compute the convolution which can be computationally costly. Taking an algebraic signal processing perspective, we propose a novel convolutional filter from the Lie group algebra directly, thereby removing the need to lift altogether. Furthermore, we establish stability of the filter by drawing connections to multigraph signal processing. The proposed filter is evaluated on a classification problem on two datasets with $SO(3)$ group symmetries.

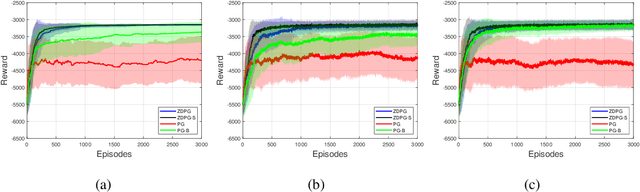
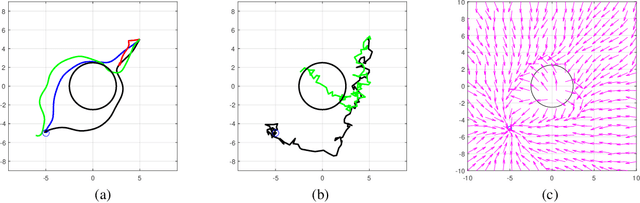
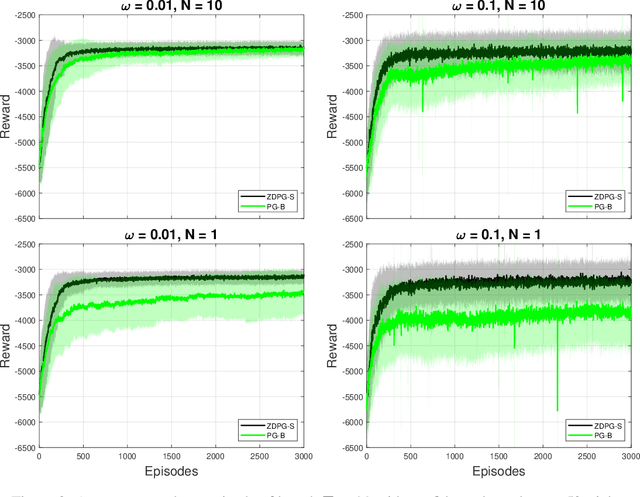
Zeroth-order Deterministic Policy Gradient

Deterministic Policy Gradient (DPG) removes a level of randomness from standard randomized-action Policy Gradient (PG), and demonstrates substantial empirical success for tackling complex dynamic problems involving Markov decision processes. At the same time, though, DPG loses its ability to learn in a model-free (i.e., actor-only) fashion, frequently necessitating the use of critics in order to obtain consistent estimates of the associated policy-reward gradient. In this work, we introduce Zeroth-order Deterministic Policy Gradient (ZDPG), which approximates policy-reward gradients via two-point stochastic evaluations of the $Q$-function, constructed by properly designed low-dimensional action-space perturbations. Exploiting the idea of random horizon rollouts for obtaining unbiased estimates of the $Q$-function, ZDPG lifts the dependence on critics and restores true model-free policy learning, while enjoying built-in and provable algorithmic stability. Additionally, we present new finite sample complexity bounds for ZDPG, which improve upon existing results by up to two orders of magnitude. Our findings are supported by several numerical experiments, which showcase the effectiveness of ZDPG in a practical setting, and its advantages over both PG and Baseline PG.

On the Sample Complexity of Actor-Critic Method for Reinforcement Learning with Function Approximation

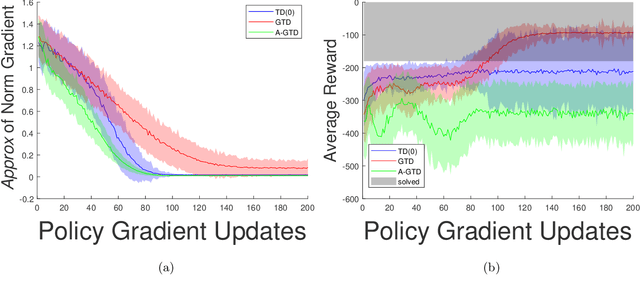
Reinforcement learning, mathematically described by Markov Decision Problems, may be approached either through dynamic programming or policy search. Actor-critic algorithms combine the merits of both approaches by alternating between steps to estimate the value function and policy gradient updates. Due to the fact that the updates exhibit correlated noise and biased gradient updates, only the asymptotic behavior of actor-critic is known by connecting its behavior to dynamical systems. This work puts forth a new variant of actor-critic that employs Monte Carlo rollouts during the policy search updates, which results in controllable bias that depends on the number of critic evaluations. As a result, we are able to provide for the first time the convergence rate of actor-critic algorithms when the policy search step employs policy gradient, agnostic to the choice of policy evaluation technique. In particular, we establish conditions under which the sample complexity is comparable to stochastic gradient method for non-convex problems or slower as a result of the critic estimation error, which is the main complexity bottleneck. These results hold for in continuous state and action spaces with linear function approximation for the value function. We then specialize these conceptual results to the case where the critic is estimated by Temporal Difference, Gradient Temporal Difference, and Accelerated Gradient Temporal Difference. These learning rates are then corroborated on a navigation problem involving an obstacle, which suggests that learning more slowly may lead to improved limit points, providing insight into the interplay between optimization and generalization in reinforcement learning.