Beyond variance reduction: Understanding the true impact of baselines on policy optimization

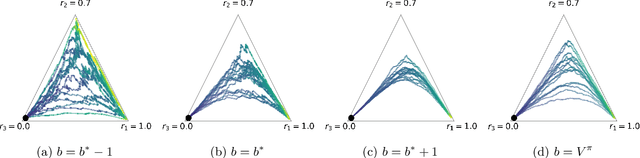
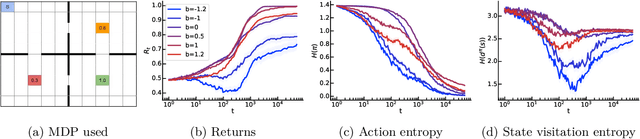
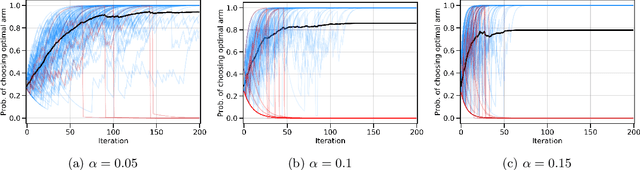
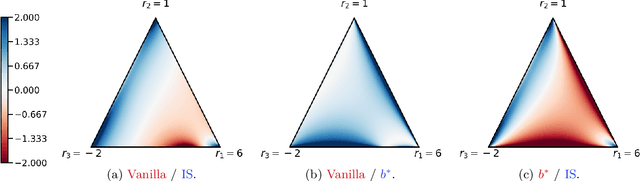
Policy gradients methods are a popular and effective choice to train reinforcement learning agents in complex environments. The variance of the stochastic policy gradient is often seen as a key quantity to determine the effectiveness of the algorithm. Baselines are a common addition to reduce the variance of the gradient, but previous works have hardly ever considered other effects baselines may have on the optimization process. Using simple examples, we find that baselines modify the optimization dynamics even when the variance is the same. In certain cases, a baseline with lower variance may even be worse than another with higher variance. Furthermore, we find that the choice of baseline can affect the convergence of natural policy gradient, where certain baselines may lead to convergence to a suboptimal policy for any stepsize. Such behaviour emerges when sampling is constrained to be done using the current policy and we show how decoupling the sampling policy from the current policy guarantees convergence for a much wider range of baselines. More broadly, this work suggests that a more careful treatment of stochasticity in the updates---beyond the immediate variance---is necessary to understand the optimization process of policy gradient algorithms.