Value-aware Importance Weighting for Off-policy Reinforcement Learning

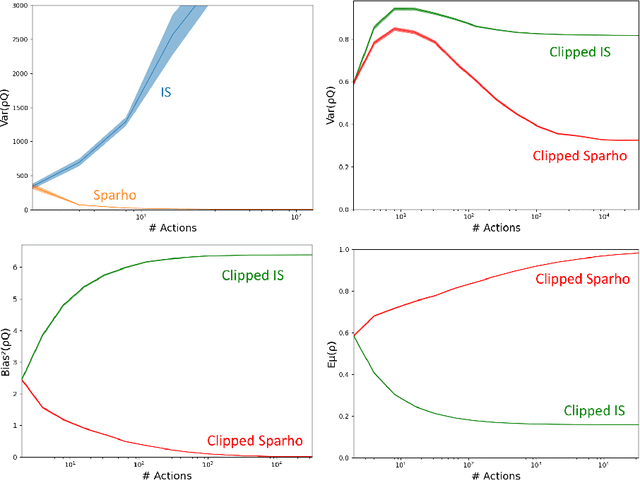
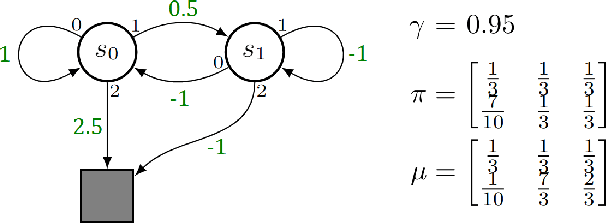
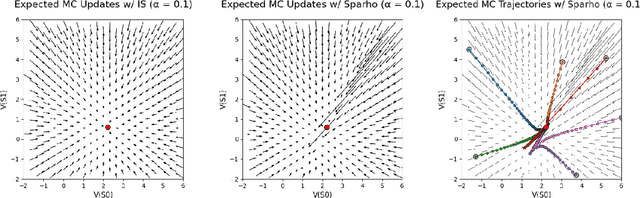
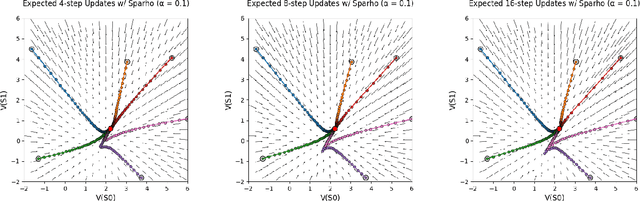
Importance sampling is a central idea underlying off-policy prediction in reinforcement learning. It provides a strategy for re-weighting samples from a distribution to obtain unbiased estimates under another distribution. However, importance sampling weights tend to exhibit extreme variance, often leading to stability issues in practice. In this work, we consider a broader class of importance weights to correct samples in off-policy learning. We propose the use of $\textit{value-aware importance weights}$ which take into account the sample space to provide lower variance, but still unbiased, estimates under a target distribution. We derive how such weights can be computed, and detail key properties of the resulting importance weights. We then extend several reinforcement learning prediction algorithms to the off-policy setting with these weights, and evaluate them empirically.

Importance Sampling Placement in Off-Policy Temporal-Difference Methods

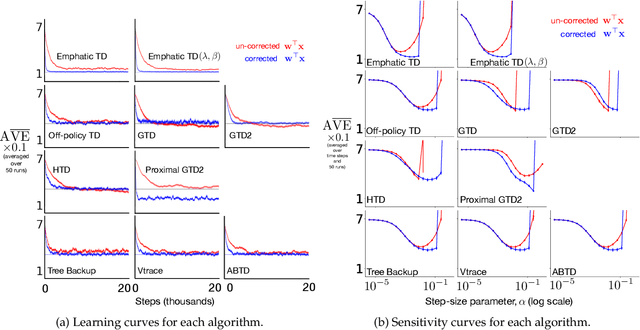
A central challenge to applying many off-policy reinforcement learning algorithms to real world problems is the variance introduced by importance sampling. In off-policy learning, the agent learns about a different policy than the one being executed. To account for the difference importance sampling ratios are often used, but can increase variance in the algorithms and reduce the rate of learning. Several variations of importance sampling have been proposed to reduce variance, with per-decision importance sampling being the most popular. However, the update rules for most off-policy algorithms in the literature depart from per-decision importance sampling in a subtle way; they correct the entire TD error instead of just the TD target. In this work, we show how this slight change can be interpreted as a control variate for the TD target, reducing variance and improving performance. Experiments over a wide range of algorithms show this subtle modification results in improved performance.

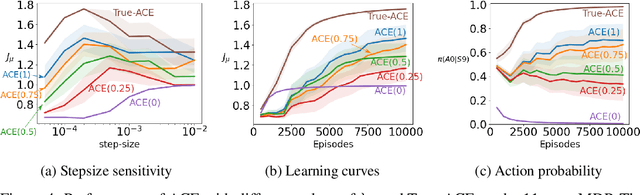
Off-Policy Actor-Critic with Emphatic Weightings

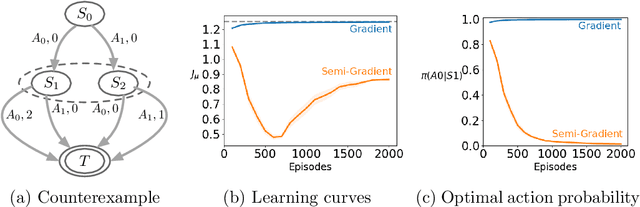
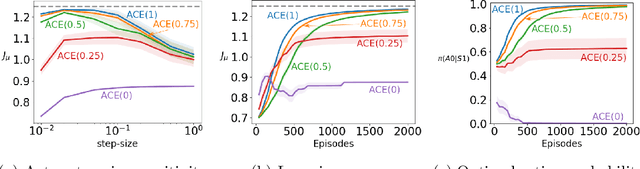
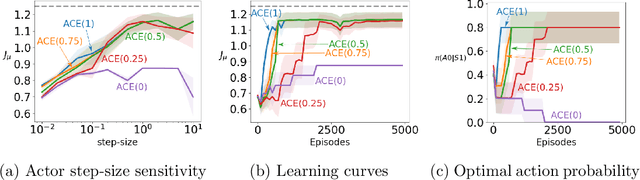
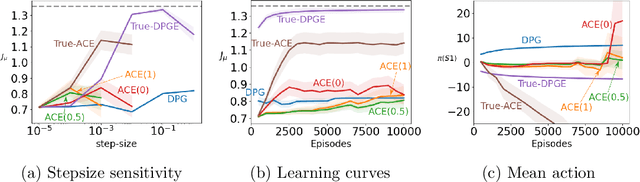
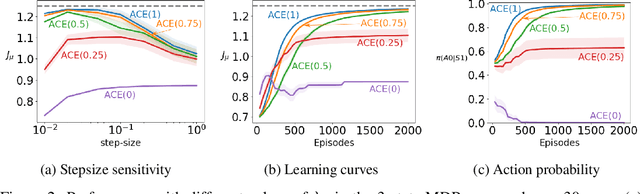
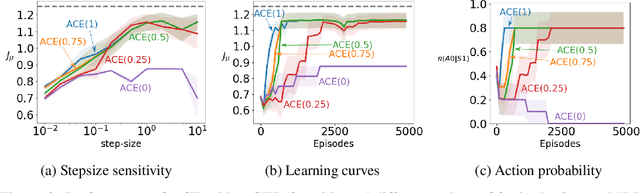
A variety of theoretically-sound policy gradient algorithms exist for the on-policy setting due to the policy gradient theorem, which provides a simplified form for the gradient. The off-policy setting, however, has been less clear due to the existence of multiple objectives and the lack of an explicit off-policy policy gradient theorem. In this work, we unify these objectives into one off-policy objective, and provide a policy gradient theorem for this unified objective. The derivation involves emphatic weightings and interest functions. We show multiple strategies to approximate the gradients, in an algorithm called Actor Critic with Emphatic weightings (ACE). We prove in a counterexample that previous (semi-gradient) off-policy actor-critic methods--particularly OffPAC and DPG--converge to the wrong solution whereas ACE finds the optimal solution. We also highlight why these semi-gradient approaches can still perform well in practice, suggesting strategies for variance reduction in ACE. We empirically study several variants of ACE on two classic control environments and an image-based environment designed to illustrate the tradeoffs made by each gradient approximation. We find that by approximating the emphatic weightings directly, ACE performs as well as or better than OffPAC in all settings tested.

An Off-policy Policy Gradient Theorem Using Emphatic Weightings

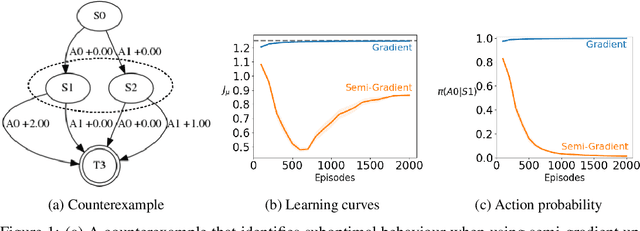
Policy gradient methods are widely used for control in reinforcement learning, particularly for the continuous action setting. There have been a host of theoretically sound algorithms proposed for the on-policy setting, due to the existence of the policy gradient theorem which provides a simplified form for the gradient. In off-policy learning, however, where the behaviour policy is not necessarily attempting to learn and follow the optimal policy for the given task, the existence of such a theorem has been elusive. In this work, we solve this open problem by providing the first off-policy policy gradient theorem. The key to the derivation is the use of $emphatic$ $weightings$. We develop a new actor-critic algorithm$\unicode{x2014}$called Actor Critic with Emphatic weightings (ACE)$\unicode{x2014}$that approximates the simplified gradients provided by the theorem. We demonstrate in a simple counterexample that previous off-policy policy gradient methods$\unicode{x2014}$particularly OffPAC and DPG$\unicode{x2014}$converge to the wrong solution whereas ACE finds the optimal solution.