Investigating the Histogram Loss in Regression

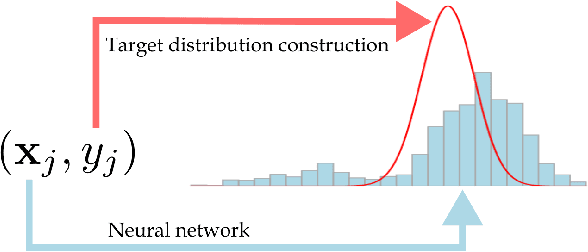
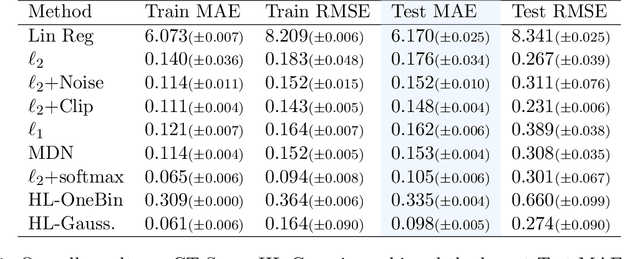
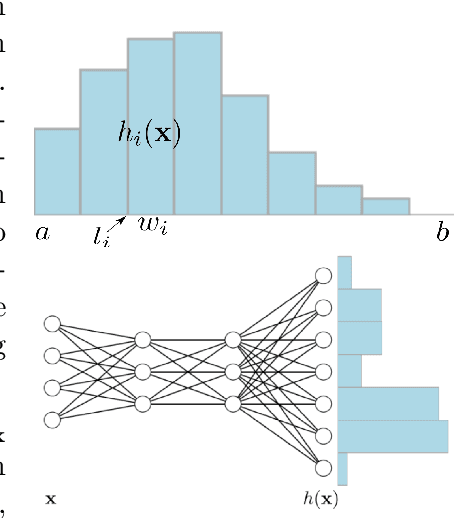
It is becoming increasingly common in regression to train neural networks that model the entire distribution even if only the mean is required for prediction. This additional modeling often comes with performance gain and the reasons behind the improvement are not fully known. This paper investigates a recent approach to regression, the Histogram Loss, which involves learning the conditional distribution of the target variable by minimizing the cross-entropy between a target distribution and a flexible histogram prediction. We design theoretical and empirical analyses to determine why and when this performance gain appears, and how different components of the loss contribute to it. Our results suggest that the benefits of learning distributions in this setup come from improvements in optimization rather than learning a better representation. We then demonstrate the viability of the Histogram Loss in common deep learning applications without a need for costly hyperparameter tuning.

The Tunnel Effect: Building Data Representations in Deep Neural Networks

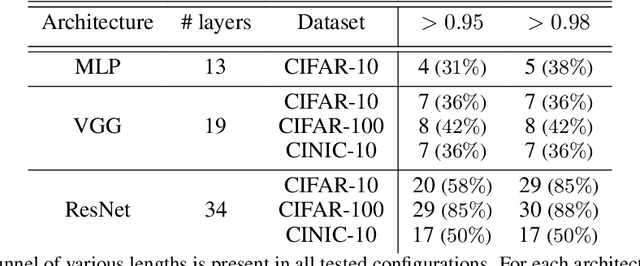
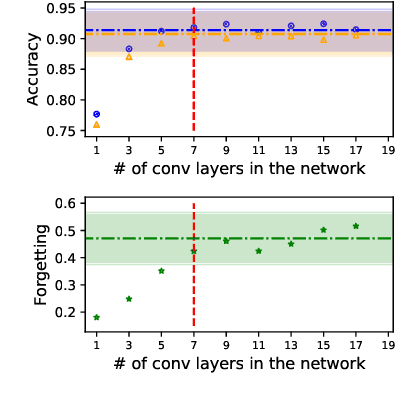
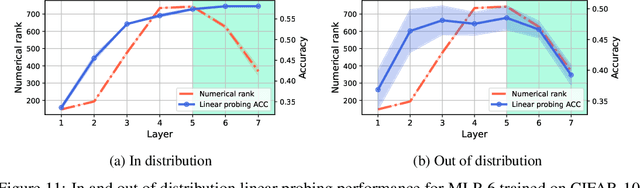
Deep neural networks are widely known for their remarkable effectiveness across various tasks, with the consensus that deeper networks implicitly learn more complex data representations. This paper shows that sufficiently deep networks trained for supervised image classification split into two distinct parts that contribute to the resulting data representations differently. The initial layers create linearly-separable representations, while the subsequent layers, which we refer to as \textit{the tunnel}, compress these representations and have a minimal impact on the overall performance. We explore the tunnel's behavior through comprehensive empirical studies, highlighting that it emerges early in the training process. Its depth depends on the relation between the network's capacity and task complexity. Furthermore, we show that the tunnel degrades out-of-distribution generalization and discuss its implications for continual learning.

Label Alignment Regularization for Distribution Shift

Recent work reported the label alignment property in a supervised learning setting: the vector of all labels in the dataset is mostly in the span of the top few singular vectors of the data matrix. Inspired by this observation, we derive a regularization method for unsupervised domain adaptation. Instead of regularizing representation learning as done by popular domain adaptation methods, we regularize the classifier so that the target domain predictions can to some extent ``align" with the top singular vectors of the unsupervised data matrix from the target domain. In a linear regression setting, we theoretically justify the label alignment property and characterize the optimality of the solution of our regularization by bounding its distance to the optimal solution. We conduct experiments to show that our method can work well on the label shift problems, where classic domain adaptation methods are known to fail. We also report mild improvement over domain adaptation baselines on a set of commonly seen MNIST-USPS domain adaptation tasks and on cross-lingual sentiment analysis tasks.

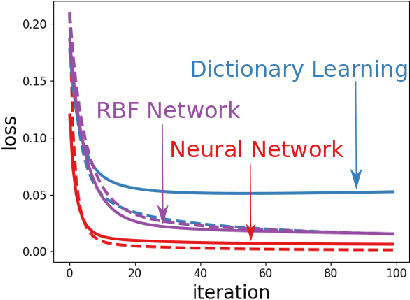
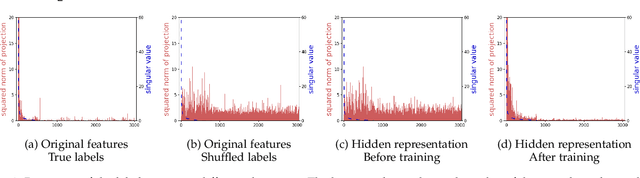
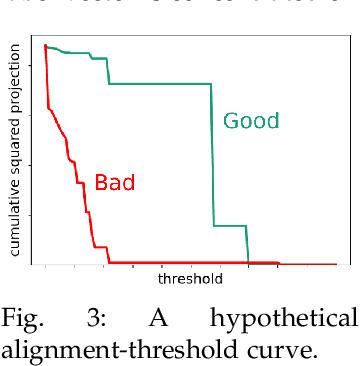
Understanding Feature Transfer Through Representation Alignment

Training with the true labels of a dataset as opposed to randomized labels leads to faster optimization and better generalization. This difference is attributed to a notion of alignment between inputs and labels in natural datasets. We find that training neural networks with different architectures and optimizers on random or true labels enforces the same relationship between the hidden representations and the training labels, elucidating why neural network representations have been so successful for transfer. We first highlight why aligned features promote transfer and show in a classic synthetic transfer problem that alignment is the determining factor for positive and negative transfer to similar and dissimilar tasks. We then investigate a variety of neural network architectures and find that (a) alignment emerges across a variety of different architectures and optimizers, with more alignment arising from depth (b) alignment increases for layers closer to the output and (c) existing high-performance deep CNNs exhibit high levels of alignment.

Off-Policy Actor-Critic with Emphatic Weightings

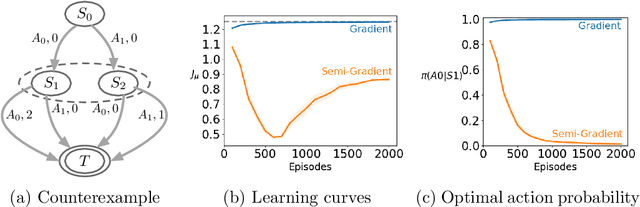
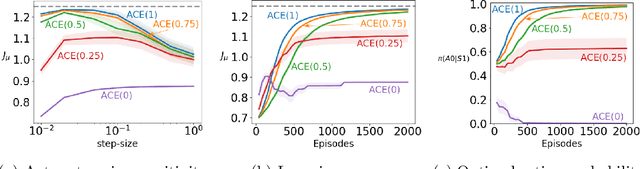
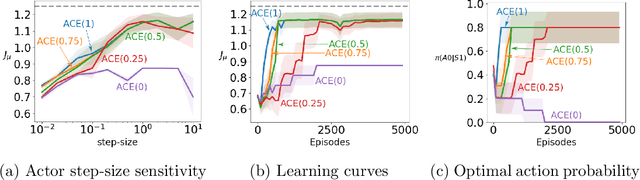
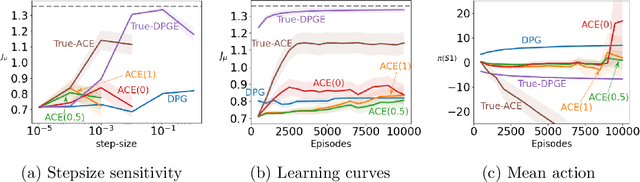
A variety of theoretically-sound policy gradient algorithms exist for the on-policy setting due to the policy gradient theorem, which provides a simplified form for the gradient. The off-policy setting, however, has been less clear due to the existence of multiple objectives and the lack of an explicit off-policy policy gradient theorem. In this work, we unify these objectives into one off-policy objective, and provide a policy gradient theorem for this unified objective. The derivation involves emphatic weightings and interest functions. We show multiple strategies to approximate the gradients, in an algorithm called Actor Critic with Emphatic weightings (ACE). We prove in a counterexample that previous (semi-gradient) off-policy actor-critic methods--particularly OffPAC and DPG--converge to the wrong solution whereas ACE finds the optimal solution. We also highlight why these semi-gradient approaches can still perform well in practice, suggesting strategies for variance reduction in ACE. We empirically study several variants of ACE on two classic control environments and an image-based environment designed to illustrate the tradeoffs made by each gradient approximation. We find that by approximating the emphatic weightings directly, ACE performs as well as or better than OffPAC in all settings tested.

Hallucinating Value: A Pitfall of Dyna-style Planning with Imperfect Environment Models

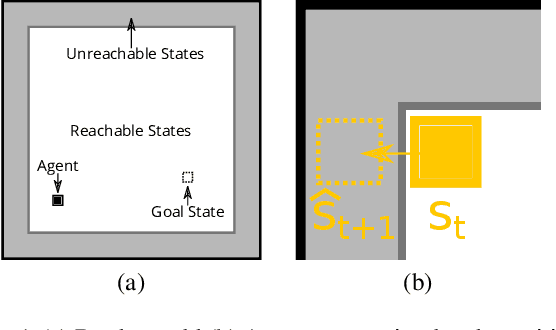
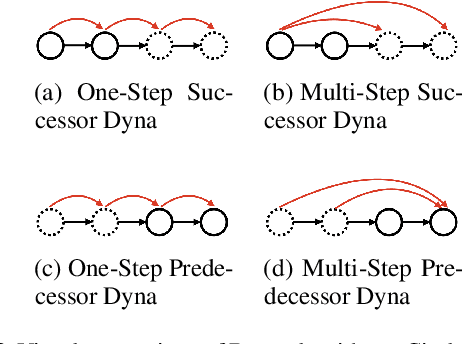
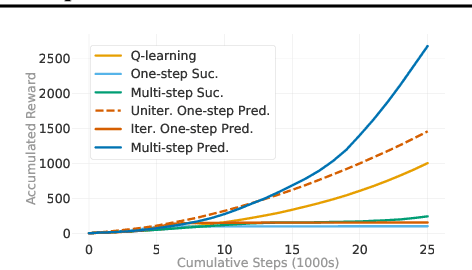
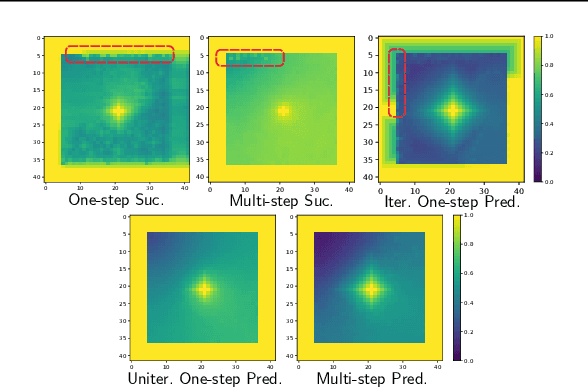
Dyna-style reinforcement learning (RL) agents improve sample efficiency over model-free RL agents by updating the value function with simulated experience generated by an environment model. However, it is often difficult to learn accurate models of environment dynamics, and even small errors may result in failure of Dyna agents. In this paper, we investigate one type of model error: hallucinated states. These are states generated by the model, but that are not real states of the environment. We present the Hallucinated Value Hypothesis (HVH): updating values of real states towards values of hallucinated states results in misleading state-action values which adversely affect the control policy. We discuss and evaluate four Dyna variants; three which update real states toward simulated -- and therefore potentially hallucinated -- states and one which does not. The experimental results provide evidence for the HVH thus suggesting a fruitful direction toward developing Dyna algorithms robust to model error.

An implicit function learning approach for parametric modal regression

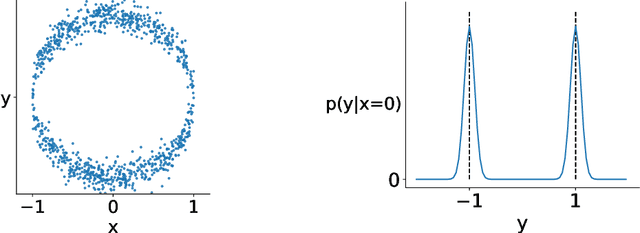
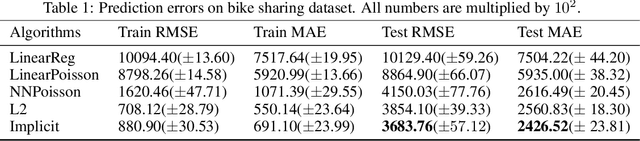
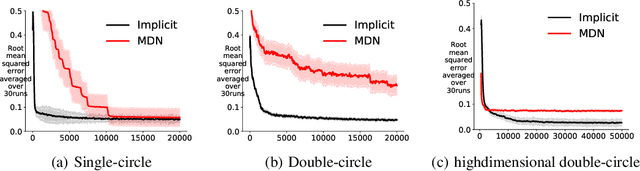
For multi-valued functions---such as when the conditional distribution on targets given the inputs is multi-modal---standard regression approaches are not always desirable because they provide the conditional mean. Modal regression aims to instead find the conditional mode, but is restricted to nonparametric approaches. Such methods can be difficult to scale, and cannot benefit from parametric function approximation, like neural networks, which can learn complex relationships between inputs and targets. In this work, we propose a parametric modal regression algorithm, by using the implicit function theorem to develop an objective for learning a joint parameterized function over inputs and targets. We empirically demonstrate on several synthetic problems that our method (i) can learn multi-valued functions and produce the conditional modes, (ii) scales well to high-dimensional inputs and (iii) is even more effective for certain uni-modal problems, particularly for high frequency data where the joint function over inputs and targets can better capture the complex relationship between them. We then demonstrate that our method is practically useful in a real-world modal regression problem. We conclude by showing that our method provides small improvements on two regression datasets that have asymmetric distributions over the targets.

An Off-policy Policy Gradient Theorem Using Emphatic Weightings

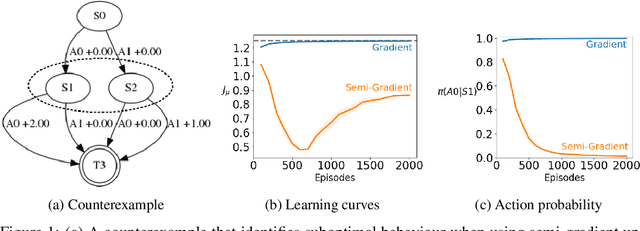
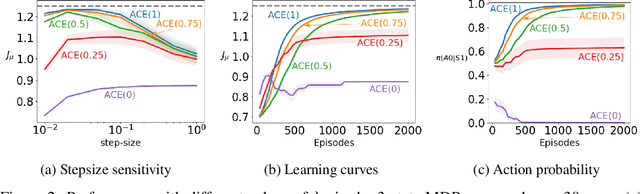
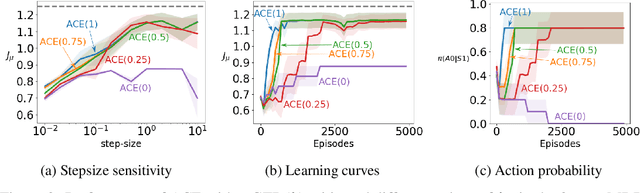
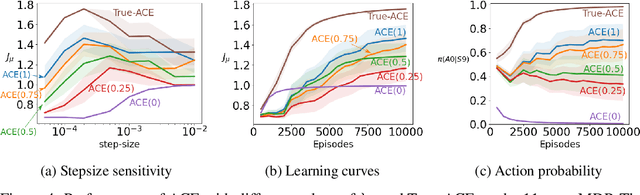
Policy gradient methods are widely used for control in reinforcement learning, particularly for the continuous action setting. There have been a host of theoretically sound algorithms proposed for the on-policy setting, due to the existence of the policy gradient theorem which provides a simplified form for the gradient. In off-policy learning, however, where the behaviour policy is not necessarily attempting to learn and follow the optimal policy for the given task, the existence of such a theorem has been elusive. In this work, we solve this open problem by providing the first off-policy policy gradient theorem. The key to the derivation is the use of $emphatic$ $weightings$. We develop a new actor-critic algorithm$\unicode{x2014}$called Actor Critic with Emphatic weightings (ACE)$\unicode{x2014}$that approximates the simplified gradients provided by the theorem. We demonstrate in a simple counterexample that previous off-policy policy gradient methods$\unicode{x2014}$particularly OffPAC and DPG$\unicode{x2014}$converge to the wrong solution whereas ACE finds the optimal solution.

Improving Regression Performance with Distributional Losses

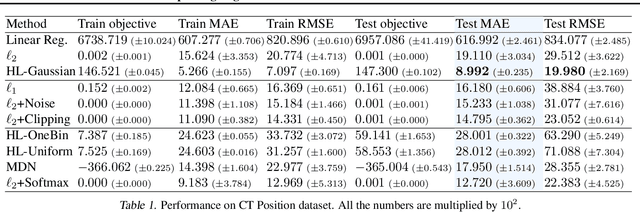
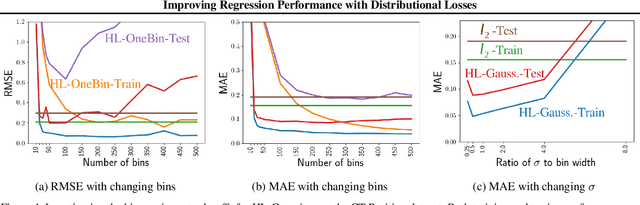
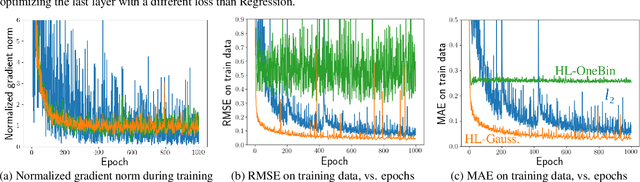
There is growing evidence that converting targets to soft targets in supervised learning can provide considerable gains in performance. Much of this work has considered classification, converting hard zero-one values to soft labels---such as by adding label noise, incorporating label ambiguity or using distillation. In parallel, there is some evidence from a regression setting in reinforcement learning that learning distributions can improve performance. In this work, we investigate the reasons for this improvement, in a regression setting. We introduce a novel distributional regression loss, and similarly find it significantly improves prediction accuracy. We investigate several common hypotheses, around reducing overfitting and improved representations. We instead find evidence for an alternative hypothesis: this loss is easier to optimize, with better behaved gradients, resulting in improved generalization. We provide theoretical support for this alternative hypothesis, by characterizing the norm of the gradients of this loss.