Investigating the Histogram Loss in Regression

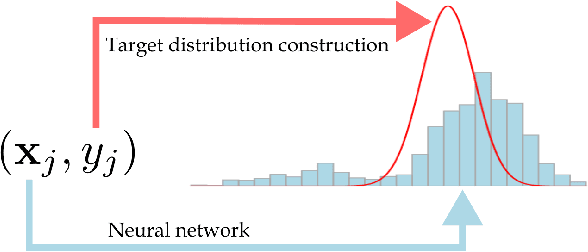
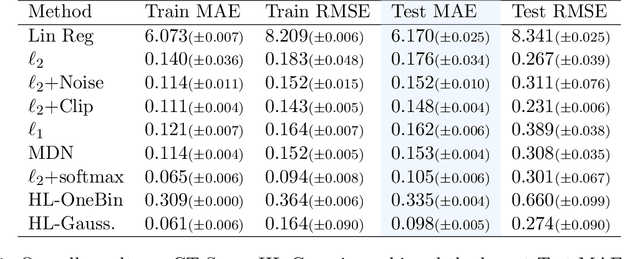
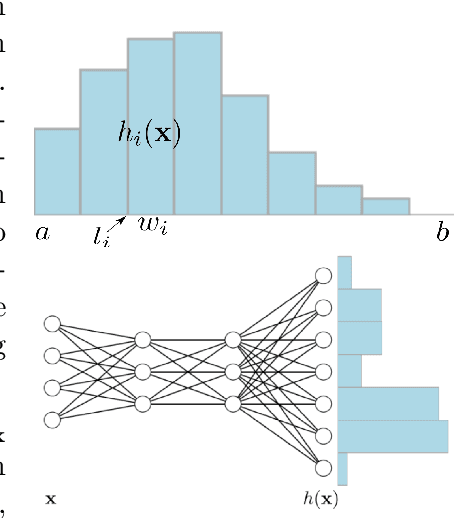
It is becoming increasingly common in regression to train neural networks that model the entire distribution even if only the mean is required for prediction. This additional modeling often comes with performance gain and the reasons behind the improvement are not fully known. This paper investigates a recent approach to regression, the Histogram Loss, which involves learning the conditional distribution of the target variable by minimizing the cross-entropy between a target distribution and a flexible histogram prediction. We design theoretical and empirical analyses to determine why and when this performance gain appears, and how different components of the loss contribute to it. Our results suggest that the benefits of learning distributions in this setup come from improvements in optimization rather than learning a better representation. We then demonstrate the viability of the Histogram Loss in common deep learning applications without a need for costly hyperparameter tuning.