An implicit function learning approach for parametric modal regression

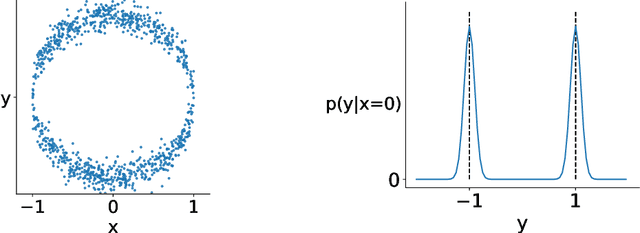
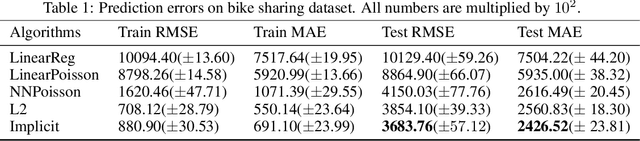
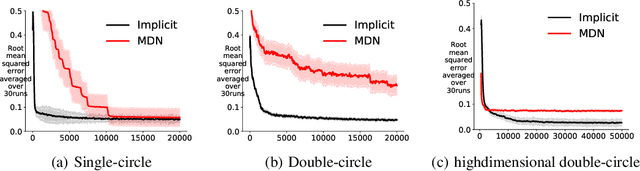
For multi-valued functions---such as when the conditional distribution on targets given the inputs is multi-modal---standard regression approaches are not always desirable because they provide the conditional mean. Modal regression aims to instead find the conditional mode, but is restricted to nonparametric approaches. Such methods can be difficult to scale, and cannot benefit from parametric function approximation, like neural networks, which can learn complex relationships between inputs and targets. In this work, we propose a parametric modal regression algorithm, by using the implicit function theorem to develop an objective for learning a joint parameterized function over inputs and targets. We empirically demonstrate on several synthetic problems that our method (i) can learn multi-valued functions and produce the conditional modes, (ii) scales well to high-dimensional inputs and (iii) is even more effective for certain uni-modal problems, particularly for high frequency data where the joint function over inputs and targets can better capture the complex relationship between them. We then demonstrate that our method is practically useful in a real-world modal regression problem. We conclude by showing that our method provides small improvements on two regression datasets that have asymmetric distributions over the targets.