Asynchronous Stochastic Approximation and Average-Reward Reinforcement Learning

This paper studies asynchronous stochastic approximation (SA) algorithms and their application to reinforcement learning in semi-Markov decision processes (SMDPs) with an average-reward criterion. We first extend Borkar and Meyn's stability proof method to accommodate more general noise conditions, leading to broader convergence guarantees for asynchronous SA algorithms. Leveraging these results, we establish the convergence of an asynchronous SA analogue of Schweitzer's classical relative value iteration algorithm, RVI Q-learning, for finite-space, weakly communicating SMDPs. Furthermore, to fully utilize the SA results in this application, we introduce new monotonicity conditions for estimating the optimal reward rate in RVI Q-learning. These conditions substantially expand the previously considered algorithmic framework, and we address them with novel proof arguments in the stability and convergence analysis of RVI Q-learning.

On Convergence of Average-Reward Q-Learning in Weakly Communicating Markov Decision Processes

This paper analyzes reinforcement learning (RL) algorithms for Markov decision processes (MDPs) under the average-reward criterion. We focus on Q-learning algorithms based on relative value iteration (RVI), which are model-free stochastic analogues of the classical RVI method for average-reward MDPs. These algorithms have low per-iteration complexity, making them well-suited for large state space problems. We extend the almost-sure convergence analysis of RVI Q-learning algorithms developed by Abounadi, Bertsekas, and Borkar (2001) from unichain to weakly communicating MDPs. This extension is important both practically and theoretically: weakly communicating MDPs cover a much broader range of applications compared to unichain MDPs, and their optimality equations have a richer solution structure (with multiple degrees of freedom), introducing additional complexity in proving algorithmic convergence. We also characterize the sets to which RVI Q-learning algorithms converge, showing that they are compact, connected, potentially nonconvex, and comprised of solutions to the average-reward optimality equation, with exactly one less degree of freedom than the general solution set of this equation. Furthermore, we extend our analysis to two RVI-based hierarchical average-reward RL algorithms using the options framework, proving their almost-sure convergence and characterizing their sets of convergence under the assumption that the underlying semi-Markov decision process is weakly communicating.

A Note on Stability in Asynchronous Stochastic Approximation without Communication Delays

In this paper, we study asynchronous stochastic approximation algorithms without communication delays. Our main contribution is a stability proof for these algorithms that extends a method of Borkar and Meyn by accommodating more general noise conditions. We also derive convergence results from this stability result and discuss their application in important average-reward reinforcement learning problems.

Two geometric input transformation methods for fast online reinforcement learning with neural nets

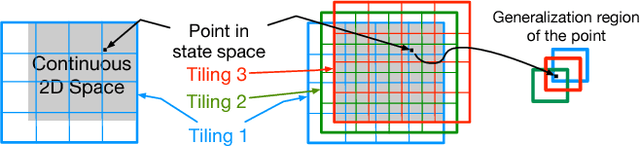
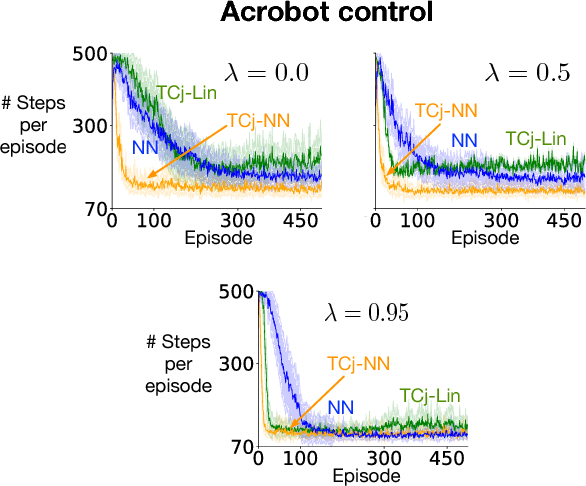
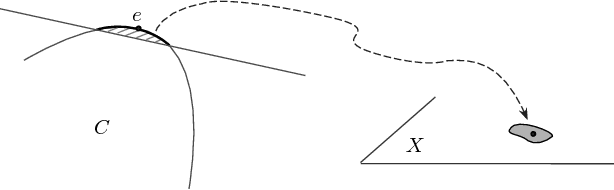
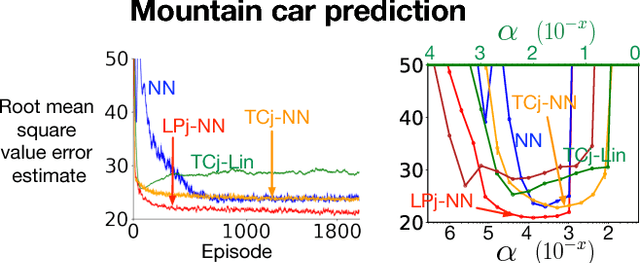
We apply neural nets with ReLU gates in online reinforcement learning. Our goal is to train these networks in an incremental manner, without the computationally expensive experience replay. By studying how individual neural nodes behave in online training, we recognize that the global nature of ReLU gates can cause undesirable learning interference in each node's learning behavior. We propose reducing such interferences with two efficient input transformation methods that are geometric in nature and match well the geometric property of ReLU gates. The first one is tile coding, a classic binary encoding scheme originally designed for local generalization based on the topological structure of the input space. The second one (EmECS) is a new method we introduce; it is based on geometric properties of convex sets and topological embedding of the input space into the boundary of a convex set. We discuss the behavior of the network when it operates on the transformed inputs. We also compare it experimentally with some neural nets that do not use the same input transformations, and with the classic algorithm of tile coding plus a linear function approximator, and on several online reinforcement learning tasks, we show that the neural net with tile coding or EmECS can achieve not only faster learning but also more accurate approximations. Our results strongly suggest that geometric input transformation of this type can be effective for interference reduction and takes us a step closer to fully incremental reinforcement learning with neural nets.

On Convergence of some Gradient-based Temporal-Differences Algorithms for Off-Policy Learning

We consider off-policy temporal-difference (TD) learning methods for policy evaluation in Markov decision processes with finite spaces and discounted reward criteria, and we present a collection of convergence results for several gradient-based TD algorithms with linear function approximation. The algorithms we analyze include: (i) two basic forms of two-time-scale gradient-based TD algorithms, which we call GTD and which minimize the mean squared projected Bellman error using stochastic gradient-descent; (ii) their "robustified" biased variants; (iii) their mirror-descent versions which combine the mirror-descent idea with TD learning; and (iv) a single-time-scale version of GTD that solves minimax problems formulated for approximate policy evaluation. We derive convergence results for three types of stepsizes: constant stepsize, slowly diminishing stepsize, as well as the standard type of diminishing stepsize with a square-summable condition. For the first two types of stepsizes, we apply the weak convergence method from stochastic approximation theory to characterize the asymptotic behavior of the algorithms, and for the standard type of stepsize, we analyze the algorithmic behavior with respect to a stronger mode of convergence, almost sure convergence. Our convergence results are for the aforementioned TD algorithms with three general ways of setting their $\lambda$-parameters: (i) state-dependent $\lambda$; (ii) a recently proposed scheme of using history-dependent $\lambda$ to keep the eligibility traces of the algorithms bounded while allowing for relatively large values of $\lambda$; and (iii) a composite scheme of setting the $\lambda$-parameters that combines the preceding two schemes and allows a broader class of generalized Bellman operators to be used for approximate policy evaluation with TD methods.

On Convergence of Emphatic Temporal-Difference Learning

We consider emphatic temporal-difference learning algorithms for policy evaluation in discounted Markov decision processes with finite spaces. Such algorithms were recently proposed by Sutton, Mahmood, and White (2015) as an improved solution to the problem of divergence of off-policy temporal-difference learning with linear function approximation. We present in this paper the first convergence proofs for two emphatic algorithms, ETD($\lambda$) and ELSTD($\lambda$). We prove, under general off-policy conditions, the convergence in $L^1$ for ELSTD($\lambda$) iterates, and the almost sure convergence of the approximate value functions calculated by both algorithms using a single infinitely long trajectory. Our analysis involves new techniques with applications beyond emphatic algorithms leading, for example, to the first proof that standard TD($\lambda$) also converges under off-policy training for $\lambda$ sufficiently large.

Multi-step Off-policy Learning Without Importance Sampling Ratios

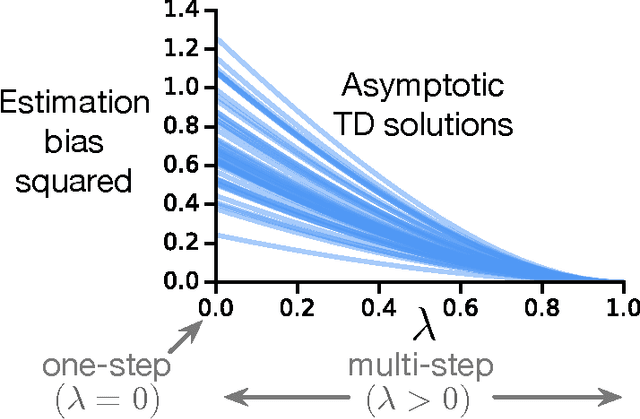
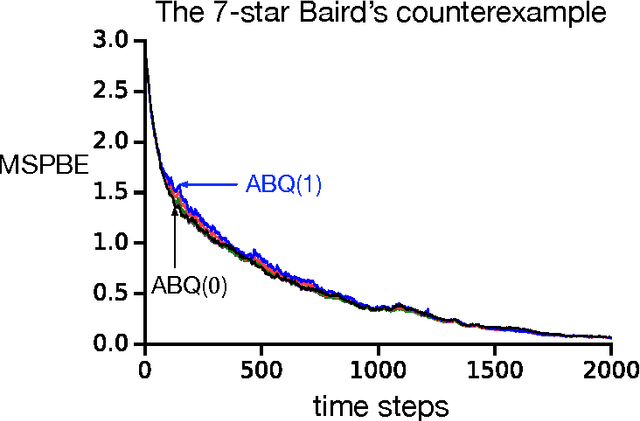
To estimate the value functions of policies from exploratory data, most model-free off-policy algorithms rely on importance sampling, where the use of importance sampling ratios often leads to estimates with severe variance. It is thus desirable to learn off-policy without using the ratios. However, such an algorithm does not exist for multi-step learning with function approximation. In this paper, we introduce the first such algorithm based on temporal-difference (TD) learning updates. We show that an explicit use of importance sampling ratios can be eliminated by varying the amount of bootstrapping in TD updates in an action-dependent manner. Our new algorithm achieves stability using a two-timescale gradient-based TD update. A prior algorithm based on lookup table representation called Tree Backup can also be retrieved using action-dependent bootstrapping, becoming a special case of our algorithm. In two challenging off-policy tasks, we demonstrate that our algorithm is stable, effectively avoids the large variance issue, and can perform substantially better than its state-of-the-art counterpart.

Weak Convergence Properties of Constrained Emphatic Temporal-difference Learning with Constant and Slowly Diminishing Stepsize

We consider the emphatic temporal-difference (TD) algorithm, ETD($\lambda$), for learning the value functions of stationary policies in a discounted, finite state and action Markov decision process. The ETD($\lambda$) algorithm was recently proposed by Sutton, Mahmood, and White to solve a long-standing divergence problem of the standard TD algorithm when it is applied to off-policy training, where data from an exploratory policy are used to evaluate other policies of interest. The almost sure convergence of ETD($\lambda$) has been proved in our recent work under general off-policy training conditions, but for a narrow range of diminishing stepsize. In this paper we present convergence results for constrained versions of ETD($\lambda$) with constant stepsize and with diminishing stepsize from a broad range. Our results characterize the asymptotic behavior of the trajectory of iterates produced by those algorithms, and are derived by combining key properties of ETD($\lambda$) with powerful convergence theorems from the weak convergence methods in stochastic approximation theory. For the case of constant stepsize, in addition to analyzing the behavior of the algorithms in the limit as the stepsize parameter approaches zero, we also analyze their behavior for a fixed stepsize and bound the deviations of their averaged iterates from the desired solution. These results are obtained by exploiting the weak Feller property of the Markov chains associated with the algorithms, and by using ergodic theorems for weak Feller Markov chains, in conjunction with the convergence results we get from the weak convergence methods. Besides ETD($\lambda$), our analysis also applies to the off-policy TD($\lambda$) algorithm, when the divergence issue is avoided by setting $\lambda$ sufficiently large.

Some Simulation Results for Emphatic Temporal-Difference Learning Algorithms

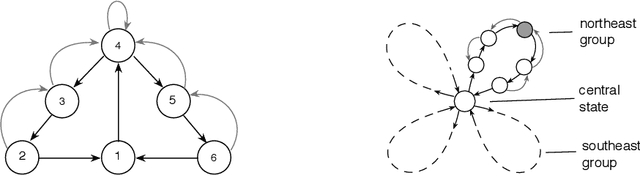
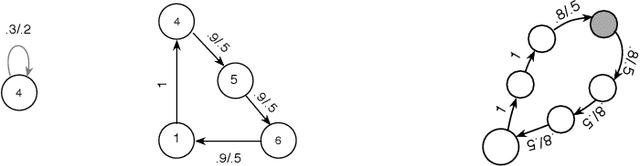
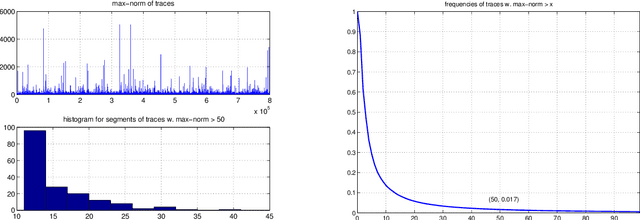
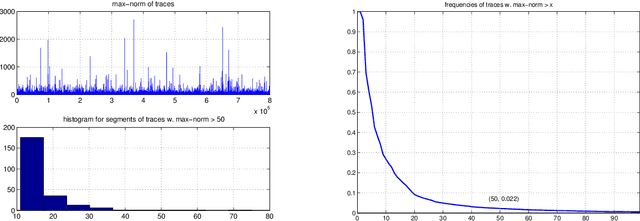
This is a companion note to our recent study of the weak convergence properties of constrained emphatic temporal-difference learning (ETD) algorithms from a theoretic perspective. It supplements the latter analysis with simulation results and illustrates the behavior of some of the ETD algorithms using three example problems.

Emphatic Temporal-Difference Learning

Emphatic algorithms are temporal-difference learning algorithms that change their effective state distribution by selectively emphasizing and de-emphasizing their updates on different time steps. Recent works by Sutton, Mahmood and White (2015), and Yu (2015) show that by varying the emphasis in a particular way, these algorithms become stable and convergent under off-policy training with linear function approximation. This paper serves as a unified summary of the available results from both works. In addition, we demonstrate the empirical benefits from the flexibility of emphatic algorithms, including state-dependent discounting, state-dependent bootstrapping, and the user-specified allocation of function approximation resources.