Multi-step Off-policy Learning Without Importance Sampling Ratios
Paper and Code
Feb 09, 2017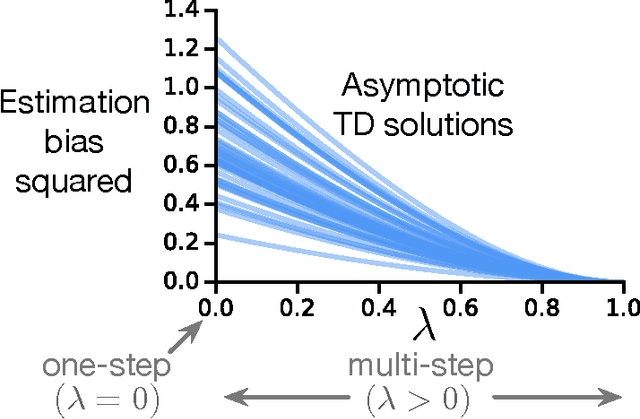


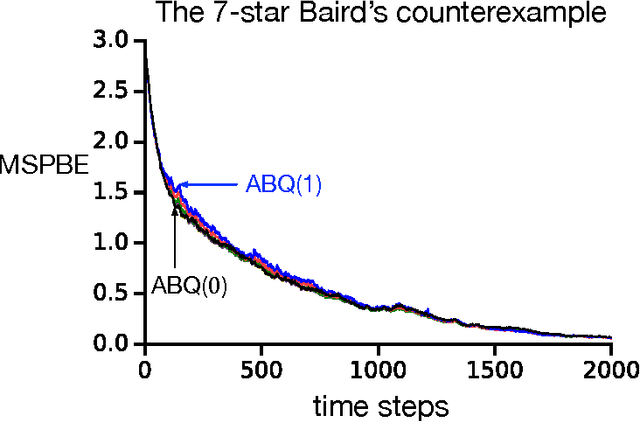
To estimate the value functions of policies from exploratory data, most model-free off-policy algorithms rely on importance sampling, where the use of importance sampling ratios often leads to estimates with severe variance. It is thus desirable to learn off-policy without using the ratios. However, such an algorithm does not exist for multi-step learning with function approximation. In this paper, we introduce the first such algorithm based on temporal-difference (TD) learning updates. We show that an explicit use of importance sampling ratios can be eliminated by varying the amount of bootstrapping in TD updates in an action-dependent manner. Our new algorithm achieves stability using a two-timescale gradient-based TD update. A prior algorithm based on lookup table representation called Tree Backup can also be retrieved using action-dependent bootstrapping, becoming a special case of our algorithm. In two challenging off-policy tasks, we demonstrate that our algorithm is stable, effectively avoids the large variance issue, and can perform substantially better than its state-of-the-art counterpart.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge