An Idiosyncrasy of Time-discretization in Reinforcement Learning
Paper and Code
Jun 21, 2024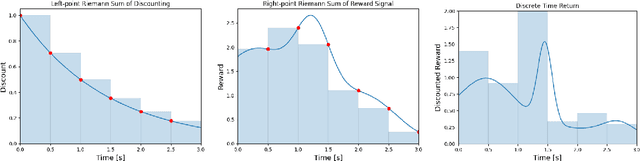
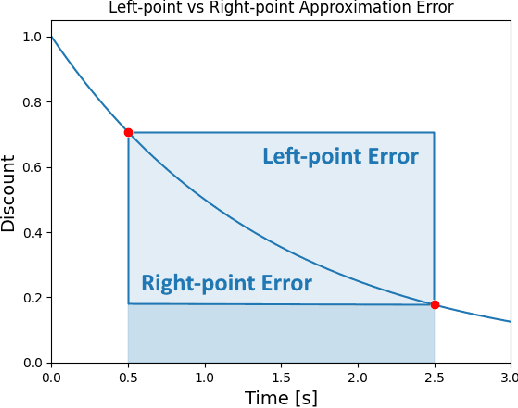
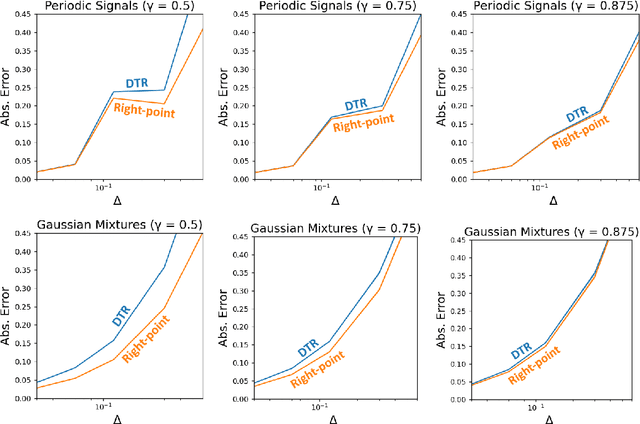
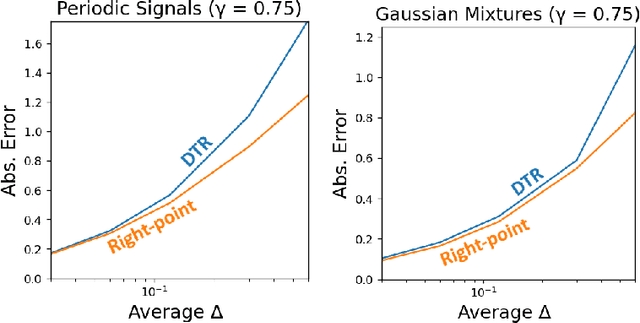
Many reinforcement learning algorithms are built on an assumption that an agent interacts with an environment over fixed-duration, discrete time steps. However, physical systems are continuous in time, requiring a choice of time-discretization granularity when digitally controlling them. Furthermore, such systems do not wait for decisions to be made before advancing the environment state, necessitating the study of how the choice of discretization may affect a reinforcement learning algorithm. In this work, we consider the relationship between the definitions of the continuous-time and discrete-time returns. Specifically, we acknowledge an idiosyncrasy with naively applying a discrete-time algorithm to a discretized continuous-time environment, and note how a simple modification can better align the return definitions. This observation is of practical consideration when dealing with environments where time-discretization granularity is a choice, or situations where such granularity is inherently stochastic.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge