A computational scheme for Reasoning in Dynamic Probabilistic Networks

A computational scheme for reasoning about dynamic systems using (causal) probabilistic networks is presented. The scheme is based on the framework of Lauritzen and Spiegelhalter (1988), and may be viewed as a generalization of the inference methods of classical time-series analysis in the sense that it allows description of non-linear, multivariate dynamic systems with complex conditional independence structures. Further, the scheme provides a method for efficient backward smoothing and possibilities for efficient, approximate forecasting methods. The scheme has been implemented on top of the HUGIN shell.

Reduction of Computational Complexity in Bayesian Networks through Removal of Weak Dependencies

The paper presents a method for reducing the computational complexity of Bayesian networks through identification and removal of weak dependencies (removal of links from the (moralized) independence graph). The removal of a small number of links may reduce the computational complexity dramatically, since several fill-ins and moral links may be rendered superfluous by the removal. The method is described in terms of impact on the independence graph, the junction tree, and the potential functions associated with these. An empirical evaluation of the method using large real-world networks demonstrates the applicability of the method. Further, the method, which has been implemented in Hugin, complements the approximation method suggested by Jensen & Andersen (1990).

HUGS: Combining Exact Inference and Gibbs Sampling in Junction Trees

Dawid, Kjaerulff and Lauritzen (1994) provided a preliminary description of a hybrid between Monte-Carlo sampling methods and exact local computations in junction trees. Utilizing the strengths of both methods, such hybrid inference methods has the potential of expanding the class of problems which can be solved under bounded resources as well as solving problems which otherwise resist exact solutions. The paper provides a detailed description of a particular instance of such a hybrid scheme; namely, combination of exact inference and Gibbs sampling in discrete Bayesian networks. We argue that this combination calls for an extension of the usual message passing scheme of ordinary junction trees.

Nested Junction Trees

The efficiency of inference in both the Hugin and, most notably, the Shafer-Shenoy architectures can be improved by exploiting the independence relations induced by the incoming messages of a clique. That is, the message to be sent from a clique can be computed via a factorization of the clique potential in the form of a junction tree. In this paper we show that by exploiting such nested junction trees in the computation of messages both space and time costs of the conventional propagation methods may be reduced. The paper presents a structured way of exploiting the nested junction trees technique to achieve such reductions. The usefulness of the method is emphasized through a thorough empirical evaluation involving ten large real-world Bayesian networks and the Hugin inference algorithm.

Using ROBDDs for Inference in Bayesian Networks with Troubleshooting as an Example

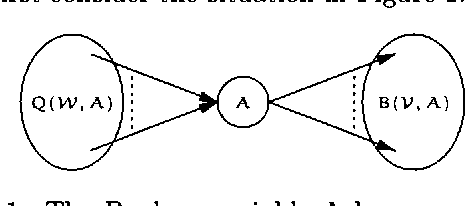
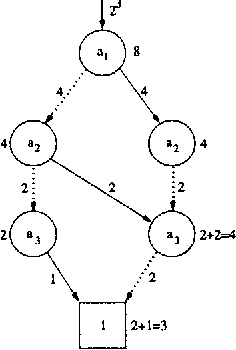
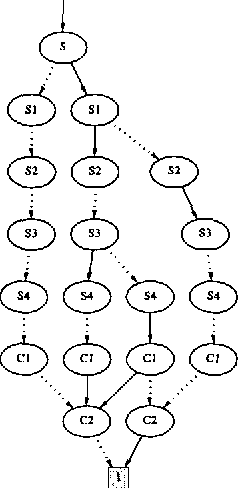
When using Bayesian networks for modelling the behavior of man-made machinery, it usually happens that a large part of the model is deterministic. For such Bayesian networks deterministic part of the model can be represented as a Boolean function, and a central part of belief updating reduces to the task of calculating the number of satisfying configurations in a Boolean function. In this paper we explore how advances in the calculation of Boolean functions can be adopted for belief updating, in particular within the context of troubleshooting. We present experimental results indicating a substantial speed-up compared to traditional junction tree propagation.

Making Sensitivity Analysis Computationally Efficient

To investigate the robustness of the output probabilities of a Bayesian network, a sensitivity analysis can be performed. A one-way sensitivity analysis establishes, for each of the probability parameters of a network, a function expressing a posterior marginal probability of interest in terms of the parameter. Current methods for computing the coefficients in such a function rely on a large number of network evaluations. In this paper, we present a method that requires just a single outward propagation in a junction tree for establishing the coefficients in the functions for all possible parameters; in addition, an inward propagation is required for processing evidence. Conversely, the method requires a single outward propagation for computing the coefficients in the functions expressing all possible posterior marginals in terms of a single parameter. We extend these results to an n-way sensitivity analysis in which sets of parameters are studied.