Computing Probability Intervals Under Independency Constraints

Many AI researchers argue that probability theory is only capable of dealing with uncertainty in situations where a full specification of a joint probability distribution is available, and conclude that it is not suitable for application in knowledge-based systems. Probability intervals, however, constitute a means for expressing incompleteness of information. We present a method for computing such probability intervals for probabilities of interest from a partial specification of a joint probability distribution. Our method improves on earlier approaches by allowing for independency relationships between statistical variables to be exploited.

Elicitation of Probabilities for Belief Networks: Combining Qualitative and Quantitative Information

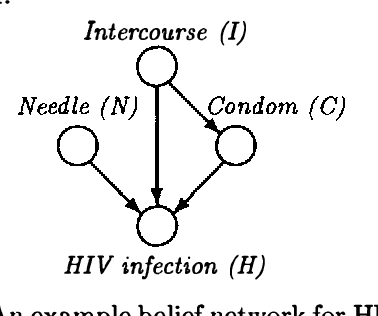
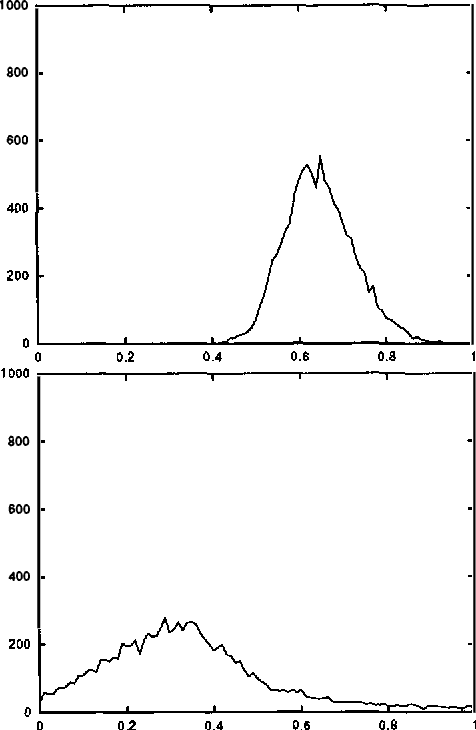
Although the usefulness of belief networks for reasoning under uncertainty is widely accepted, obtaining numerical probabilities that they require is still perceived a major obstacle. Often not enough statistical data is available to allow for reliable probability estimation. Available information may not be directly amenable for encoding in the network. Finally, domain experts may be reluctant to provide numerical probabilities. In this paper, we propose a method for elicitation of probabilities from a domain expert that is non-invasive and accommodates whatever probabilistic information the expert is willing to state. We express all available information, whether qualitative or quantitative in nature, in a canonical form consisting of (in) equalities expressing constraints on the hyperspace of possible joint probability distributions. We then use this canonical form to derive second-order probability distributions over the desired probabilities.

How to Elicit Many Probabilities

In building Bayesian belief networks, the elicitation of all probabilities required can be a major obstacle. We learned the extent of this often-cited observation in the construction of the probabilistic part of a complex influence diagram in the field of cancer treatment. Based upon our negative experiences with existing methods, we designed a new method for probability elicitation from domain experts. The method combines various ideas, among which are the ideas of transcribing probabilities and of using a scale with both numerical and verbal anchors for marking assessments. In the construction of the probabilistic part of our influence diagram, the method proved to allow for the elicitation of many probabilities in little time.

Enhancing QPNs for Trade-off Resolution

Qualitative probabilistic networks have been introduced as qualitative abstractions of Bayesian belief networks. One of the major drawbacks of these qualitative networks is their coarse level of detail, which may lead to unresolved trade-offs during inference. We present an enhanced formalism for qualitative networks with a finer level of detail. An enhanced qualitative probabilistic network differs from a regular qualitative network in that it distinguishes between strong and weak influences. Enhanced qualitative probabilistic networks are purely qualitative in nature, as regular qualitative networks are, yet allow for efficiently resolving trade-offs during inference.

Pivotal Pruning of Trade-offs in QPNs

Qualitative probabilistic networks have been designed for probabilistic reasoning in a qualitative way. Due to their coarse level of representation detail, qualitative probabilistic networks do not provide for resolving trade-offs and typically yield ambiguous results upon inference. We present an algorithm for computing more insightful results for unresolved trade-offs. The algorithm builds upon the idea of using pivots to zoom in on the trade-offs and identifying the information that would serve to resolve them.

Making Sensitivity Analysis Computationally Efficient

To investigate the robustness of the output probabilities of a Bayesian network, a sensitivity analysis can be performed. A one-way sensitivity analysis establishes, for each of the probability parameters of a network, a function expressing a posterior marginal probability of interest in terms of the parameter. Current methods for computing the coefficients in such a function rely on a large number of network evaluations. In this paper, we present a method that requires just a single outward propagation in a junction tree for establishing the coefficients in the functions for all possible parameters; in addition, an inward propagation is required for processing evidence. Conversely, the method requires a single outward propagation for computing the coefficients in the functions expressing all possible posterior marginals in terms of a single parameter. We extend these results to an n-way sensitivity analysis in which sets of parameters are studied.

Analysing Sensitivity Data from Probabilistic Networks

With the advance of efficient analytical methods for sensitivity analysis ofprobabilistic networks, the interest in the sensitivities revealed by real-life networks is rekindled. As the amount of data resulting from a sensitivity analysis of even a moderately-sized network is alreadyoverwhelming, methods for extracting relevant information are called for. One such methodis to study the derivative of the sensitivity functions yielded for a network's parameters. We further propose to build upon the concept of admissible deviation, that is, the extent to which a parameter can deviate from the true value without inducing a change in the most likely outcome. We illustrate these concepts by means of a sensitivity analysis of a real-life probabilistic network in oncology.

Pre-processing for Triangulation of Probabilistic Networks

The currently most efficient algorithm for inference with a probabilistic network builds upon a triangulation of a network's graph. In this paper, we show that pre-processing can help in finding good triangulations forprobabilistic networks, that is, triangulations with a minimal maximum clique size. We provide a set of rules for stepwise reducing a graph, without losing optimality. This reduction allows us to solve the triangulation problem on a smaller graph. From the smaller graph's triangulation, a triangulation of the original graph is obtained by reversing the reduction steps. Our experimental results show that the graphs of some well-known real-life probabilistic networks can be triangulated optimally just by preprocessing; for other networks, huge reductions in their graph's size are obtained.

From Qualitative to Quantitative Probabilistic Networks

Quantification is well known to be a major obstacle in the construction of a probabilistic network, especially when relying on human experts for this purpose. The construction of a qualitative probabilistic network has been proposed as an initial step in a network s quantification, since the qualitative network can be used TO gain preliminary insight IN the projected networks reasoning behaviour. We extend on this idea and present a new type of network in which both signs and numbers are specified; we further present an associated algorithm for probabilistic inference. Building upon these semi-qualitative networks, a probabilistic network can be quantified and studied in a stepwise manner. As a result, modelling inadequacies can be detected and amended at an early stage in the quantification process.

Upgrading Ambiguous Signs in QPNs

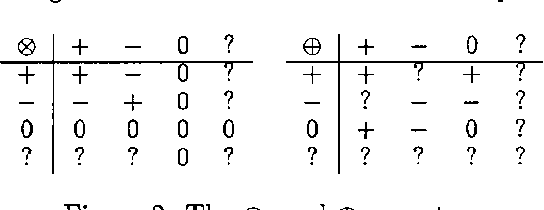
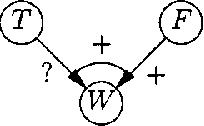
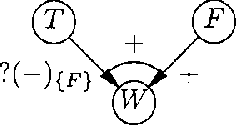
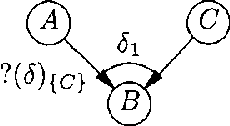
WA qualitative probabilistic network models the probabilistic relationships between its variables by means of signs. Non-monotonic influences have associated an ambiguous sign. These ambiguous signs typically lead to uninformative results upon inference. A non-monotonic influence can, however, be associated with a, more informative, sign that indicates its effect in the current state of the network. To capture this effect, we introduce the concept of situational sign. Furthermore, if the network converts to a state in which all variables that provoke the non-monotonicity have been observed, a non-monotonic influence reduces to a monotonic influence. We study the persistence and propagation of situational signs upon inference and give a method to establish the sign of a reduced influence.