Elicitation of Probabilities for Belief Networks: Combining Qualitative and Quantitative Information
Paper and Code
Feb 20, 2013
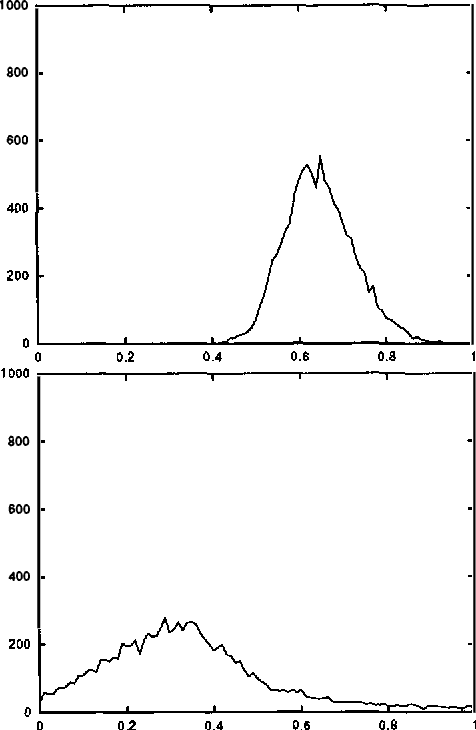
Although the usefulness of belief networks for reasoning under uncertainty is widely accepted, obtaining numerical probabilities that they require is still perceived a major obstacle. Often not enough statistical data is available to allow for reliable probability estimation. Available information may not be directly amenable for encoding in the network. Finally, domain experts may be reluctant to provide numerical probabilities. In this paper, we propose a method for elicitation of probabilities from a domain expert that is non-invasive and accommodates whatever probabilistic information the expert is willing to state. We express all available information, whether qualitative or quantitative in nature, in a canonical form consisting of (in) equalities expressing constraints on the hyperspace of possible joint probability distributions. We then use this canonical form to derive second-order probability distributions over the desired probabilities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge