Marek J. Druzdzel
Qualitative Propagation and Scenario-based Explanation of Probabilistic Reasoning
Mar 27, 2013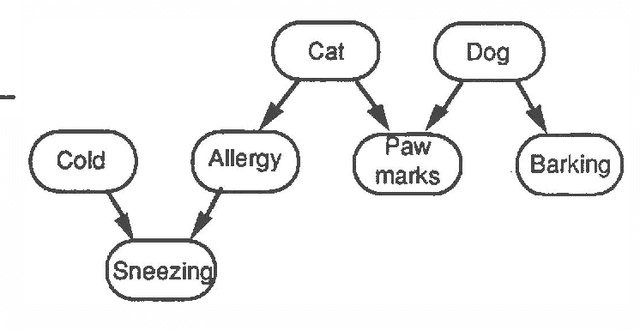


Abstract:Comprehensible explanations of probabilistic reasoning are a prerequisite for wider acceptance of Bayesian methods in expert systems and decision support systems. A study of human reasoning under uncertainty suggests two different strategies for explaining probabilistic reasoning: The first, qualitative belief propagation, traces the qualitative effect of evidence through a belief network from one variable to the next. This propagation algorithm is an alternative to the graph reduction algorithms of Wellman (1988) for inference in qualitative probabilistic networks. It is based on a qualitative analysis of intercausal reasoning, which is a generalization of Pearl's "explaining away", and an alternative to Wellman's definition of qualitative synergy. The other, Scenario-based reasoning, involves the generation of alternative causal "stories" accounting for the evidence. Comparing a few of the most probable scenarios provides an approximate way to explain the results of probabilistic reasoning. Both schemes employ causal as well as probabilistic knowledge. Probabilities may be presented as phrases and/or numbers. Users can control the style, abstraction and completeness of explanations.
Intercausal Reasoning with Uninstantiated Ancestor Nodes
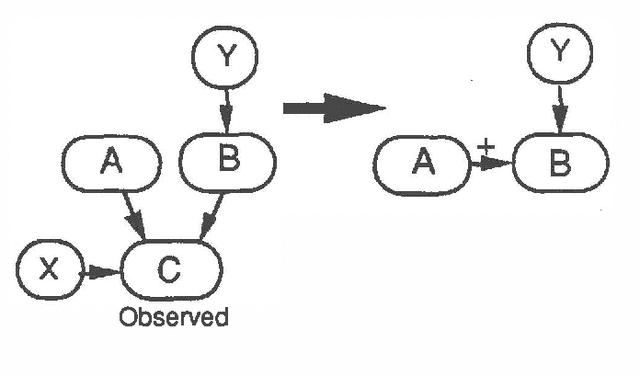
Mar 06, 2013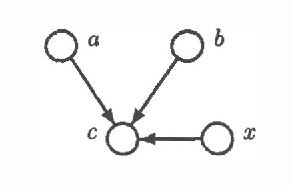
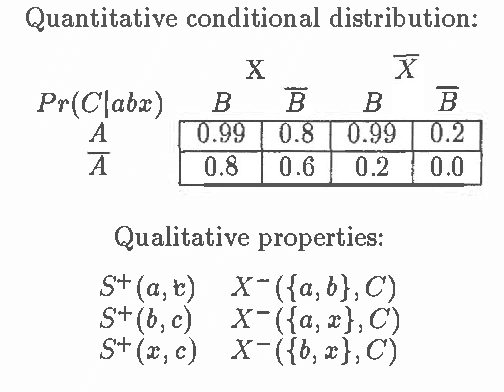
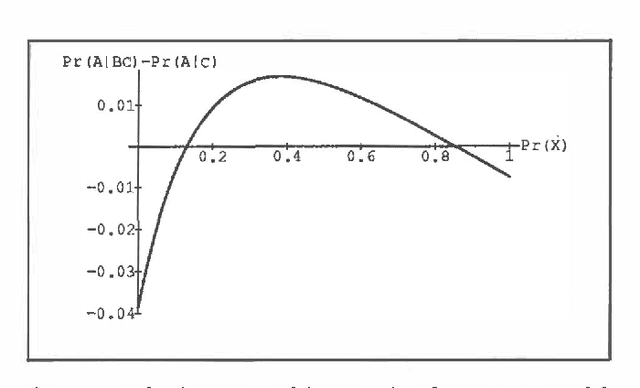
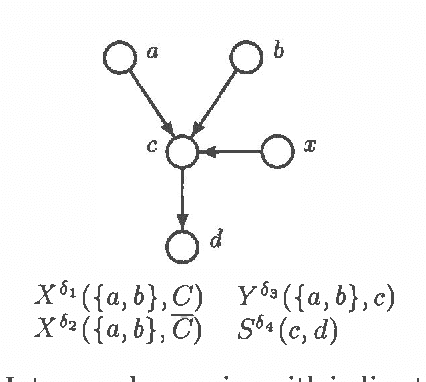
Abstract:Intercausal reasoning is a common inference pattern involving probabilistic dependence of causes of an observed common effect. The sign of this dependence is captured by a qualitative property called product synergy. The current definition of product synergy is insufficient for intercausal reasoning where there are additional uninstantiated causes of the common effect. We propose a new definition of product synergy and prove its adequacy for intercausal reasoning with direct and indirect evidence for the common effect. The new definition is based on a new property matrix half positive semi-definiteness, a weakened form of matrix positive semi-definiteness.
Causality in Bayesian Belief Networks
Mar 06, 2013Abstract:We address the problem of causal interpretation of the graphical structure of Bayesian belief networks (BBNs). We review the concept of causality explicated in the domain of structural equations models and show that it is applicable to BBNs. In this view, which we call mechanism-based, causality is defined within models and causal asymmetries arise when mechanisms are placed in the context of a system. We lay the link between structural equations models and BBNs models and formulate the conditions under which the latter can be given causal interpretation.
Some Properties of Joint Probability Distributions
Feb 27, 2013
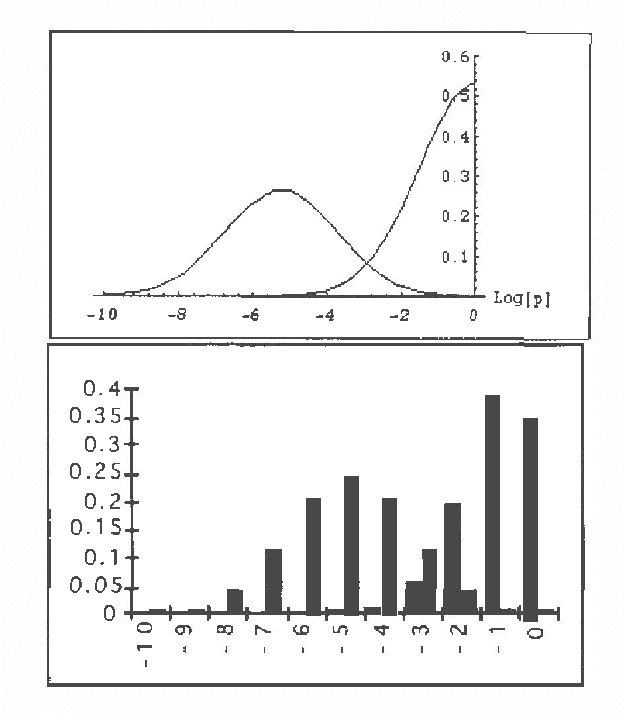
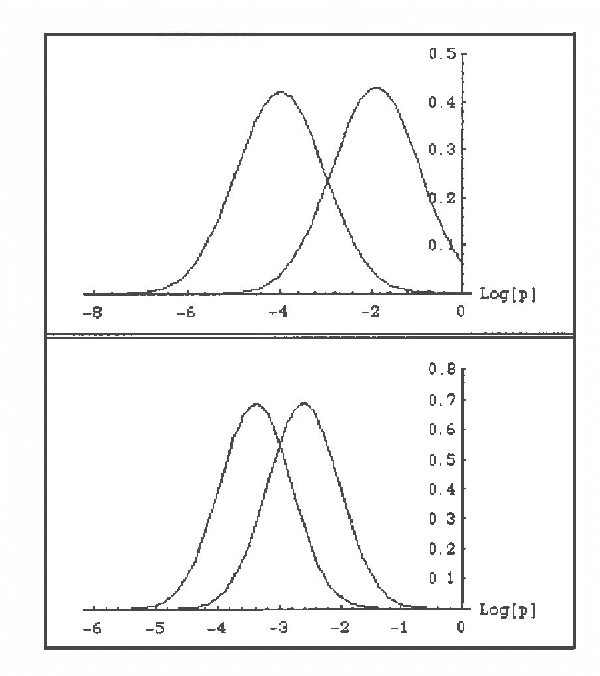
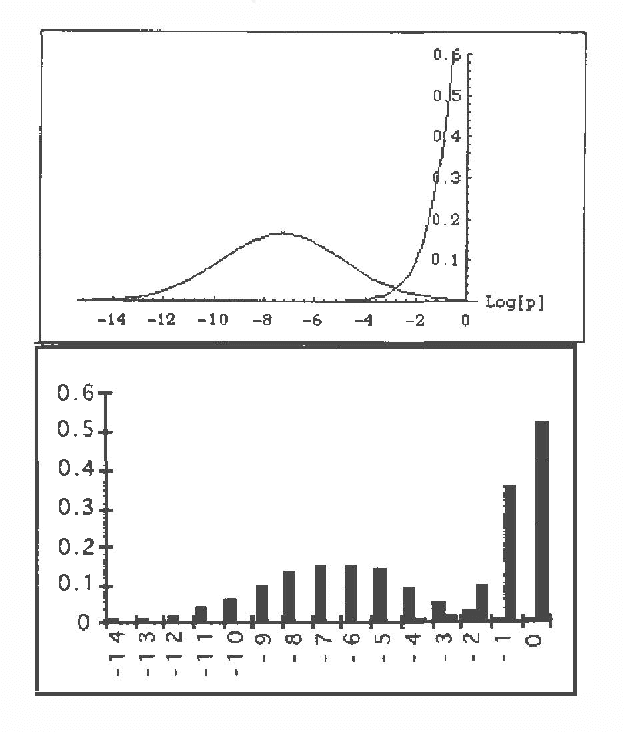
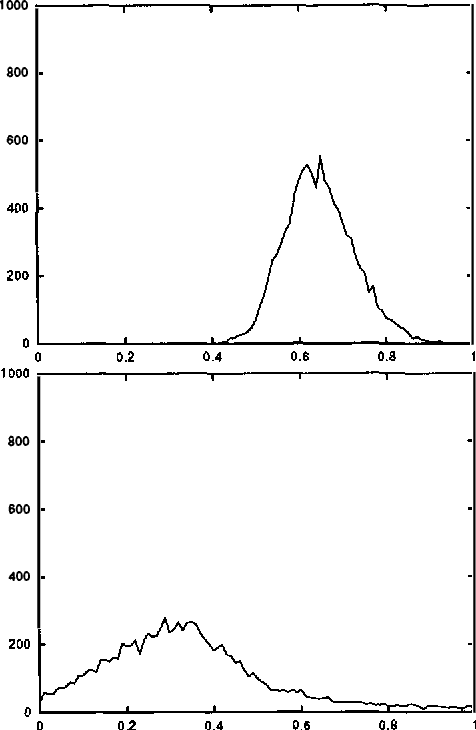
Abstract:Several Artificial Intelligence schemes for reasoning under uncertainty explore either explicitly or implicitly asymmetries among probabilities of various states of their uncertain domain models. Even though the correct working of these schemes is practically contingent upon the existence of a small number of probable states, no formal justification has been proposed of why this should be the case. This paper attempts to fill this apparent gap by studying asymmetries among probabilities of various states of uncertain models. By rewriting the joint probability distribution over a model's variables into a product of individual variables' prior and conditional probability distributions, and applying central limit theorem to this product, we can demonstrate that the probabilities of individual states of the model can be expected to be drawn from highly skewed, log-normal distributions. With sufficient asymmetry in individual prior and conditional probability distributions, a small fraction of states can be expected to cover a large portion of the total probability space with the remaining states having practically negligible probability. Theoretical discussion is supplemented by simulation results and an illustrative real-world example.
Elicitation of Probabilities for Belief Networks: Combining Qualitative and Quantitative Information
Feb 20, 2013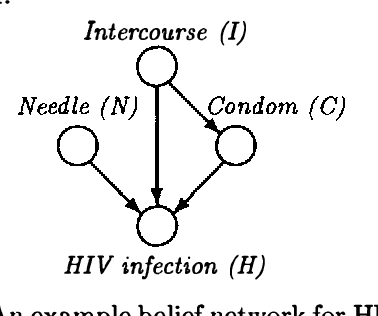
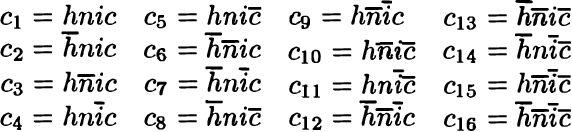
Abstract:Although the usefulness of belief networks for reasoning under uncertainty is widely accepted, obtaining numerical probabilities that they require is still perceived a major obstacle. Often not enough statistical data is available to allow for reliable probability estimation. Available information may not be directly amenable for encoding in the network. Finally, domain experts may be reluctant to provide numerical probabilities. In this paper, we propose a method for elicitation of probabilities from a domain expert that is non-invasive and accommodates whatever probabilistic information the expert is willing to state. We express all available information, whether qualitative or quantitative in nature, in a canonical form consisting of (in) equalities expressing constraints on the hyperspace of possible joint probability distributions. We then use this canonical form to derive second-order probability distributions over the desired probabilities.
Computational Advantages of Relevance Reasoning in Bayesian Belief Networks
Feb 06, 2013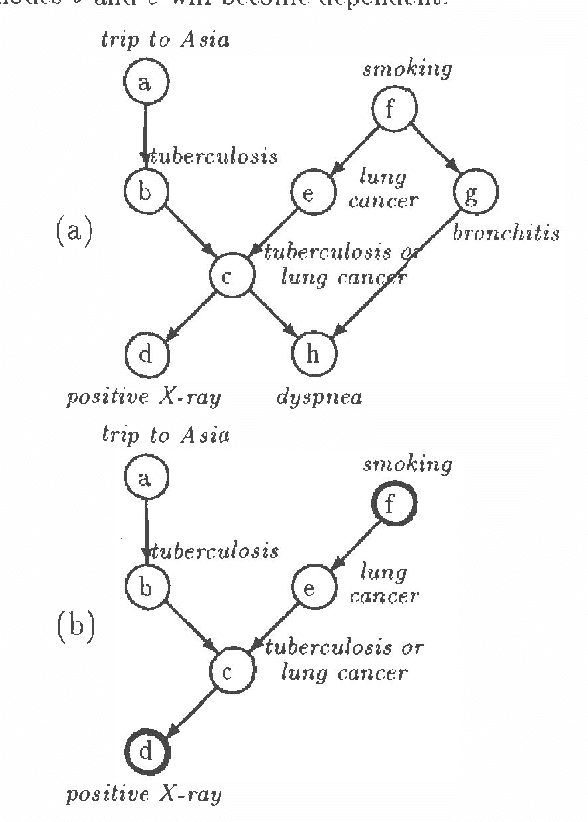
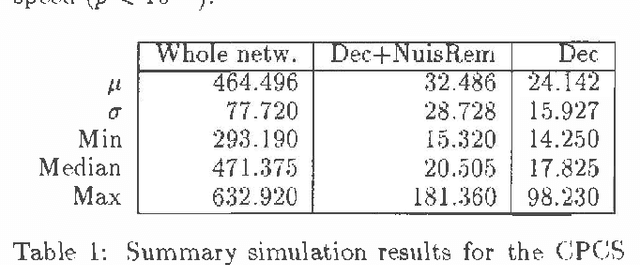


Abstract:This paper introduces a computational framework for reasoning in Bayesian belief networks that derives significant advantages from focused inference and relevance reasoning. This framework is based on d -separation and other simple and computationally efficient techniques for pruning irrelevant parts of a network. Our main contribution is a technique that we call relevance-based decomposition. Relevance-based decomposition approaches belief updating in large networks by focusing on their parts and decomposing them into partially overlapping subnetworks. This makes reasoning in some intractable networks possible and, in addition, often results in significant speedup, as the total time taken to update all subnetworks is in practice often considerably less than the time taken to update the network as a whole. We report results of empirical tests that demonstrate practical significance of our approach.
A Hybrid Anytime Algorithm for the Constructiion of Causal Models From Sparse Data
Jan 23, 2013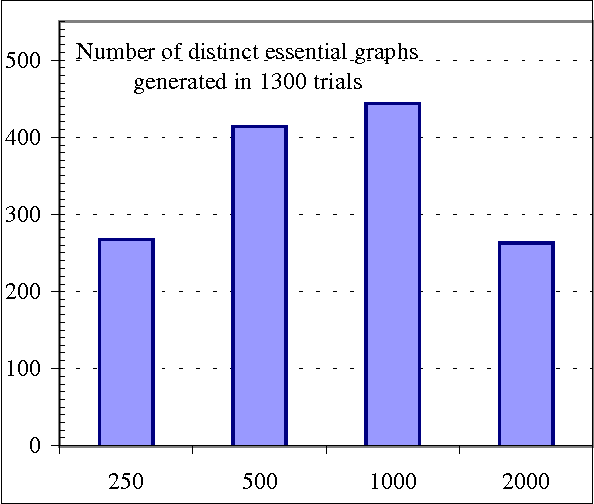
Abstract:We present a hybrid constraint-based/Bayesian algorithm for learning causal networks in the presence of sparse data. The algorithm searches the space of equivalence classes of models (essential graphs) using a heuristic based on conventional constraint-based techniques. Each essential graph is then converted into a directed acyclic graph and scored using a Bayesian scoring metric. Two variants of the algorithm are developed and tested using data from randomly generated networks of sizes from 15 to 45 nodes with data sizes ranging from 250 to 2000 records. Both variations are compared to, and found to consistently outperform two variations of greedy search with restarts.
User Interface Tools for Navigation in Conditional Probability Tables and Elicitation of Probabilities in Bayesian Networks
Jan 18, 2013

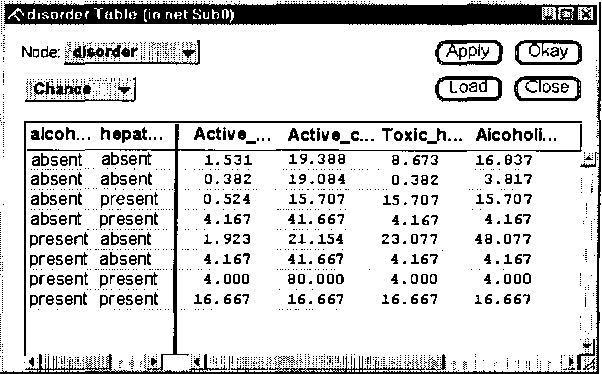
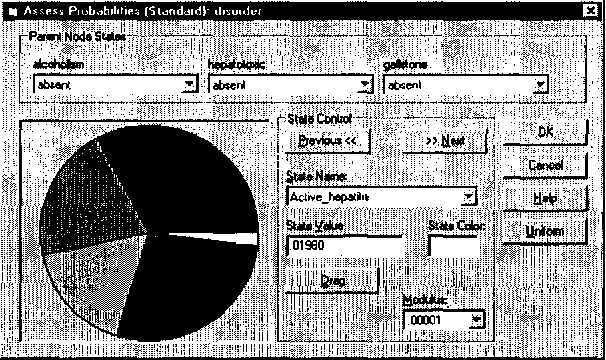
Abstract:Elicitation of probabilities is one of the most laborious tasks in building decision-theoretic models, and one that has so far received only moderate attention in decision-theoretic systems. We propose a set of user interface tools for graphical probabilistic models, focusing on two aspects of probability elicitation: (1) navigation through conditional probability tables and (2) interactive graphical assessment of discrete probability distributions. We propose two new graphical views that aid navigation in very large conditional probability tables: the CPTree (Conditional Probability Tree) and the SCPT (shrinkable Conditional Probability Table). Based on what is known about graphical presentation of quantitative data to humans, we offer several useful enhancements to probability wheel and bar graph, including different chart styles and options that can be adapted to user preferences and needs. We present the results of a simple usability study that proves the value of the proposed tools.
Causal Mechanism-based Model Construction
Jan 16, 2013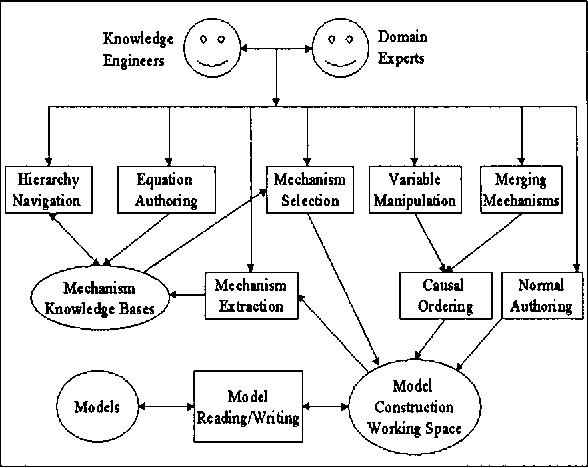

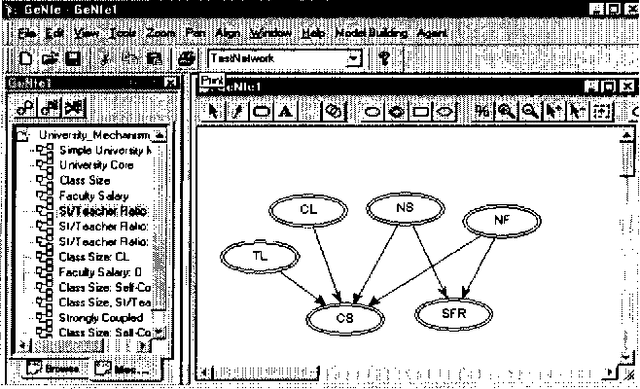
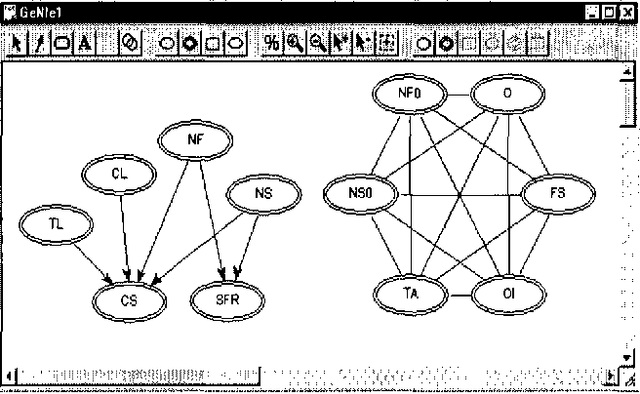
Abstract:We propose a framework for building graphical causal model that is based on the concept of causal mechanisms. Causal models are intuitive for human users and, more importantly, support the prediction of the effect of manipulation. We describe an implementation of the proposed framework as an interactive model construction module, ImaGeNIe, in SMILE (Structural Modeling, Inference, and Learning Engine) and in GeNIe (SMILE's Windows user interface).
Computational Investigation of Low-Discrepancy Sequences in Simulation Algorithms for Bayesian Networks
Jan 16, 2013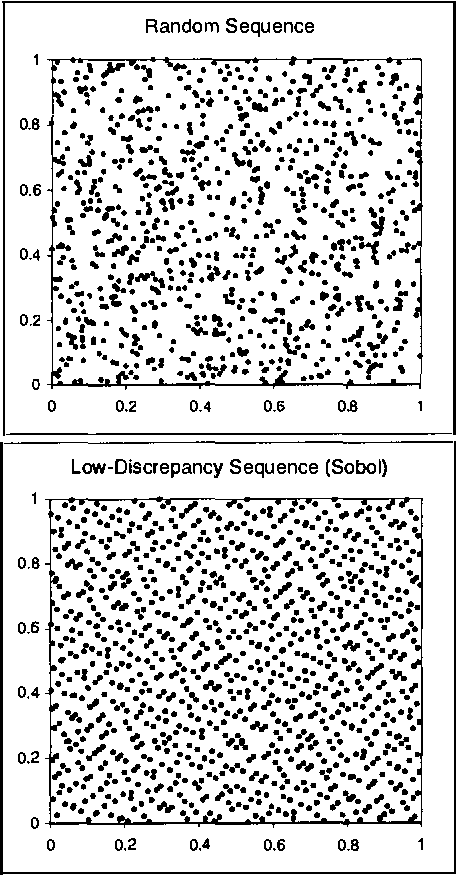
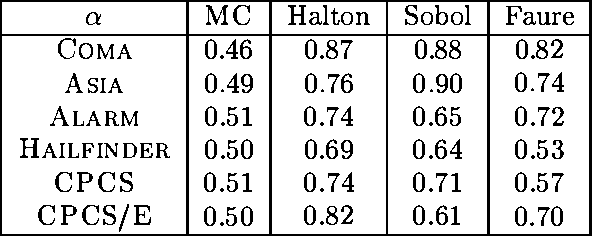

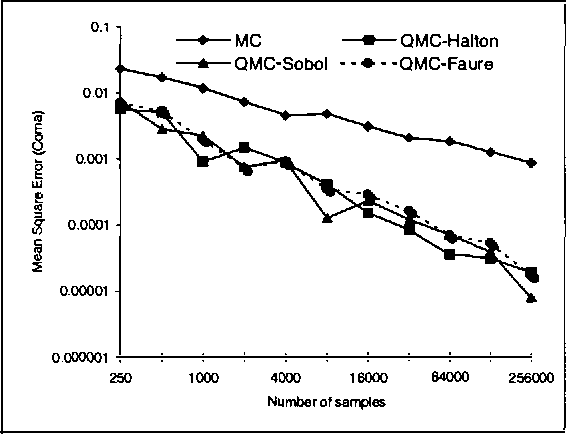
Abstract:Monte Carlo sampling has become a major vehicle for approximate inference in Bayesian networks. In this paper, we investigate a family of related simulation approaches, known collectively as quasi-Monte Carlo methods based on deterministic low-discrepancy sequences. We first outline several theoretical aspects of deterministic low-discrepancy sequences, show three examples of such sequences, and then discuss practical issues related to applying them to belief updating in Bayesian networks. We propose an algorithm for selecting direction numbers for Sobol sequence. Our experimental results show that low-discrepancy sequences (especially Sobol sequence) significantly improve the performance of simulation algorithms in Bayesian networks compared to Monte Carlo sampling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge