Denver Dash
SceneCAD: Predicting Object Alignments and Layouts in RGB-D Scans
Mar 27, 2020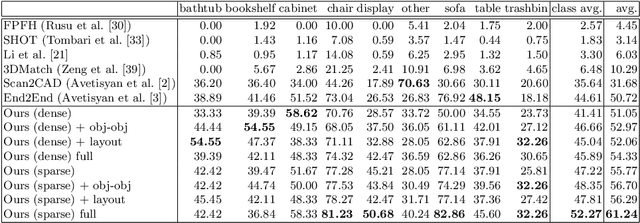
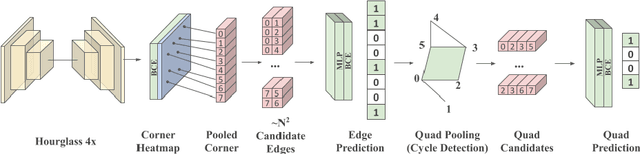
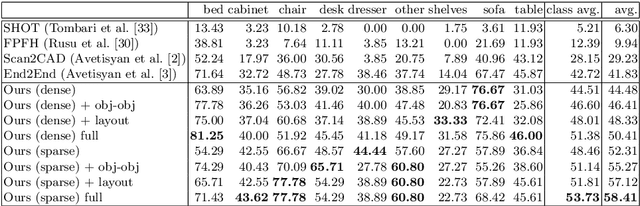
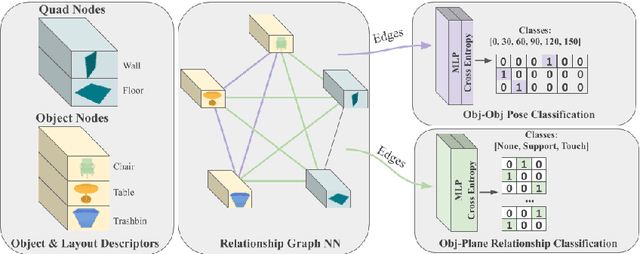
Abstract:We present a novel approach to reconstructing lightweight, CAD-based representations of scanned 3D environments from commodity RGB-D sensors. Our key idea is to jointly optimize for both CAD model alignments as well as layout estimations of the scanned scene, explicitly modeling inter-relationships between objects-to-objects and objects-to-layout. Since object arrangement and scene layout are intrinsically coupled, we show that treating the problem jointly significantly helps to produce globally-consistent representations of a scene. Object CAD models are aligned to the scene by establishing dense correspondences between geometry, and we introduce a hierarchical layout prediction approach to estimate layout planes from corners and edges of the scene.To this end, we propose a message-passing graph neural network to model the inter-relationships between objects and layout, guiding generation of a globally object alignment in a scene. By considering the global scene layout, we achieve significantly improved CAD alignments compared to state-of-the-art methods, improving from 41.83% to 58.41% alignment accuracy on SUNCG and from 50.05% to 61.24% on ScanNet, respectively. The resulting CAD-based representations makes our method well-suited for applications in content creation such as augmented- or virtual reality.
A Hybrid Anytime Algorithm for the Constructiion of Causal Models From Sparse Data
Jan 23, 2013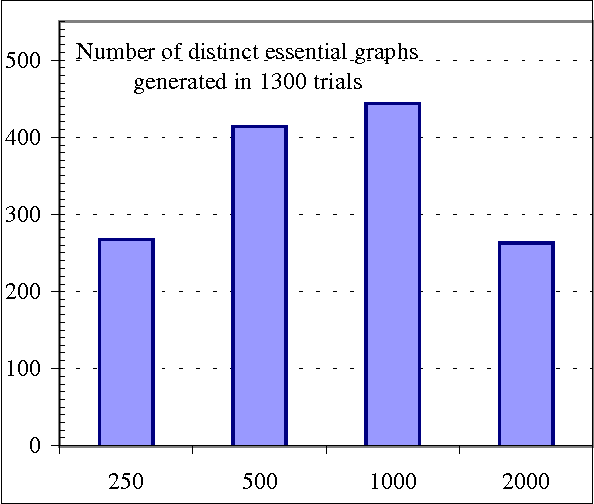
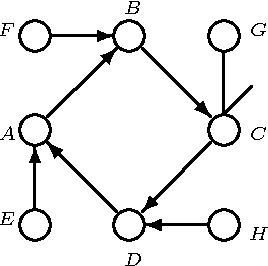
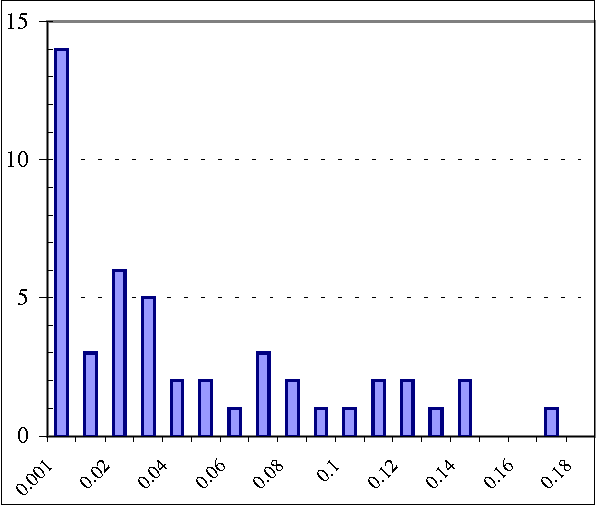
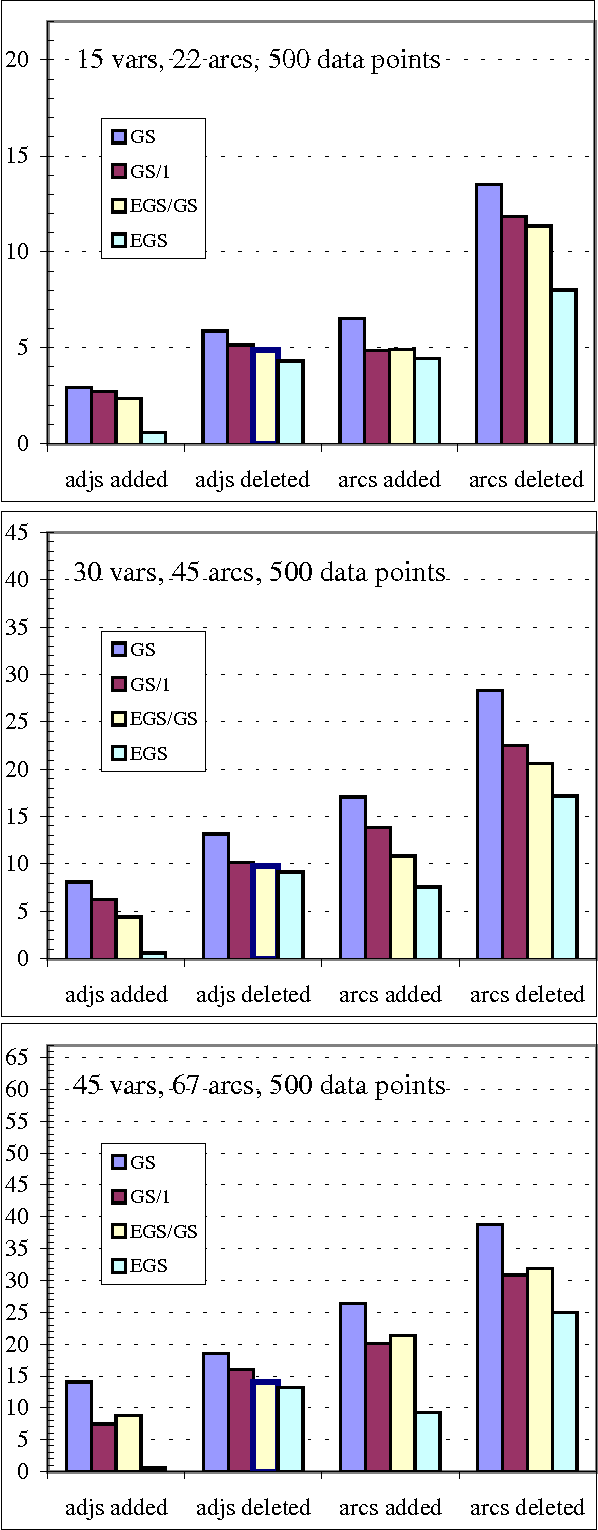
Abstract:We present a hybrid constraint-based/Bayesian algorithm for learning causal networks in the presence of sparse data. The algorithm searches the space of equivalence classes of models (essential graphs) using a heuristic based on conventional constraint-based techniques. Each essential graph is then converted into a directed acyclic graph and scored using a Bayesian scoring metric. Two variants of the algorithm are developed and tested using data from randomly generated networks of sizes from 15 to 45 nodes with data sizes ranging from 250 to 2000 records. Both variations are compared to, and found to consistently outperform two variations of greedy search with restarts.
A Robust Independence Test for Constraint-Based Learning of Causal Structure
Oct 19, 2012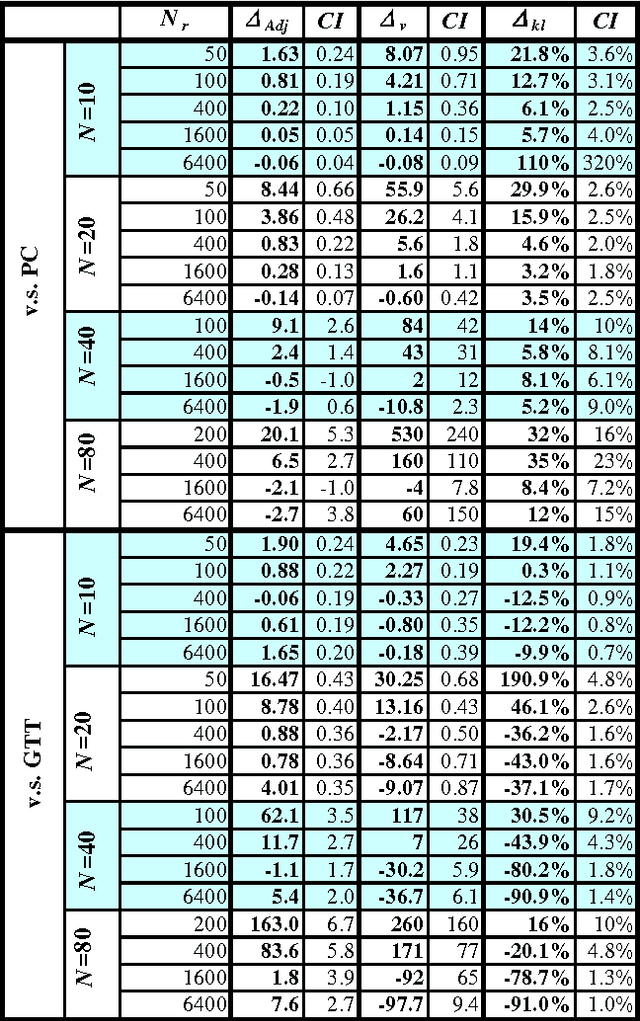
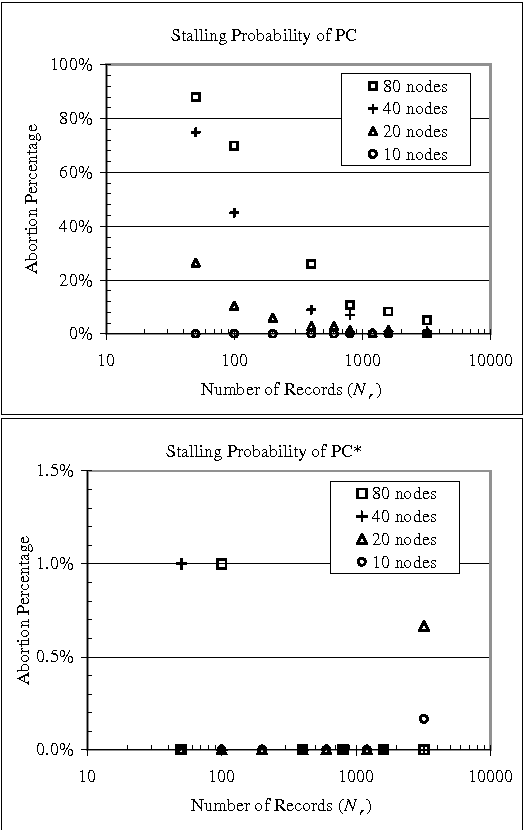
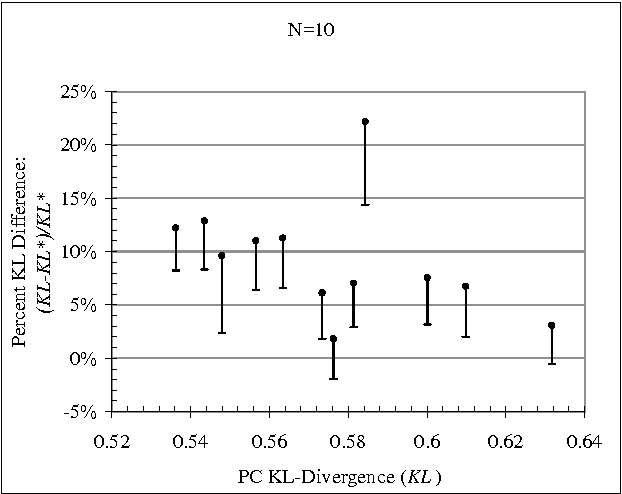
Abstract:Constraint-based (CB) learning is a formalism for learning a causal network with a database D by performing a series of conditional-independence tests to infer structural information. This paper considers a new test of independence that combines ideas from Bayesian learning, Bayesian network inference, and classical hypothesis testing to produce a more reliable and robust test. The new test can be calculated in the same asymptotic time and space required for the standard tests such as the chi-squared test, but it allows the specification of a prior distribution over parameters and can be used when the database is incomplete. We prove that the test is correct, and we demonstrate empirically that, when used with a CB causal discovery algorithm with noninformative priors, it recovers structural features more reliably and it produces networks with smaller KL-Divergence, especially as the number of nodes increases or the number of records decreases. Another benefit is the dramatic reduction in the probability that a CB algorithm will stall during the search, providing a remedy for an annoying problem plaguing CB learning when the database is small.
Bayesian Biosurveillance of Disease Outbreaks
Jul 11, 2012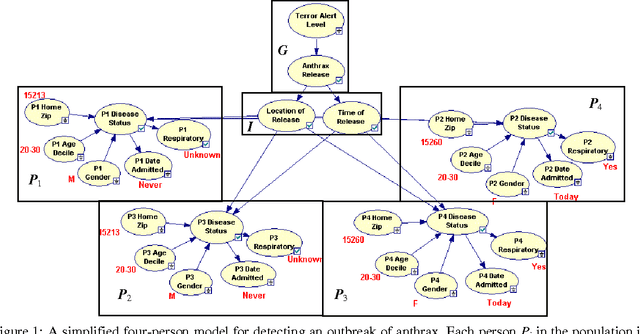
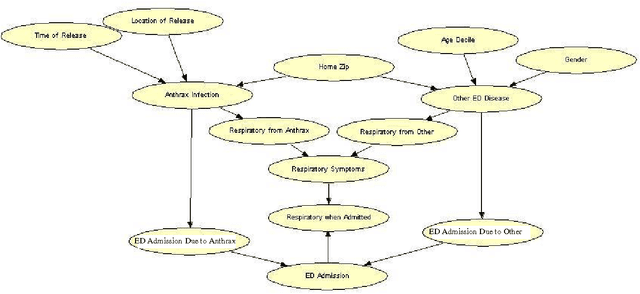
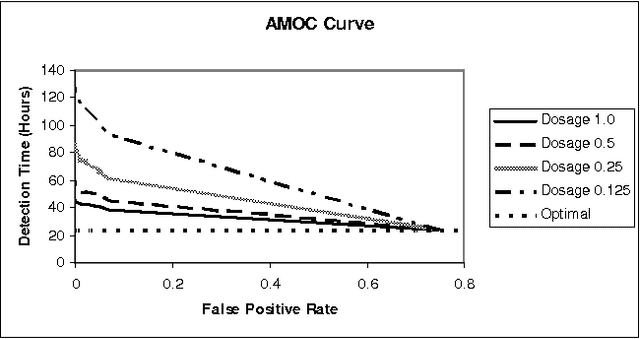
Abstract:Early, reliable detection of disease outbreaks is a critical problem today. This paper reports an investigation of the use of causal Bayesian networks to model spatio-temporal patterns of a non-contagious disease (respiratory anthrax infection) in a population of people. The number of parameters in such a network can become enormous, if not carefully managed. Also, inference needs to be performed in real time as population data stream in. We describe techniques we have applied to address both the modeling and inference challenges. A key contribution of this paper is the explication of assumptions and techniques that are sufficient to allow the scaling of Bayesian network modeling and inference to millions of nodes for real-time surveillance applications. The results reported here provide a proof-of-concept that Bayesian networks can serve as the foundation of a system that effectively performs Bayesian biosurveillance of disease outbreaks.
Efficient inference in persistent Dynamic Bayesian Networks
Jun 13, 2012
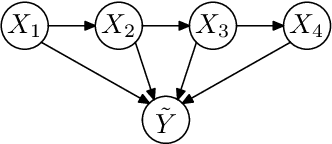
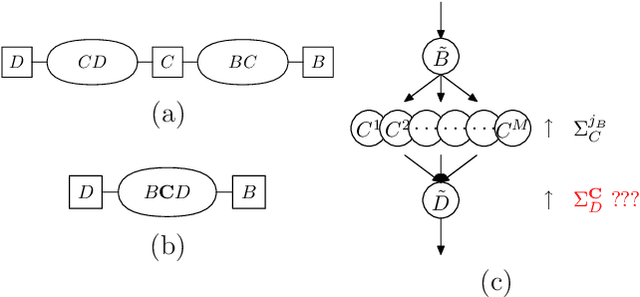
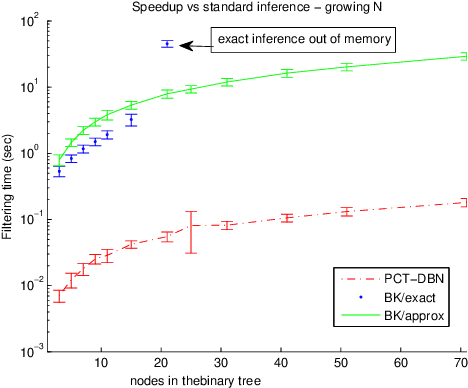
Abstract:Numerous temporal inference tasks such as fault monitoring and anomaly detection exhibit a persistence property: for example, if something breaks, it stays broken until an intervention. When modeled as a Dynamic Bayesian Network, persistence adds dependencies between adjacent time slices, often making exact inference over time intractable using standard inference algorithms. However, we show that persistence implies a regular structure that can be exploited for efficient inference. We present three successively more general classes of models: persistent causal chains (PCCs), persistent causal trees (PCTs) and persistent polytrees (PPTs), and the corresponding exact inference algorithms that exploit persistence. We show that analytic asymptotic bounds for our algorithms compare favorably to junction tree inference; and we demonstrate empirically that we can perform exact smoothing on the order of 100 times faster than the approximate Boyen-Koller method on randomly generated instances of persistent tree models. We also show how to handle non-persistent variables and how persistence can be exploited effectively for approximate filtering.
Learning Why Things Change: The Difference-Based Causality Learner
Mar 15, 2012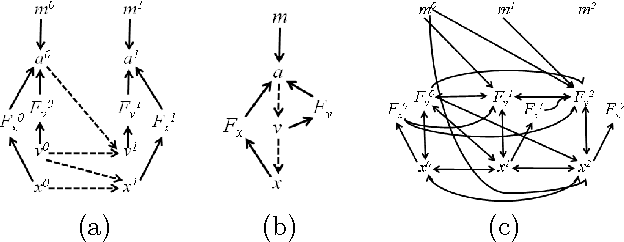
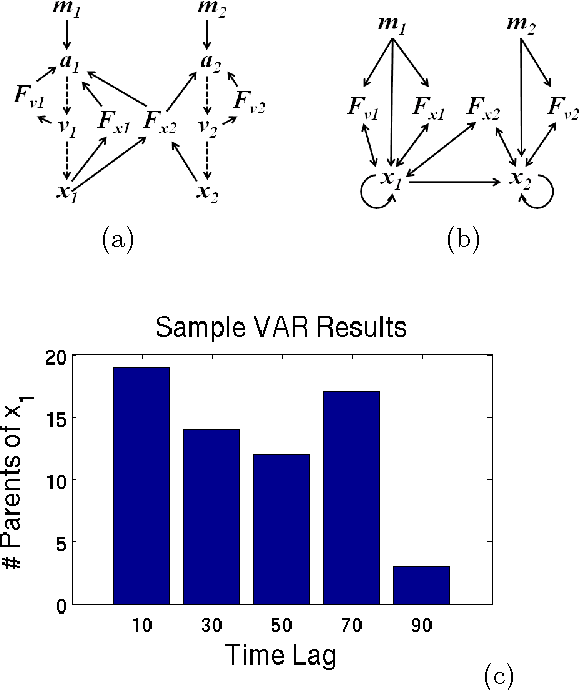
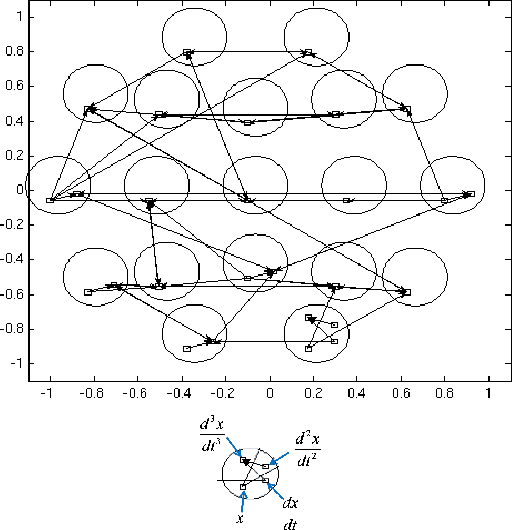
Abstract:In this paper, we present the Difference- Based Causality Learner (DBCL), an algorithm for learning a class of discrete-time dynamic models that represents all causation across time by means of difference equations driving change in a system. We motivate this representation with real-world mechanical systems and prove DBCL's correctness for learning structure from time series data, an endeavour that is complicated by the existence of latent derivatives that have to be detected. We also prove that, under common assumptions for causal discovery, DBCL will identify the presence or absence of feedback loops, making the model more useful for predicting the effects of manipulating variables when the system is in equilibrium. We argue analytically and show empirically the advantages of DBCL over vector autoregression (VAR) and Granger causality models as well as modified forms of Bayesian and constraintbased structure discovery algorithms. Finally, we show that our algorithm can discover causal directions of alpha rhythms in human brains from EEG data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge