A Robust Independence Test for Constraint-Based Learning of Causal Structure
Paper and Code
Oct 19, 2012
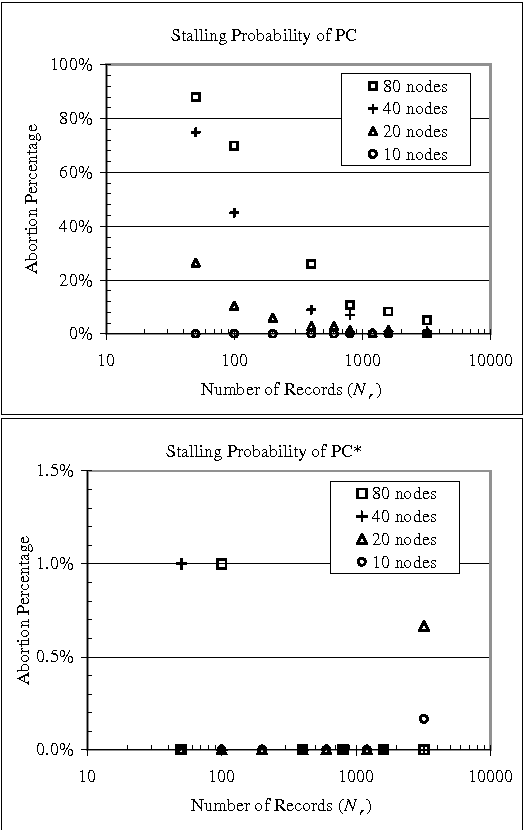
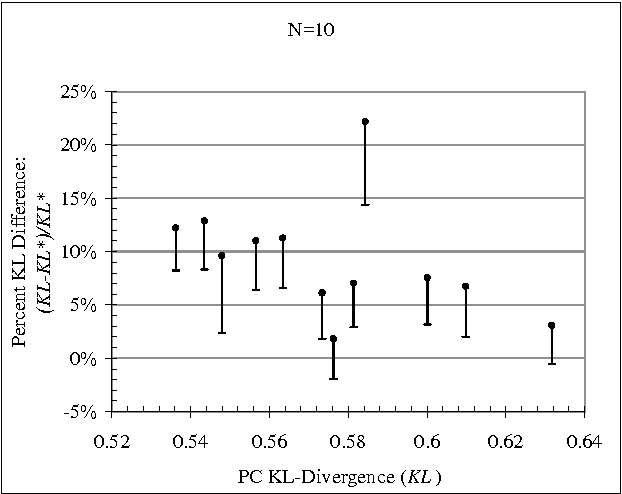
Constraint-based (CB) learning is a formalism for learning a causal network with a database D by performing a series of conditional-independence tests to infer structural information. This paper considers a new test of independence that combines ideas from Bayesian learning, Bayesian network inference, and classical hypothesis testing to produce a more reliable and robust test. The new test can be calculated in the same asymptotic time and space required for the standard tests such as the chi-squared test, but it allows the specification of a prior distribution over parameters and can be used when the database is incomplete. We prove that the test is correct, and we demonstrate empirically that, when used with a CB causal discovery algorithm with noninformative priors, it recovers structural features more reliably and it produces networks with smaller KL-Divergence, especially as the number of nodes increases or the number of records decreases. Another benefit is the dramatic reduction in the probability that a CB algorithm will stall during the search, providing a remedy for an annoying problem plaguing CB learning when the database is small.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge