Monte-Carlo optimizations for resource allocation problems in stochastic network systems

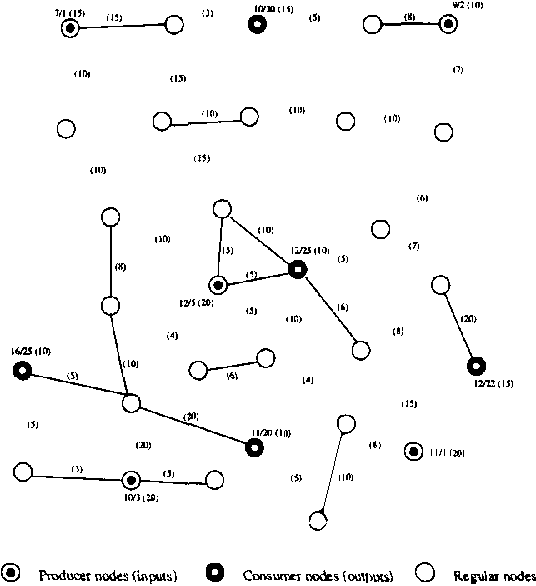
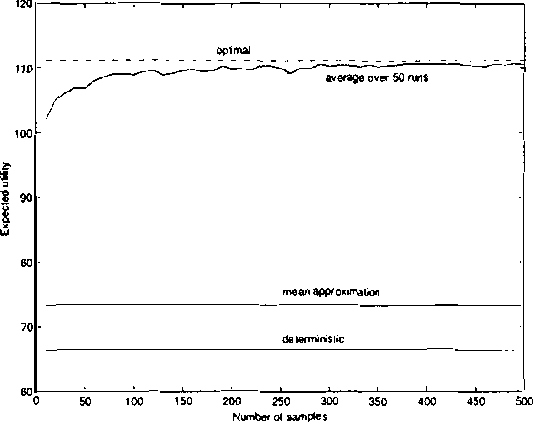
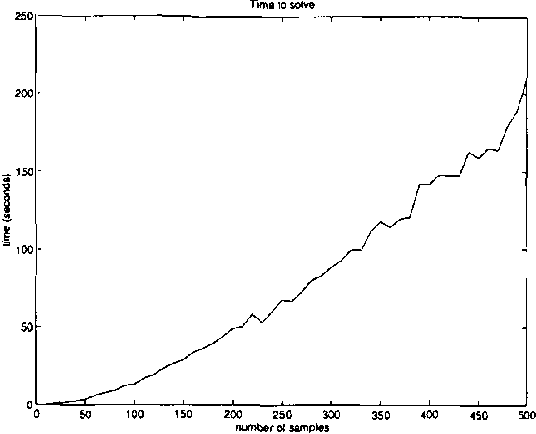
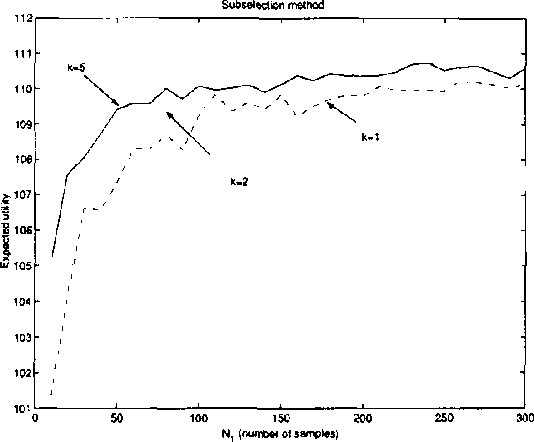
Real-world distributed systems and networks are often unreliable and subject to random failures of its components. Such a stochastic behavior affects adversely the complexity of optimization tasks performed routinely upon such systems, in particular, various resource allocation tasks. In this work we investigate and develop Monte Carlo solutions for a class of two-stage optimization problems in stochastic networks in which the expected value of resource allocations before and after stochastic failures needs to be optimized. The limitation of these problems is that their exact solutions are exponential in the number of unreliable network components: thus, exact methods do not scale-up well to large networks often seen in practice. We first prove that Monte Carlo optimization methods can overcome the exponential bottleneck of exact methods. Next we support our theoretical findings on resource allocation experiments and show a very good scale-up potential of the new methods to large stochastic networks.

Efficient inference in persistent Dynamic Bayesian Networks

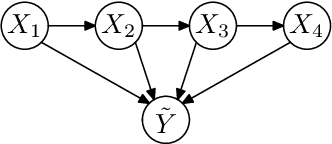
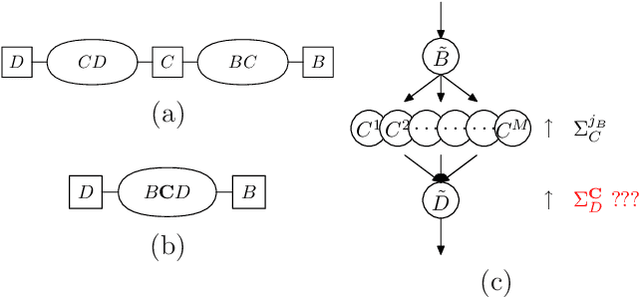
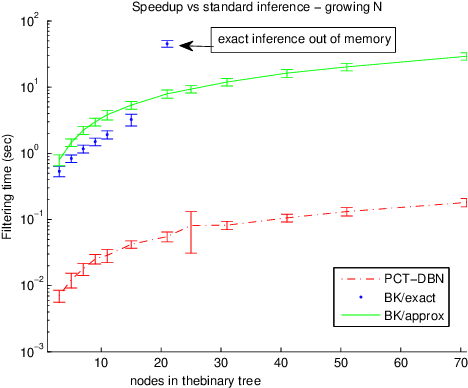
Numerous temporal inference tasks such as fault monitoring and anomaly detection exhibit a persistence property: for example, if something breaks, it stays broken until an intervention. When modeled as a Dynamic Bayesian Network, persistence adds dependencies between adjacent time slices, often making exact inference over time intractable using standard inference algorithms. However, we show that persistence implies a regular structure that can be exploited for efficient inference. We present three successively more general classes of models: persistent causal chains (PCCs), persistent causal trees (PCTs) and persistent polytrees (PPTs), and the corresponding exact inference algorithms that exploit persistence. We show that analytic asymptotic bounds for our algorithms compare favorably to junction tree inference; and we demonstrate empirically that we can perform exact smoothing on the order of 100 times faster than the approximate Boyen-Koller method on randomly generated instances of persistent tree models. We also show how to handle non-persistent variables and how persistence can be exploited effectively for approximate filtering.