Efficient inference in persistent Dynamic Bayesian Networks

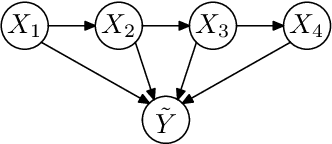
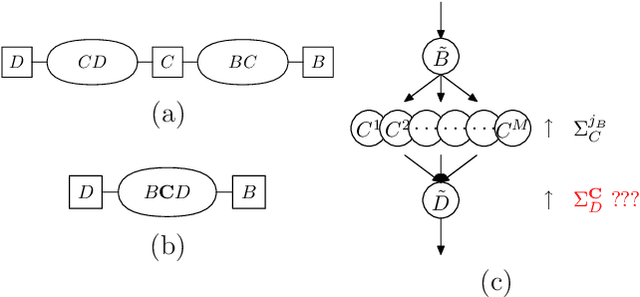
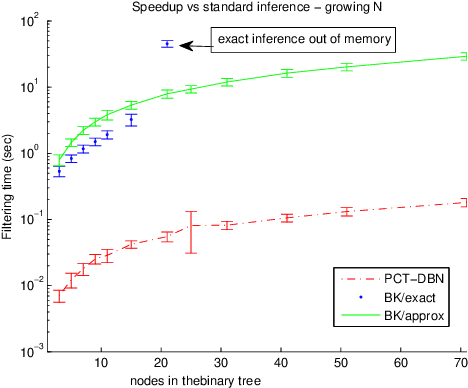
Numerous temporal inference tasks such as fault monitoring and anomaly detection exhibit a persistence property: for example, if something breaks, it stays broken until an intervention. When modeled as a Dynamic Bayesian Network, persistence adds dependencies between adjacent time slices, often making exact inference over time intractable using standard inference algorithms. However, we show that persistence implies a regular structure that can be exploited for efficient inference. We present three successively more general classes of models: persistent causal chains (PCCs), persistent causal trees (PCTs) and persistent polytrees (PPTs), and the corresponding exact inference algorithms that exploit persistence. We show that analytic asymptotic bounds for our algorithms compare favorably to junction tree inference; and we demonstrate empirically that we can perform exact smoothing on the order of 100 times faster than the approximate Boyen-Koller method on randomly generated instances of persistent tree models. We also show how to handle non-persistent variables and how persistence can be exploited effectively for approximate filtering.