Monte-Carlo optimizations for resource allocation problems in stochastic network systems
Paper and Code
Oct 19, 2012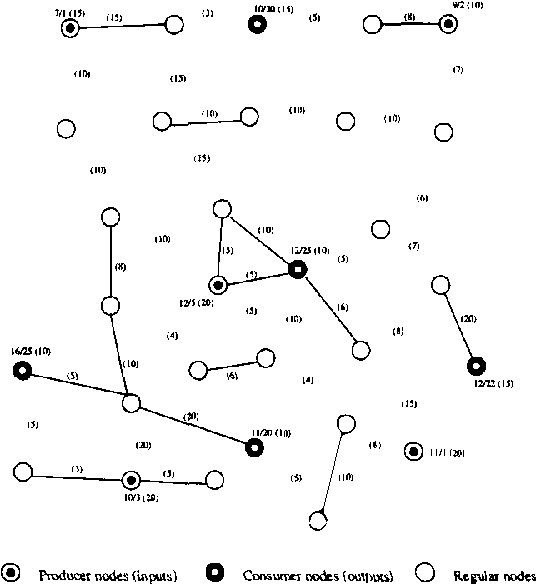
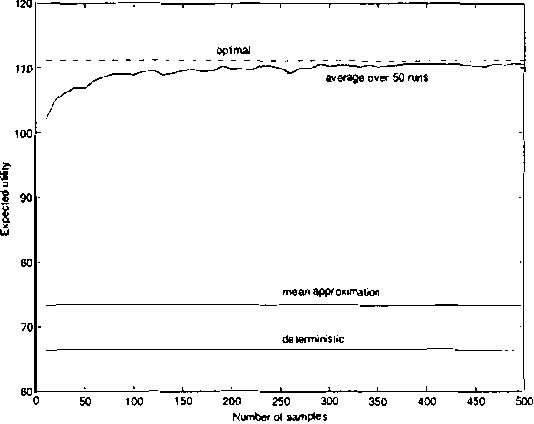
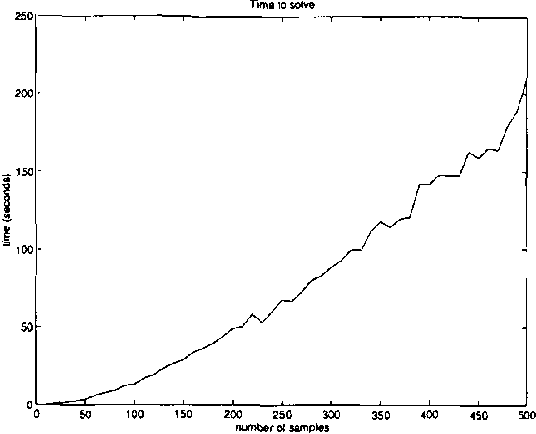
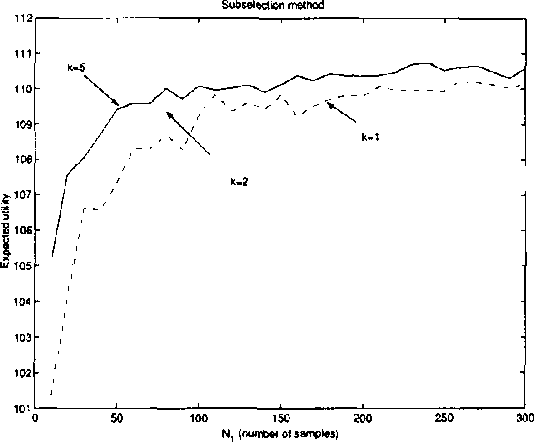
Real-world distributed systems and networks are often unreliable and subject to random failures of its components. Such a stochastic behavior affects adversely the complexity of optimization tasks performed routinely upon such systems, in particular, various resource allocation tasks. In this work we investigate and develop Monte Carlo solutions for a class of two-stage optimization problems in stochastic networks in which the expected value of resource allocations before and after stochastic failures needs to be optimized. The limitation of these problems is that their exact solutions are exponential in the number of unreliable network components: thus, exact methods do not scale-up well to large networks often seen in practice. We first prove that Monte Carlo optimization methods can overcome the exponential bottleneck of exact methods. Next we support our theoretical findings on resource allocation experiments and show a very good scale-up potential of the new methods to large stochastic networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge