Computational Investigation of Low-Discrepancy Sequences in Simulation Algorithms for Bayesian Networks

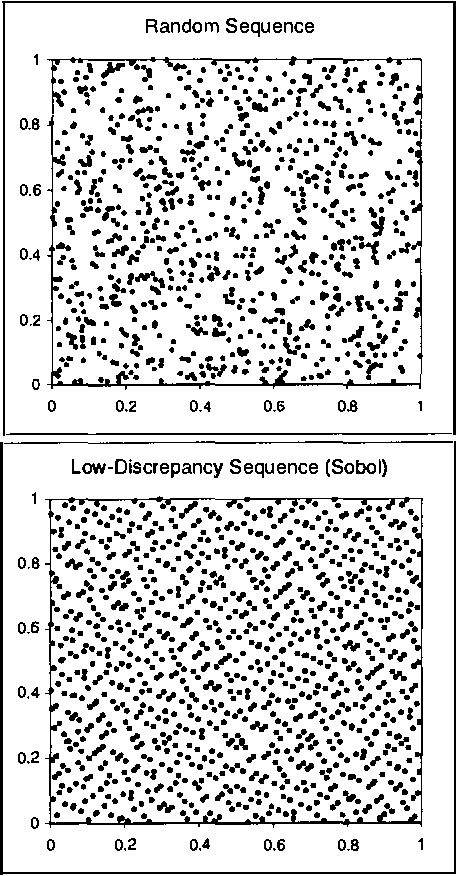
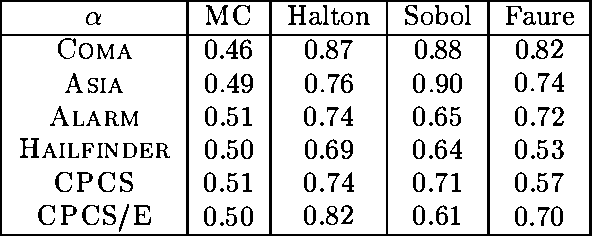
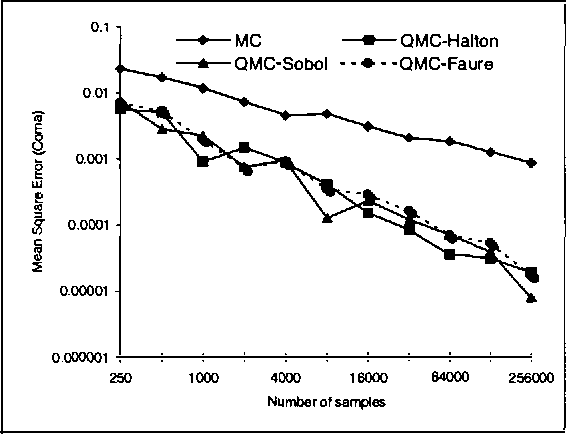
Monte Carlo sampling has become a major vehicle for approximate inference in Bayesian networks. In this paper, we investigate a family of related simulation approaches, known collectively as quasi-Monte Carlo methods based on deterministic low-discrepancy sequences. We first outline several theoretical aspects of deterministic low-discrepancy sequences, show three examples of such sequences, and then discuss practical issues related to applying them to belief updating in Bayesian networks. We propose an algorithm for selecting direction numbers for Sobol sequence. Our experimental results show that low-discrepancy sequences (especially Sobol sequence) significantly improve the performance of simulation algorithms in Bayesian networks compared to Monte Carlo sampling.