How Does Bayesian Causal Discovery Fail? Characterising Structural Consequences in Linear Gaussian Networks under Latent Confounding

Bayesian causal discovery is widely used for its ability to quantify epistemic uncertainty over directed acyclic graphs (DAGs) through posterior inference. However, its behaviour under latent confounding remains poorly understood, as existing work typically notes that confounding breaks identifiability without characterising how the posterior distribution over DAGs responds. In this work, we analyse posterior behaviour under latent confounding in linear Gaussian causal models, focusing on additive latent confounding between exactly two observed variables. We derive a critical correlation threshold above which the score function favours graphs with a spurious edge between the confounded variables, and show that this threshold decreases with sample size -- more data lowers the correlation required for the spurious edge to be favoured. Beyond this threshold, we characterize two distinct posterior failure regimes determined by the local structure around the confounded variables. Our findings are supported by exact posterior computations on multiple graph structures, demonstrating both the predicted failure regimes.

Parameterized Argumentation-based Reasoning Tasks for Benchmarking Generative Language Models

Generative large language models as tools in the legal domain have the potential to improve the justice system. However, the reasoning behavior of current generative models is brittle and poorly understood, hence cannot be responsibly applied in the domains of law and evidence. In this paper, we introduce an approach for creating benchmarks that can be used to evaluate the reasoning capabilities of generative language models. These benchmarks are dynamically varied, scalable in their complexity, and have formally unambiguous interpretations. In this study, we illustrate the approach on the basis of witness testimony, focusing on the underlying argument attack structure. We dynamically generate both linear and non-linear argument attack graphs of varying complexity and translate these into reasoning puzzles about witness testimony expressed in natural language. We show that state-of-the-art large language models often fail in these reasoning puzzles, already at low complexity. Obvious mistakes are made by the models, and their inconsistent performance indicates that their reasoning capabilities are brittle. Furthermore, at higher complexity, even state-of-the-art models specifically presented for reasoning capabilities make mistakes. We show the viability of using a parametrized benchmark with varying complexity to evaluate the reasoning capabilities of generative language models. As such, the findings contribute to a better understanding of the limitations of the reasoning capabilities of generative models, which is essential when designing responsible AI systems in the legal domain.

Discovering the Rationale of Decisions: Experiments on Aligning Learning and Reasoning

In AI and law, systems that are designed for decision support should be explainable when pursuing justice. In order for these systems to be fair and responsible, they should make correct decisions and make them using a sound and transparent rationale. In this paper, we introduce a knowledge-driven method for model-agnostic rationale evaluation using dedicated test cases, similar to unit-testing in professional software development. We apply this new method in a set of machine learning experiments aimed at extracting known knowledge structures from artificial datasets from fictional and non-fictional legal settings. We show that our method allows us to analyze the rationale of black-box machine learning systems by assessing which rationale elements are learned or not. Furthermore, we show that the rationale can be adjusted using tailor-made training data based on the results of the rationale evaluation.

How to Elicit Many Probabilities

In building Bayesian belief networks, the elicitation of all probabilities required can be a major obstacle. We learned the extent of this often-cited observation in the construction of the probabilistic part of a complex influence diagram in the field of cancer treatment. Based upon our negative experiences with existing methods, we designed a new method for probability elicitation from domain experts. The method combines various ideas, among which are the ideas of transcribing probabilities and of using a scale with both numerical and verbal anchors for marking assessments. In the construction of the probabilistic part of our influence diagram, the method proved to allow for the elicitation of many probabilities in little time.

Enhancing QPNs for Trade-off Resolution

Qualitative probabilistic networks have been introduced as qualitative abstractions of Bayesian belief networks. One of the major drawbacks of these qualitative networks is their coarse level of detail, which may lead to unresolved trade-offs during inference. We present an enhanced formalism for qualitative networks with a finer level of detail. An enhanced qualitative probabilistic network differs from a regular qualitative network in that it distinguishes between strong and weak influences. Enhanced qualitative probabilistic networks are purely qualitative in nature, as regular qualitative networks are, yet allow for efficiently resolving trade-offs during inference.

Pivotal Pruning of Trade-offs in QPNs

Qualitative probabilistic networks have been designed for probabilistic reasoning in a qualitative way. Due to their coarse level of representation detail, qualitative probabilistic networks do not provide for resolving trade-offs and typically yield ambiguous results upon inference. We present an algorithm for computing more insightful results for unresolved trade-offs. The algorithm builds upon the idea of using pivots to zoom in on the trade-offs and identifying the information that would serve to resolve them.

Analysing Sensitivity Data from Probabilistic Networks

With the advance of efficient analytical methods for sensitivity analysis ofprobabilistic networks, the interest in the sensitivities revealed by real-life networks is rekindled. As the amount of data resulting from a sensitivity analysis of even a moderately-sized network is alreadyoverwhelming, methods for extracting relevant information are called for. One such methodis to study the derivative of the sensitivity functions yielded for a network's parameters. We further propose to build upon the concept of admissible deviation, that is, the extent to which a parameter can deviate from the true value without inducing a change in the most likely outcome. We illustrate these concepts by means of a sensitivity analysis of a real-life probabilistic network in oncology.

From Qualitative to Quantitative Probabilistic Networks

Quantification is well known to be a major obstacle in the construction of a probabilistic network, especially when relying on human experts for this purpose. The construction of a qualitative probabilistic network has been proposed as an initial step in a network s quantification, since the qualitative network can be used TO gain preliminary insight IN the projected networks reasoning behaviour. We extend on this idea and present a new type of network in which both signs and numbers are specified; we further present an associated algorithm for probabilistic inference. Building upon these semi-qualitative networks, a probabilistic network can be quantified and studied in a stepwise manner. As a result, modelling inadequacies can be detected and amended at an early stage in the quantification process.

Upgrading Ambiguous Signs in QPNs

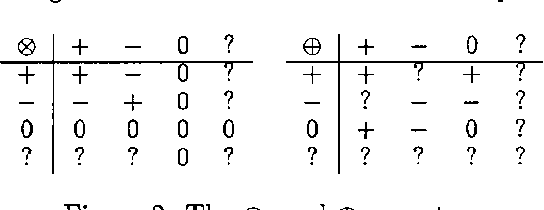
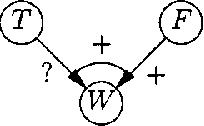
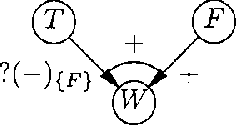
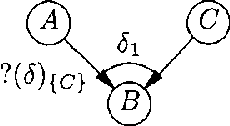
WA qualitative probabilistic network models the probabilistic relationships between its variables by means of signs. Non-monotonic influences have associated an ambiguous sign. These ambiguous signs typically lead to uninformative results upon inference. A non-monotonic influence can, however, be associated with a, more informative, sign that indicates its effect in the current state of the network. To capture this effect, we introduce the concept of situational sign. Furthermore, if the network converts to a state in which all variables that provoke the non-monotonicity have been observed, a non-monotonic influence reduces to a monotonic influence. We study the persistence and propagation of situational signs upon inference and give a method to establish the sign of a reduced influence.

Evidence-invariant Sensitivity Bounds

The sensitivities revealed by a sensitivity analysis of a probabilistic network typically depend on the entered evidence. For a real-life network therefore, the analysis is performed a number of times, with different evidence. Although efficient algorithms for sensitivity analysis exist, a complete analysis is often infeasible because of the large range of possible combinations of observations. In this paper we present a method for studying sensitivities that are invariant to the evidence entered. Our method builds upon the idea of establishing bounds between which a parameter can be varied without ever inducing a change in the most likely value of a variable of interest.