Probabilistic Models with Deep Neural Networks
Paper and Code
Aug 09, 2019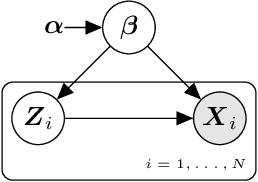
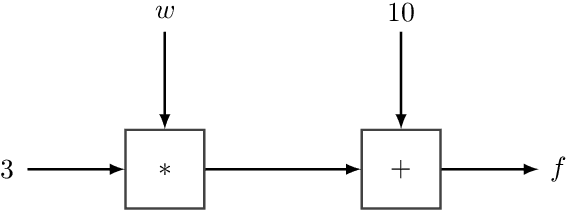
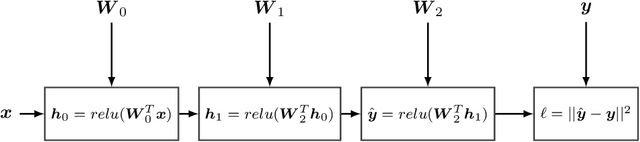
Recent advances in statistical inference have significantly expanded the toolbox of probabilistic modeling. Historically, probabilistic modeling has been constrained to (i) very restricted model classes where exact or approximate probabilistic inference were feasible, and (ii) small or medium-sized data sets which fit within the main memory of the computer. However, developments in variational inference, a general form of approximate probabilistic inference originated in statistical physics, are allowing probabilistic modeling to overcome these restrictions: (i) Approximate probabilistic inference is now possible over a broad class of probabilistic models containing a large number of parameters, and (ii) scalable inference methods based on stochastic gradient descent and distributed computation engines allow to apply probabilistic modeling over massive data sets. One important practical consequence of these advances is the possibility to include deep neural networks within a probabilistic model to capture complex non-linear stochastic relationships between random variables. These advances in conjunction with the release of novel probabilistic modeling toolboxes have greatly expanded the scope of application of probabilistic models, and allow these models to take advantage of the recent strides made by the deep learning community. In this paper we review the main concepts, methods and tools needed to use deep neural networks within a probabilistic modeling framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge