Split-kl and PAC-Bayes-split-kl Inequalities
Paper and Code
Jun 01, 2022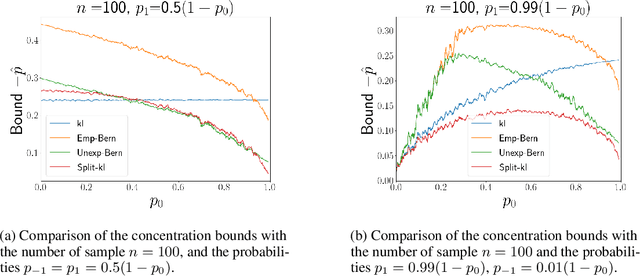

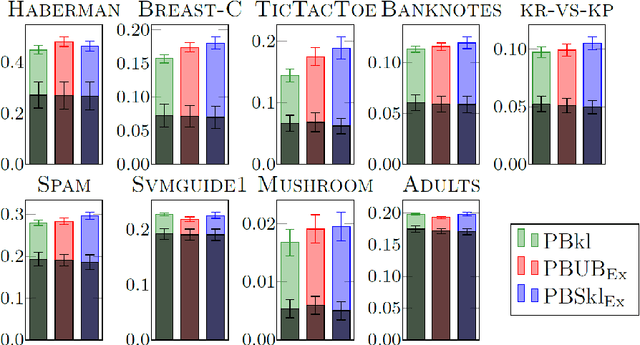
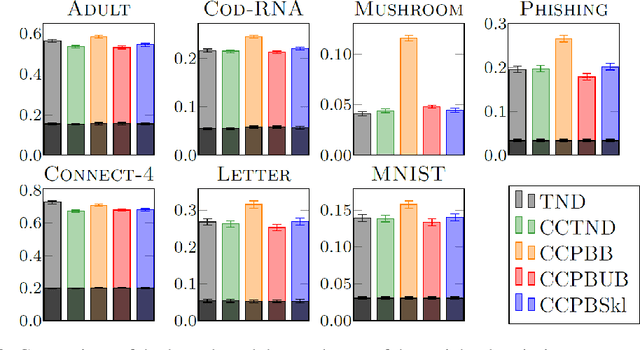
We present a new concentration of measure inequality for sums of independent bounded random variables, which we name a split-kl inequality. The inequality combines the combinatorial power of the kl inequality with ability to exploit low variance. While for Bernoulli random variables the kl inequality is tighter than the Empirical Bernstein, for random variables taking values inside a bounded interval and having low variance the Empirical Bernstein inequality is tighter than the kl. The proposed split-kl inequality yields the best of both worlds. We discuss an application of the split-kl inequality to bounding excess losses. We also derive a PAC-Bayes-split-kl inequality and use a synthetic example and several UCI datasets to compare it with the PAC-Bayes-kl, PAC-Bayes Empirical Bernstein, PAC-Bayes Unexpected Bernstein, and PAC-Bayes Empirical Bennett inequalities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge