EM Based Bounding of Unidentifiable Queries in Structural Causal Models
Paper and Code
Nov 04, 2020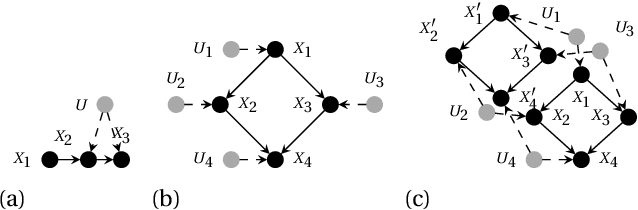
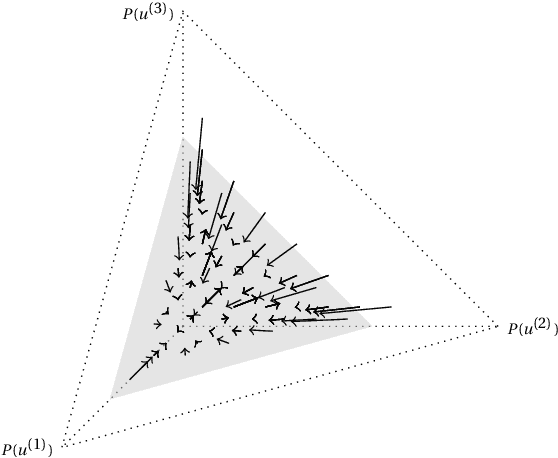
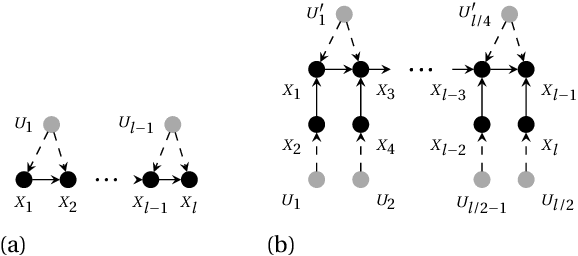
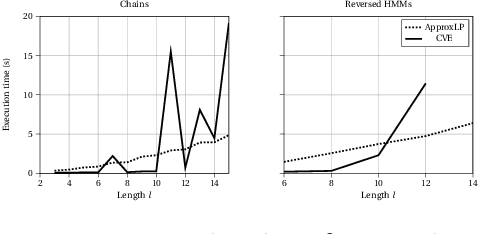
A structural causal model is made of endogenous (manifest) and exogenous (latent) variables. In a recent paper, it has been shown that endogenous observations induce linear constraints on the probabilities of the exogenous variables. This allows to exactly map a causal model into a \emph{credal network}. Causal inferences, such as interventions and counterfactuals, can consequently be obtained by standard credal network algorithms. These natively return sharp values in the identifiable case, while intervals corresponding to the exact bounds are produced for unidentifiable queries. In this paper we present an approximate characterization of the constraints on the exogenous probabilities. This is based on a specialization of the EM algorithm to the treatment of the missing values in the exogenous observations. Multiple EM runs can be consequently used to describe the causal model as a set of Bayesian networks and, hence, a credal network to be queried for the bounding of unidentifiable queries. Preliminary empirical tests show how this approach might provide good inner bounds with relatively few runs. This is a promising direction for causal analysis in models whose topology prevents a straightforward specification of the credal mapping.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge