Nonlinear desirability theory

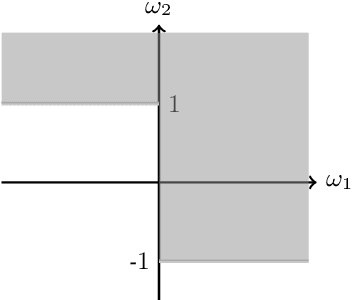
Desirability can be understood as an extension of Anscombe and Aumann's Bayesian decision theory to sets of expected utilities. At the core of desirability lies an assumption of linearity of the scale in which rewards are measured. It is a traditional assumption used to derive the expected utility model, which clashes with a general representation of rational decision making, though. Allais has, in particular, pointed this out in 1953 with his famous paradox. We note that the utility scale plays the role of a closure operator when we regard desirability as a logical theory. This observation enables us to extend desirability to the nonlinear case by letting the utility scale be represented via a general closure operator. The new theory directly expresses rewards in actual nonlinear currency (money), much in Savage's spirit, while arguably weakening the founding assumptions to a minimum. We characterise the main properties of the new theory both from the perspective of sets of gambles and of their lower and upper prices (previsions). We show how Allais paradox finds a solution in the new theory, and discuss the role of sets of probabilities in the theory.

Lexicographic choice functions

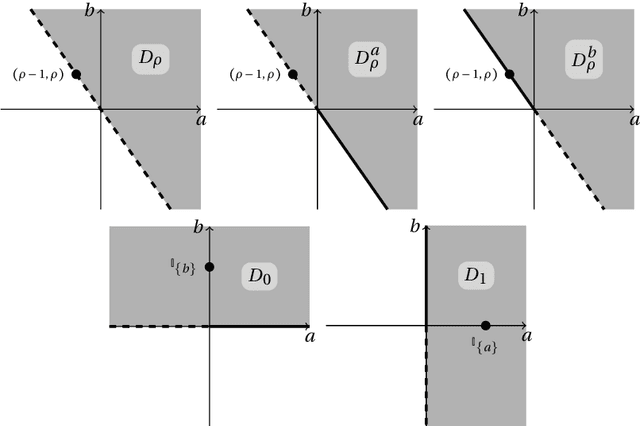
We investigate a generalisation of the coherent choice functions considered by Seidenfeld et al. (2010), by sticking to the convexity axiom but imposing no Archimedeanity condition. We define our choice functions on vector spaces of options, which allows us to incorporate as special cases both Seidenfeld et al.'s (2010) choice functions on horse lotteries and sets of desirable gambles (Quaeghebeur, 2014), and to investigate their connections. We show that choice functions based on sets of desirable options (gambles) satisfy Seidenfeld's convexity axiom only for very particular types of sets of desirable options, which are in a one-to-one relationship with the lexicographic probabilities. We call them lexicographic choice functions. Finally, we prove that these choice functions can be used to determine the most conservative convex choice function associated with a given binary relation.

Desirability and the birth of incomplete preferences

We establish an equivalence between two seemingly different theories: one is the traditional axiomatisation of incomplete preferences on horse lotteries based on the mixture independence axiom; the other is the theory of desirable gambles developed in the context of imprecise probability. The equivalence allows us to revisit incomplete preferences from the viewpoint of desirability and through the derived notion of coherent lower previsions. On this basis, we obtain new results and insights: in particular, we show that the theory of incomplete preferences can be developed assuming only the existence of a worst act---no best act is needed---, and that a weakened Archimedean axiom suffices too; this axiom allows us also to address some controversy about the regularity assumption (that probabilities should be positive---they need not), which enables us also to deal with uncountable possibility spaces; we show that it is always possible to extend in a minimal way a preference relation to one with a worst act, and yet the resulting relation is never Archimedean, except in a trivial case; we show that the traditional notion of state independence coincides with the notion called strong independence in imprecise probability---this leads us to give much a weaker definition of state independence than the traditional one; we rework and uniform the notions of complete preferences, beliefs, values; we argue that Archimedeanity does not capture all the problems that can be modelled with sets of expected utilities and we provide a new notion that does precisely that. Perhaps most importantly, we argue throughout that desirability is a powerful and natural setting to model, and work with, incomplete preferences, even in case of non-Archimedean problems. This leads us to suggest that desirability, rather than preference, should be the primitive notion at the basis of decision-theoretic axiomatisations.

Irrelevant and independent natural extension for sets of desirable gambles

The results in this paper add useful tools to the theory of sets of desirable gambles, a growing toolbox for reasoning with partial probability assessments. We investigate how to combine a number of marginal coherent sets of desirable gambles into a joint set using the properties of epistemic irrelevance and independence. We provide formulas for the smallest such joint, called their independent natural extension, and study its main properties. The independent natural extension of maximal coherent sets of desirable gambles allows us to define the strong product of sets of desirable gambles. Finally, we explore an easy way to generalise these results to also apply for the conditional versions of epistemic irrelevance and independence. Having such a set of tools that are easily implemented in computer programs is clearly beneficial to fields, like AI, with a clear interest in coherent reasoning under uncertainty using general and robust uncertainty models that require no full specification.

Conservative Inference Rule for Uncertain Reasoning under Incompleteness

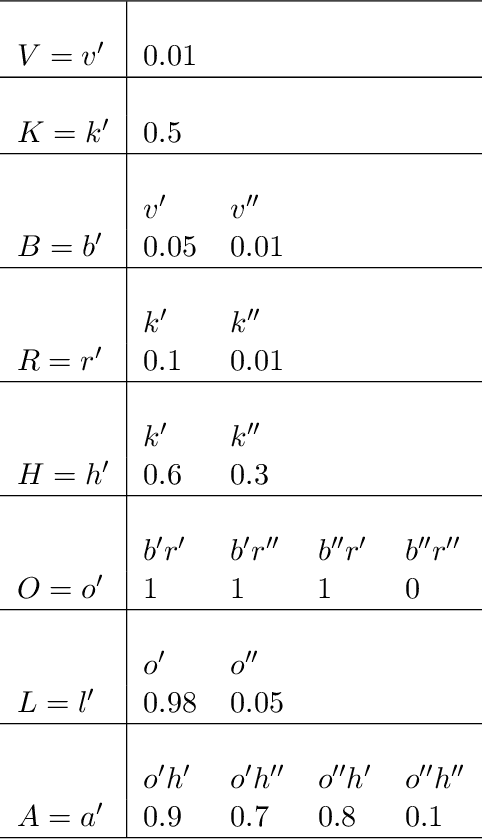
In this paper we formulate the problem of inference under incomplete information in very general terms. This includes modelling the process responsible for the incompleteness, which we call the incompleteness process. We allow the process behaviour to be partly unknown. Then we use Walleys theory of coherent lower previsions, a generalisation of the Bayesian theory to imprecision, to derive the rule to update beliefs under incompleteness that logically follows from our assumptions, and that we call conservative inference rule. This rule has some remarkable properties: it is an abstract rule to update beliefs that can be applied in any situation or domain; it gives us the opportunity to be neither too optimistic nor too pessimistic about the incompleteness process, which is a necessary condition to draw reliable while strong enough conclusions; and it is a coherent rule, in the sense that it cannot lead to inconsistencies. We give examples to show how the new rule can be applied in expert systems, in parametric statistical inference, and in pattern classification, and discuss more generally the view of incompleteness processes defended here as well as some of its consequences.