Intermittent time series forecasting: local vs global models

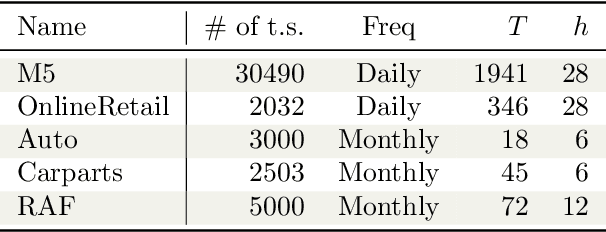
Intermittent time series, characterised by the presence of a significant amount of zeros, constitute a large percentage of inventory items in supply chain. Probabilistic forecasts are needed to plan the inventory levels; the predictive distribution should cover non-negative values, have a mass in zero and a long upper tail. Intermittent time series are commonly forecast using local models, which are trained individually on each time series. In the last years global models, which are trained on a large collection of time series, have become popular for time series forecasting. Global models are often based on neural networks. However, they have not yet been exhaustively tested on intermittent time series. We carry out the first study comparing state-of-the-art local (iETS, TweedieGP) and global models (D-Linear, DeepAR, Transformers) on intermittent time series. For neural networks models we consider three different distribution heads suitable for intermittent time series: negative binomial, hurdle-shifted negative binomial and Tweedie. We use, for the first time, the last two distribution heads with neural networks. We perform experiments on five large datasets comprising more than 40'000 real-world time series. Among neural networks D-Linear provides best accuracy; it also consistently outperforms the local models. Moreover, it has also low computational requirements. Transformers-based architectures are instead much more computationally demanding and less accurate. Among the distribution heads, the Tweedie provides the best estimates of the highest quantiles, while the negative binomial offers overall the best performance.

Forecasting intermittent time series with Gaussian Processes and Tweedie likelihood

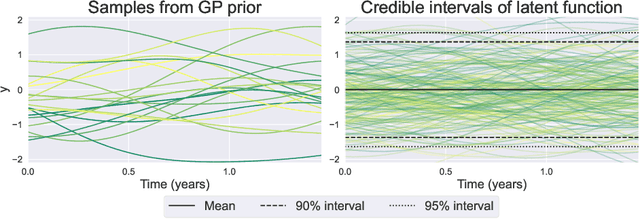
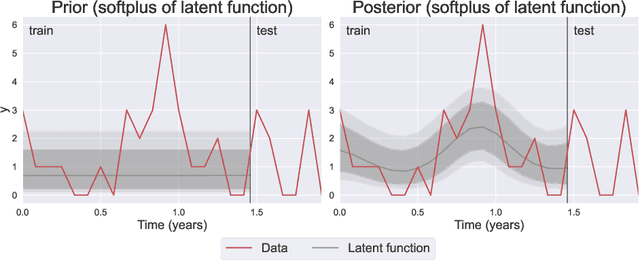
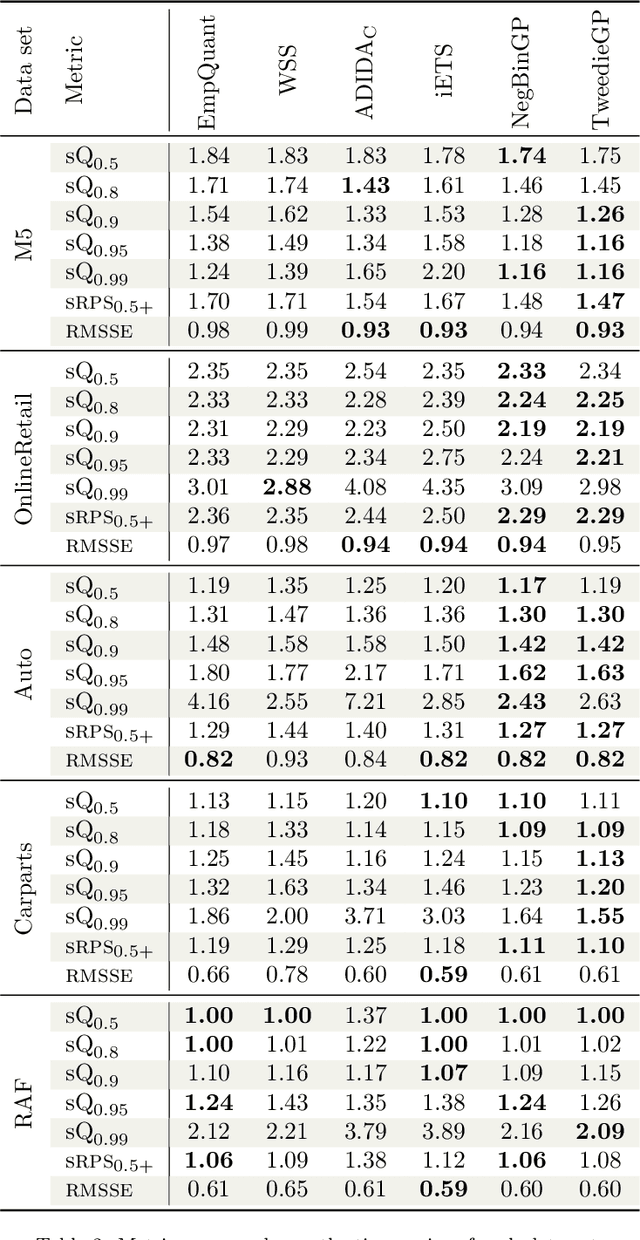
We introduce the use of Gaussian Processes (GPs) for the probabilistic forecasting of intermittent time series. The model is trained in a Bayesian framework that accounts for the uncertainty about the latent function and marginalizes it out when making predictions. We couple the latent GP variable with two types of forecast distributions: the negative binomial (NegBinGP) and the Tweedie distribution (TweedieGP). While the negative binomial has already been used in forecasting intermittent time series, this is the first time in which a fully parameterized Tweedie density is used for intermittent time series. We properly evaluate the Tweedie density, which is both zero-inflated and heavy tailed, avoiding simplifying assumptions made in existing models. We test our models on thousands of intermittent count time series. Results show that our models provide consistently better probabilistic forecasts than the competitors. In particular, TweedieGP obtains the best estimates of the highest quantiles, thus showing that it is more flexible than NegBinGP.