Causal-driven attribution (CDA): Estimating channel influence without user-level data

Attribution modelling lies at the heart of marketing effectiveness, yet most existing approaches depend on user-level path data, which are increasingly inaccessible due to privacy regulations and platform restrictions. This paper introduces a Causal-Driven Attribution (CDA) framework that infers channel influence using only aggregated impression-level data, avoiding any reliance on user identifiers or click-path tracking. CDA integrates temporal causal discovery (using PCMCI) with causal effect estimation via a Structural Causal Model to recover directional channel relationships and quantify their contributions to conversions. Using large-scale synthetic data designed to replicate real marketing dynamics, we show that CDA achieves an average relative RMSE of 9.50% when given the true causal graph, and 24.23% when using the predicted graph, demonstrating strong accuracy under correct structure and meaningful signal recovery even under structural uncertainty. CDA captures cross-channel interdependencies while providing interpretable, privacy-preserving attribution insights, offering a scalable and future-proof alternative to traditional path-based models.

Incorporating Expert Opinion on Observable Quantities into Statistical Models -- A General Framework

This article describes an approach to incorporate expert opinion on observable quantities through the use of a loss function which updates a prior belief as opposed to specifying parameters on the priors. Eliciting information on observable quantities allows experts to provide meaningful information on a quantity familiar to them, in contrast to elicitation on model parameters, which may be subject to interactions with other parameters or non-linear transformations before obtaining an observable quantity. The approach to incorporating expert opinion described in this paper is distinctive in that we do not specify a prior to match an expert's opinion on observed quantity, rather we obtain a posterior by updating the model parameters through a loss function. This loss function contains the observable quantity, expressed a function of the parameters, and is related to the expert's opinion which is typically operationalized as a statistical distribution. Parameters which generate observable quantities which are further from the expert's opinion incur a higher loss, allowing for the model parameters to be estimated based on their fidelity to both the data and expert opinion, with the relative strength determined by the number of observations and precision of the elicited belief. Including expert opinion in this fashion allows for a flexible specification of the opinion and in many situations is straightforward to implement with commonly used probabilistic programming software. We highlight this using three worked examples of varying model complexity including survival models, a multivariate normal distribution and a regression problem.

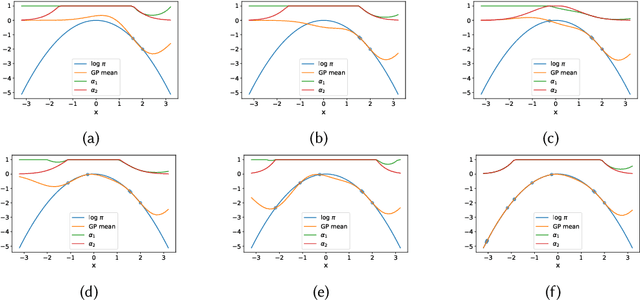
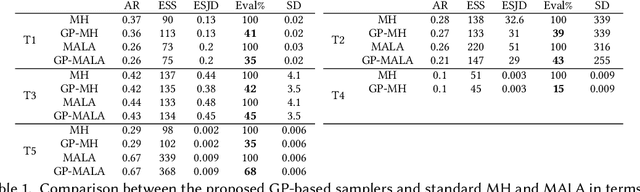
Gaussian Processes to speed up MCMC with automatic exploratory-exploitation effect

We present a two-stage Metropolis-Hastings algorithm for sampling probabilistic models, whose log-likelihood is computationally expensive to evaluate, by using a surrogate Gaussian Process (GP) model. The key feature of the approach, and the difference w.r.t. previous works, is the ability to learn the target distribution from scratch (while sampling), and so without the need of pre-training the GP. This is fundamental for automatic and inference in Probabilistic Programming Languages In particular, we present an alternative first stage acceptance scheme by marginalising out the GP distributed function, which makes the acceptance ratio explicitly dependent on the variance of the GP. This approach is extended to Metropolis-Adjusted Langevin algorithm (MALA).