Jason Wyse
Gaussian Processes to speed up MCMC with automatic exploratory-exploitation effect
Sep 28, 2021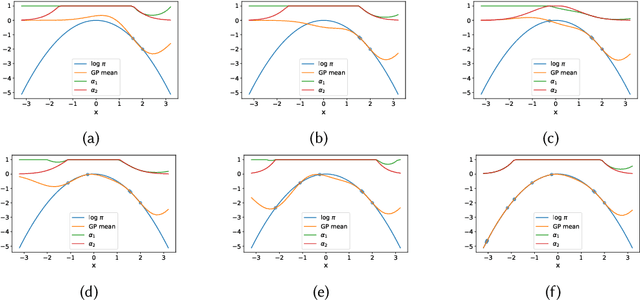
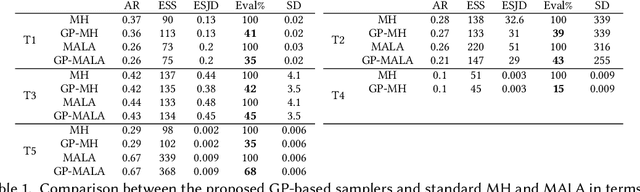
Abstract:We present a two-stage Metropolis-Hastings algorithm for sampling probabilistic models, whose log-likelihood is computationally expensive to evaluate, by using a surrogate Gaussian Process (GP) model. The key feature of the approach, and the difference w.r.t. previous works, is the ability to learn the target distribution from scratch (while sampling), and so without the need of pre-training the GP. This is fundamental for automatic and inference in Probabilistic Programming Languages In particular, we present an alternative first stage acceptance scheme by marginalising out the GP distributed function, which makes the acceptance ratio explicitly dependent on the variance of the GP. This approach is extended to Metropolis-Adjusted Langevin algorithm (MALA).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge